基于生态用水的Hargreaves模型修正
邱 微,樊庆锌,王明轩,韩文滔,彭雪璇
(1.哈尔滨工业大学市政环境工程学院,150090 哈尔滨;2.哈尔滨工业大学城市水资源与环境国家重点实验室,150090 哈尔滨)
基于生态用水的Hargreaves模型修正
邱 微1,2,樊庆锌1,王明轩1,韩文滔1,彭雪璇1
(1.哈尔滨工业大学市政环境工程学院,150090 哈尔滨;2.哈尔滨工业大学城市水资源与环境国家重点实验室,150090 哈尔滨)
生态需水量核算问题中,国内外常用的几种潜在蒸散量计算模型具有一定的限制性,为此,结合东北地区特点,以哈尔滨市为例,选取时间序列指标数据,对比分析常用计算模型的适用性及不足,提出修正并优化Hargreaves(HM)模型的方法并进行参数修定.修正后HM模型的计算结果与PM模型的相关系数达0.826,相对均方差为0.119,相关性较好,可满足哈尔滨市蒸散量的计算.
生态需水;HM模型;修正模型
水资源时空分布差异及人类活动对水环境的影响,使得水资源供需矛盾成为区域乃至全球性的突出问题.城市在现阶段发展过程中,有限的水资源优先用于工农业生产和城乡居民生活,导致生态用水缺失,进而造成许多生态环境问题.在水资源分配过程中,重视生态用水规划、保障生态用水安全具有重要现实意义.目前,国内生态用水的研究多采用国外推荐的模型进行核算.其中植被生态用水量作为河道外生态用水中比重最大的部分,确定植被生态用水的重要模型——潜在蒸散量模型也是由国外科学家确立.由于气候条件不同,用该模型计算我国北方地区潜在蒸散量时误差较大,需要对该用水量中的估算模型进行细致选择、改进和参数估计.
潜在蒸散量的计算方法有很多种,如水汽扩散法、能量平衡法、布德柯综合法、Penman-Monteith模型(PM)、Thornthwaite模型(TM)和Hargreaves模型(HM)等.国外对于Hargreaves模型的参数研究较多,如 F.Bautista和 D.Bautista[1]对 Hargreaves模型中的常数 0.002 3 进行了修改,使其符合Yucatán地区的特点.国内一些学者也对Hargreaves公式在中国的应用进行了详细研究,并修正Hargreaves公式,提出了适合研究区域气候条件的植物蒸散量计算模型[2].胡庆芳等[3]以 Hargreaves模型 为基 础,提 出 了Hargreaves模型的全局校正方法,并对其适用性进行了评价;刘晓英等[4]依据华北地区6个气象站的观测资料,研究了3种基于温度的潜在蒸散量ETO计算方法;赵永等[5]利用HM与PM的相关性,对Hargreaves模型进行了修正,并通过山西省的历史气象数据进行验证.薛银民[6]研究了气象资料匮乏地区的参考作物需水量的核算方法.为了研究Hargreaves模型在哈尔滨地区的适用性,获得较精确的结果,对Hargreaves模型进行校正,对参数Ci按每月进行率定,提高HM公式在北方地区计算的准确性及适用性.
1 常用潜在蒸散量模型
植被的生态用水量可看作是植被枝叶和土壤实际蒸散量的总和,即植被耗水量.计算植被生态用水量的前提是计算植被生态用水定额,即单位时间单位面积植被的用水量.计算植被生态用水定额中最常用的方法是先用气象因素计算参考作物潜在蒸散量,根据潜在蒸散量乘以适当的系数求算植被耗水定额.
1.1 Penman-Monteith(PM)模型
联合国粮农组织(FAO)认为Penman-Monteith模型是计算潜在蒸散量最有效、可靠的方法.Penman-Monteith模型考虑了植被生理特征,且以能量平衡和水汽扩散理论为基础建立[7-10],并经过大量的实例验证,计算出的潜在蒸散量与实际值最接近[11-13].由于多数地区缺少实测 ETO资料,联合国粮农组织在1998年将PM法作参考标准检验其他经验公式的有效性[14].但是PM法需要4种气象参数(计算时段内的平均温度、相对湿度、风速和平均日照时数[15])完成计算,这些参数很难获取,且计算过程较复杂,效率低.
Penman-Monteith模型如下:
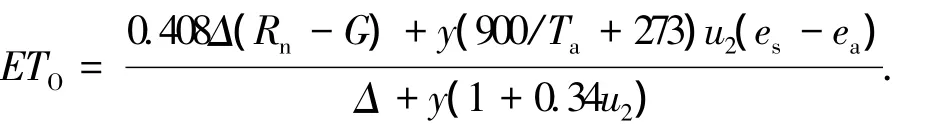
式中:ETO为潜在蒸散量(mm/d);Δ为饱和水气压与温度曲线斜率(kPa/℃);Rn为每日净辐射(MJ/(m2·d));G为土壤热通量(MJ/(m2·d));y为干湿表常数(kPa/℃);Ta为2 m高度处的日平均气温(℃);u2为2 m高度处的风速(m/s);es为饱和水气压(kPa);ea为实际水气压(kPa).
1.2 Thornthwaite(TM)模型
Thornthwaite法是 C.W.Thornthwaite在 1948年根据美国中东部地区的气象实验数据提出的[16].在美国,TM 法广泛应用并得到好评.该方法不仅用在植被潜在蒸散量的计算上,还应用于植被-气候分类中.Thornthwaite法涉及的参数只有月平均温度,将潜在蒸散量ETO视为月平均温度的幂函数,即


1.3 Hargreaves(HM)模型
Hargreaves和Samani在20世纪50年代提出了Hargreaves(HM)模型,并不断完善.Hargreaves模型涉及的气象参数包括每日最低温度、每日最高温度、每日平均气温及大气层顶辐射.比PM公式简单很多[16-19],模型如下:
ETO=0.002 3(Tmed+17.78)(Tmax- Tmin)0.5Ra.式中:ETO为潜在蒸散量(mm/d);Ci=0.002 3,为校正参数;Tmin、Tmax、Tmed为每日最低温度、每日最高温度、每日平均气温(℃);Ra为大气层顶辐射(以水量计)(mm/d),可根据FAO公式计算或文献[14]得到.
2 各模型蒸散量计算与分析
各计算模型所需参数如下:土地热通量、干湿表常数、饱和水气压、平均温度、饱和水气压与温度的斜率、平均净辐射量、平均风速、实际水气压、最高温度、最低温度、大气层顶辐射,以哈尔滨为例收集原始数据.依据上述模型及相关参数原始数据,对哈尔滨市2004~2008年间4~10月潜在蒸散量进行核算,结果见图1.

图1 3种模型计算结果对比
由图1可知:
1)TM法计算出的潜在蒸散量与作为参考标准的PM法的结果相差很大,原因为:
①TM公式中只考虑了温度对ETO的影响,没有考虑另一主要影响因素辐射值;
②TM公式最初建立时是基于美国东部当地的气象数据,对于其他地区的适应性较差,公式中涉及的月热量指数h和A的线性回归均应根据不同地区进行相应的率定.
由此判定TM公式不适于我国北方哈尔滨地区潜在蒸散量的计算.
2)HM公式计算的潜在蒸散量与参考标准PM法的结果较相近,但仍存在一定偏差,主要是由地域的差异引起的.由于Hargreaves公式建立的基础资料来自美国西北部较干旱地区,该公式仅在类似地区具有较强应用价值,在我国北方地区的应用存在一些问题.为提高HM公式在北方地区计算的准确性及适用性,对其公式中的参数Ci按每月进行率定,使其符合哈尔滨地区的特点,进而确定与研究地域相适应的计算模型,使其更科学、高效、准确.
3 Hargreaves模型的校正及优化
3.1 Hargreaves模型的校正
Hargreaves模型经过了不断的校正.1975年,美国科学家Hargreaves在计算加州Davis地区某种草类作物的潜在蒸散量时,提出了如下公式:

式中,TC=(Tmax+Tmin)/2.但是当时Hargreaves尚未提出 Rs的具体计算公式.直到 1977年,Hargreaves提出了一个计算Rs的经验公式,Rs=0.075RaS0.5,S为实测日照时数与可能日照时数的比.由于许多地区缺乏实测的日照时数,计算S比较困难,该式仍不能广泛使用.1983年,Hargreaves根据Senegal的气象资料,对其进一步改正,即

Hargreaves公式能够利用较易获得的气象资料准确地估算ETO,应用较普遍.但根据其建立的机理及过程可知,公式中的校正项,即参数Ci=0.002 3的确定,是Hargreaves1985年在加利福尼亚Davis地区基于苇状羊茅草的潜在蒸散量,经回归后计算所得,因此,Ci值只适用于Davis地区的计算.如果直接用于其他地区可能出现较大偏差,尤其是在干旱、炎热地区应用时需要进行修正[20-21].
为了研究Hargreaves模型在哈尔滨地区的适用性,获得较精确的结果,对Hargreaves模型进行校正.由于一年中各月份的降水量、日照时间、温度等气候因素差异明显,不同月份中模型参数Ci应该取不同值,从而保证Hargreaves公式的计算结果最大限度地接近真实的潜在蒸散量.对于参数的确定,将相关历史数据分为两部分,一部分作为训练集,用于求出各月份对应的参数Ci;另一部分用于对所求的参数进行验证,检验其准确性.通过与PM计算结果进行对比,找出最适合哈尔滨市典型东北气候下的Hargreaves模型.
基于Bautista等[1]在计算墨西哥某城市潜在蒸散量的思想,将PM公式计算出的潜在蒸散量作为参考标准,采用修正Hargreaves模型中常系数0.002 3的方法.
由Hargreaves公式得
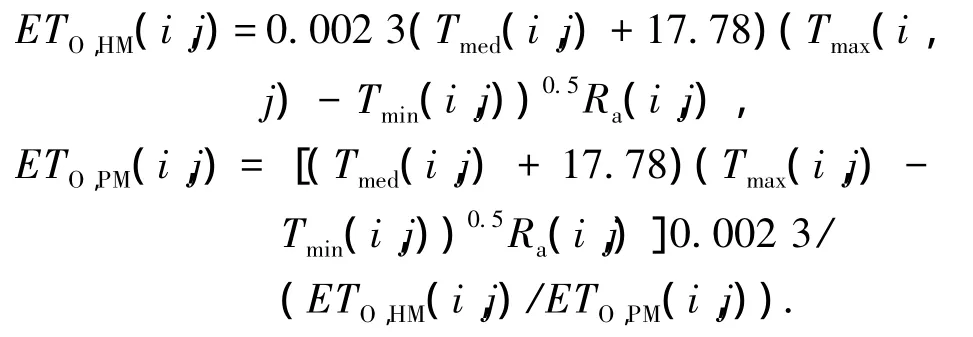
通过5年同一月份PM计算的ETO均值和HM计算的ETO值的均值做商,确定每月调整后的参数 Ciadj.即
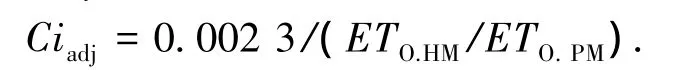
式中:Ciadj为Hargreaves公式中修正后的参数;(i,j)为第j年的i月份,i=1 ~12,j=2004 ~2008;ETO,HM为Hargreaves公式得出的每月潜在蒸散量;ETO,PM为Penman-Monteith公式计算出的每月潜在蒸散量.
以2004~2008年的月平均气象参数为训练集进行参数率定,结果见表1.

表1 校正后Ciadj结果
与参考标准PM的计算结果进行对比,判断模型修正的准确性.首先检查修正后的HM计算值与PM计算值的相关性,对两者进行线性回归,通过建立散点图与回归曲线及其相关系数,判断两者之间的相关性.结果见图2.可以看出,将2004~2008年4~10月共35个修正后的HM计算值与PM计算值作回归,得R2=0.567,且两者之间的相关性较差.因此,该常数的修正方法应用于哈尔滨地区时,模型精度较差,与PM的计算结果相差大.

图2 修正后的HM计算值与PM计算值的相关性
为进一步验证修正公式的适用性与准确性,分别用PM公式与修正后的HM公式求得2009年4~10月潜在蒸散量,做其时序曲线,结果见图3.可以看出,两曲线的的总体趋势相一致,但在某些月份差别明显;通过计算,其相对均方误差(RMSE)为0.403,总体拟合效果不理想.

图3 修正后的HM计算的潜在蒸散量与PM的比较
3.2 Hargreaves修正模型的优化
通过上述分析可知,F.Bautista和 D.Bautista提出的模型参数修正方法,应用于本研究地域哈尔滨地区结果不理想,计算值与标准值之间的相对均方误差较大,且相关性不高,体现不了Hargreaves公式在哈尔滨地区的适用性.通过研究其修正方法和机理,发现在通过Hargreaves公式计算ETO,HM值时,所有变量的取值均为同一月份5年的平均值,PM与HM的取值也均为相应月份5年的平均值.如果将均值引入原始的计算式中,无法体现不同年份之间的变化,使得计算精确度下降.因此,认为对于公式中参数Ci的修订,应用原始公式分别计算同一月份5年中不同的潜在蒸散量(包括HM与PM),取同一月份各年HM与PM的比值再进行平均,这样可避免其精确度下降,即

式中:Ciadj为Hargreaves公式中校正后的常数项;(i,j)为第j年的i月份,i=1 ~12,j=2001 ~2005;ETO,HM为Hargreaves公式得出的每月潜在蒸散量;ETO,PM为Penman-Monteith公式计算出的每月潜在蒸散量.
基于本文提出的HM模型参数修正方法的计算结果见表2.

表2 新校正后Ciadj结果
同样采用2004~2008年的数据计算,并由线性回归判断两者相关性,结果见图4.可以看出,通过本文提出的模型修正方法进行参数的修定后,其计算值与PM计算值相关性较强,相关系数达0.826,说明修正后HM的计算结果与PM的结果相关性较好,可基本满足对哈尔滨市蒸散量的计算.

图4 新修正后的HM计算值与PM计算值的相关性
为进一步验证此方法修正后模型的准确性,通过PM和HM计算的2009年潜在蒸散量时序图(图5)可知,两条曲线非常接近,拟合程度很好,其相对均方误差RMSE=0.119,说明误差可以接受,结果满意.

图5 PM与新法修正后的HM计算潜在蒸散量的比较
由此可知,本文提出的新HM模型参数修定方法更适合东北地区潜在蒸散量的计算.
4 结 论
1)根据哈尔滨市2004~2008年4~10月的时间序列数据,通过对联合国粮农组织推荐的3种植被潜在蒸散量模型的计算,分析TM模型和PM模型不适用于东北地区的原因.
2)分析HM模型的构建和修正过程,对模型参数Ci按每月进行率定,针对哈尔滨地区计算数据进行模型修正,并根据计算结果进行模型优化.
3)按本研究提出的HM模型修正方法进行参数修定后,其计算值与PM计算值相关性较强,相关系数达0.826,说明修正后HM模型可基本满足对哈尔滨市蒸散量的计算.
4)以哈尔滨市为代表,建立了适用于东北地区植被生态用水计算的模型,为下一阶段选择小范围时间尺度(如周、天)、长时间序列数据,开展定量核算哈尔滨市生态需水问题奠定基础.
[1]BAUTISTA F,BAUTISTA D,DELGADO-CARRANZA C.Calibration ofthe equations ofhargreaves and thornthwaite to estimate the potential evapotranspiration in semi-arid and subhumid tropical climates for regional applications[J].ATMOSFERA,2009,22(4):331-348.
[2]云文丽,侯琼,王永利,等.内蒙古典型草原作物系数和实际蒸散量的时空分布特征[J].自然资源学报,2013,28(2):300-311.
[3]胡庆芳,杨大文,王银堂,等.Hargreaves公式的全局校正及适用性评价[J].水科学进展,2011,22(2):160-167.
[4]刘晓英,李玉中,王庆锁.几种基于温度的参考作物蒸散量计算方法的评价[J].农业工程学报,2006,22:12-18.
[5]赵永,蔡焕杰,王健,等.Hargreaves计算参考作物蒸发蒸腾量公式经验系数的确定[J].干旱地区农业研究,2004,22(4):44-47.
[6]薛银民.气象资料匮乏地区参考作物需水量的一种简化算法[J].水电能源科学,2013,31(2):30-31.
[7]TORRES A F,WALKER W R,KEE M M.Forecasting daily potential evapotranspiration using machine learning and limited climaticdata[J].AgriculturalWater Management,2011,98(4):553-562.
[8]RIVAS R,CASELLES V.A simplified equation to estimate spatialreference evaporation from remote sensing-based surface temperature and local meteorological data[J]. Remote Sensing of Environment,2004,93(1/2):68-76.
[9]RAZIEI T,PEREIRA L S.Estimation of ETOwith Hargreaves-Samani and FAO-PM temperature methods for a wide range of climates in Iran[J].Agricultural Water Management,2013,121:1-18.
[10]SILVA D,MEZA F J,VARAS E.Estimating reference evapotranspiration(ETO)using numericalweather forecast data in central Chile[J].Journal of Hydrology,2010,382(1/2/3/4):64-71.
[11]POLHAMUS A,FISHER J B,TU K P.What controls the error structure in evapotranspiration models?[J].Agricultural and Forest Meteorology,2013,169:12-24.
[12]PENMAN H L.Vegetation and hydrology[M].England Harpenden:Commonwealth Bureau of Soils,1963:125.
[13]陈莉,方丽娟,李帅.东北地区生长季潜在蒸散量的变化特征分析[J].灾害学,2010,25(2):92-96.
[14]ALLEN R,PEREIRA L S,RAES D,et al.Crop evapotranspiration:guidelines for computing crop water requirements[J].FAO Irrigation and Drainage,1998,56:290-300.
[15]BORNN L,ZIDEK J V.Efficient stabilization of crop yield prediction in the Canadian Prairies[J].Agricultural and Forest Meteorology,2012,152:223-232.
[16]THORNTHWAITE C W.An approach toward a rational classification of climate [J].Geography Rev,1948,5:38.
[17]HARGREAVES G L,RILEY J P.Agricultural benefits for senegal river basin[J].Journal of Irrigation and Drainage Engneering,1985,111:113-124.
[18]TODOROVIC M,KARIC B,PEREIRA L S.Reference evapotranspiration estimate with limited weather data across a range of mediterranean climates[J].Journal of Hydrology,2013,481:166-176.
[19]DAUT I,IRWANTO M,IRWAN Y M, et al.Combination of Hargreaves method and linear regression as a new method to estimate solar radiation in Perlis,Northern Malaysia[J].Solar Energy,2011,85(11):2871-2880.
[20]TRAJKOVIC S.Temperature-based approaches for estimating reference evapotranspiration[J].Journal of Irrigation and Drainage Engineering,2005,131(4):316-323.
[21]COBANER M.Evapotranspiration estimation by two different neuro-fuzzy inference systems[J].Journal of Hydrology,2011,398(3/4):292-302.
Amending the Hargreaves model based on ecological water
QIU Wei1,2,FAN Qingxin1,WANG Mingxuan1,HAN Wentao1,PENG Xuexuan1
(1.School of Municipal and Environmental Engineering,Harbin Institute of Technology,150090 Harbin,China;2.State Key Laboratory of Urban Water Resource and Environment,Harbin Institute of Technology,150090 Harbin,China)
Many researches focus on the ecological water demand accounting problem.But it has a certain restriction of several potential evapotranspiration models commonly used in China and abroad.Combined with the northeast area characteristic,the paper has chosen Harbin as the example.It has selected a series time of indicator data and compared the applicability and disadvantage about these models.The paper proposes the method to amend and optimize the Hargreaves(HM)model.It also revised the parameters.The correlation coefficient of amending HM and the PM calculations is 0.826,and the relative mean squared deviation is 0.119.It has a good correlation of calculating the evapotranspiration calculation of Harbin.And it will lay the foundation for the quantitative accounting ecological water demand of the northeast region.
ecological water demand;Hargreaves model modification;amend model
X37
A
0367-6234(2014)02-0021-05
2013-03-20.
国家自然科学基金资助项目(51208143);中央高校基本科研业务费专项资金资助项目 (HIT.NSRIF.2012086);城市水资源与水环境国家重点实验室自主课题(哈尔滨工业大学)(2012TS03);黑龙江省博士后科研启动金资助项目(LBH-Q12074,LBHQ12002).
邱 微(1980—),女,博士,副教授.
樊庆锌,fanqingxin@hit.edu.cn.
(编辑 刘 彤)

