基于BDNM的桥梁结构可靠度预测

樊学平，吕大刚

(哈尔滨工业大学土木工程学院，150090 哈尔滨)

基于BDNM的桥梁结构可靠度预测

樊学平，吕大刚

(哈尔滨工业大学土木工程学院，150090 哈尔滨)

为了结合监测极值应力和应力参数(平均值)的先验模型来对桥梁可靠度进行预测，认为极值应力随时间变化的动态测量为一个时间序列，并考虑到贝叶斯动态线性模型(BDLM)的局限性，引入贝叶斯动态非线性模型(BDNM)对时变极值应力进行预测.运用BDNM建立了极值应力的状态方程和监测方程，通过泰勒级数展开技术，将其近似转化为贝叶斯动态线性模型(BDLM)，并通过贝叶斯因子来对应力信息进行监控，然后结合应力参数的先验信息，对极值应力的状态参数进行贝叶斯后验概率推断，建立动态模型对极值应力变化趋势进行预测.基于监测信息，考虑到变量估计主观认识的不确定性，引入折扣因子来确定状态误差方差.最后利用建立的BDNM和一次二阶矩(FOSM)可靠度方法，对结构可靠度进行预测，并通过实例验证了所建模型的合理性和适用性.

桥梁健康监测;应力;贝叶斯动态非线性模型;贝叶斯动态线性模型;可靠度预测

桥梁健康监测大致分为两个阶段［1-2］，第一个阶段为健康监测系统的研制与开发，包括传感器的研发和应用、数据无线传输系统的研发、数据采集与系统集成技术等，目前已处于成熟阶段［3-4］;第二个阶段为健康监测信息的应用，大量研究主要集中在模态参数识别、损伤识别、模型修正等领域［5］，而在桥梁结构的可靠度预测和评定方面，虽然已取得了一定成果［6-8］，但是基于桥梁结构的健康监测信息对结构的可靠度进行实时预测和评定，在国内外还处于研究起步阶段.作为贝叶斯预测模型中最重要的一类模型，贝叶斯动态线性模型(BDLM)在大坝数据监测［9］、地基沉降数据预测［10］、混凝土结构性能预测［11-13］等领域已得到应用，但此模型在桥梁结构的健康监测领域还未得到广泛应用.因而本文尝试基于桥梁结构健康监测信息，建立基于监测极值应力的贝叶斯动态非线性模型，通过非线性函数的近似线性化［14-15］，将监测极值应力的贝叶斯动态非线性模型近似转化为贝叶斯动态线性模型，然后基于建立的贝叶斯动态线性模型，对桥梁结构的可靠度进行离线实时预测，最后通过工程实例验证所建模型的合理性.

1 桥梁监测极值应力的BDNM

健康监测系统在结构长期运营中，可采集大量数据信息，本文主要利用监测的极值应力信息，即监测系统每天采集的应力数据的极大值θt表示状态变量，即监测应力极值的平均值(趋势项数据);yt表示监测变量，即实时监测的应力极值.

1.1 BDNM的假定

文中建立的 BDNM假设:1)状态变量(θt)的变化是马尔科夫链［16］，且 θt与 θt-1呈非线性关系;2)观测变量(yt)是相互独立的，且yt只与状态变量θt相关，yt与θt呈线性关系.

状态变量与监测变量的递推关系见图1.

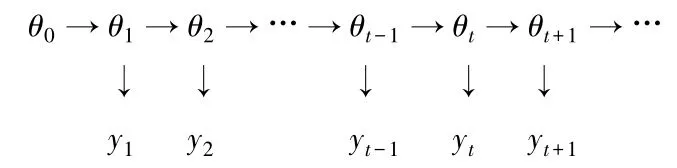
图1 状态空间模型的相关结构

1.2 BDNM的建立

贝叶斯动态模型主要由监测方程和状态方程组成.由于桥梁健康监测信息的复杂性，本文采用每天的监测应力极值来反映结构的应力状态.即主要通过建立监测应力极值的状态方程和监测方程，实现监测应力极值的预测.

本文建立的桥梁监测应力极值非线性动态预测模型为

1)监测方程

2)状态方程

3)初始先验信息(t-1时刻的信息)

式中:yt为t时刻系统的监测应力极值;νt为监测误差项;θt为t时刻的状态变量(监测极值应力的平均值或趋势项);ωt为状态噪声项;Vt和Wt分别为t时刻系统监测误差和状态噪声的方差;gt(·)为状态函数，且为非线性函数，它的物理意义是由应力极值随时间的变化呈非线性变化，可以推出结构应力极值的状态参数(极值应力的趋势项数据或平均值)的变化亦呈现非线性［17］;Dt为t时刻以及t时刻以前的信息集，且Dt={yt，Dt-1}，Dt-1为t-1时刻以及t-1时刻以前的信息集，mt-1为t-1时刻状态参数的平均值，Ct-1为t-1时刻状态参数的方差;此外，假设 νt、ωt相互独立，且都与.θt独立.

2 BDNM到BDLM的转化与递推

2.1 非线性模型的线性化

根据桥梁的健康监测信息，拟合出监测极值应力信息的变化趋势曲线h(t)(二次曲线)，此变化曲线近似作为状态变量的变化曲线:

由于结构状态变量的不可观测性，即式(4)的非线性，因而本文把监测极值应力的趋势曲线作为结构状态变量的变化曲线.采用泰勒级数展开技术，可以将非线性状态方程式(4)线性化为

式中h'(t)为h(t)在t时刻的斜率或一阶差分.

将应力极值的贝叶斯动态非线性预测模型基于泰勒级数展开进行线性化，应力的变化趋势一致，经本文作者研究变化所导致的相对误差不超过5%，足以满足实际工程的应用.由文献［18］可知，监测应力极值可近似服从正态分布，因而可直接运用FOSM方法进行可靠度计算.

2.2 BDNM到BDLM的转化

桥梁监测应力极值的近似动态线性模型为

1)监测方程

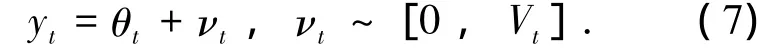
2)状态方程

3)初始先验信息

式中:h'(·)为状态函数在信息集Dt-1上的变化率，mt-1、Ct-1可以通过信息集Dt-1近似统计得到.

本文模型时间间隔长度取为1 d，Vt根据监测应力极值信息的样本方差进行估计;由文献［11，19］可知 Wt=-Ct-1+Ct-1/δ，式中 δ为折扣因子，根据经验一般取0.95 ～ 0.98.

2.3 BDLM的概率递推

BDLM适用于正态分布的概率递推，因而如果状态变量服从非正态分布，那么首先要将状态变量通过近似方法转化为正态分布［11］，递推过程如下:

1)t-1时刻的后验分布

对于均值mt-1和方差Ct-1，有

2)t时刻的先验分布

式中 at=mt-1，Rt=Ct-1+Wt.

3)t时刻一步预测分布

式中:ft=E(yt|Dt-1)=at，Qt=var(yt|Dt-1)=Rt+Vt，1/Qt为一步预测精度.

根据HPD区域的定义［14-15］，对于一步预测值的预测区间(95%的保证率)为

4)t时刻的后验分布

2.4 动态模型拟合优度的检验

本文通过一步预测的方差和贝叶斯因子的变化曲线来对预测模型的拟合优度进行检验.

经过预测方差曲线可以得知预测精度的变化规律，而贝叶斯因子的变化规律可以体现动态模型实时预测精度的优劣.

具体检验准则如下:预测精度随时间越来越大，则模型合理.

贝叶斯因子γ(t+1，t)反映了t+1时刻和t时刻模型对系统拟合的对比情况.若γ(t+1，t)≥1或者更大，则说明模型对于系统的拟合越来越好.

贝叶斯因子［14-15，20-21］的表达式为

式中:γ为动态贝叶斯因子;p(xt+1|Dt)为t时刻的一步预测概率密度函数在 xt+1处的值;p(xt|Dt-1)为t-1时刻的一步预测概率密度函数在xt处的值.

由于该因子的分子和分母都是监测应力极值的边际密度，因此γ(t+1，t)反映了在t+1时刻和t时刻模型对系统拟合的对比情况.

3 桥梁结构的可靠度预测

3.1 一次二阶矩方法(FOSM)

本文采用一次二阶矩方法(FOSM)［22］预测桥梁结构或构件的可靠指标，即只考虑预测信息或监测应力极值信息的平均值和标准差.

假设随机变量R(广义抗力)和S(广义荷载效应)相互独立，其平均值和标准差分别为:μR，

广义的极限状态方程为

可靠指标按下式计算:

3.2 可靠度预测公式

本文所研究桥梁结构［20］的极限状态方程为

式中:R为钢材屈服强度，S为钢材自重产生的应力，C为混凝土自重产生的应力，M为实时监测或预测的极值应力，γM为传感器系数.

基于3.1节提到的FOSM，本文给出桥梁结构的可靠度预测公式为

式中:μM和σM分别为通过BDNM递推得到的一步预测平均值与标准差;μR和σR分别为按照规范计算的抗力的均值和标准差;μS和σS分别为由钢板恒载所引起的应力的均值和标准差;μC和σC分别为由混凝土恒载所引起的应力的均值和标准差;γP是传感器的修正系数.

式(16)中的广义抗力R的统计参数(μR，σR)对应式(18)的按规范计算所得的抗力的平均值和标准差(μR，σR);广义荷载效应S的统计参数(μS，σS)包括三部分:1)钢板恒载所引起的应力的均值和标准差;2)混凝土恒载所引起的应力的均值和标准差;3)贝叶斯动态模型递推得到的活荷载效应的一步预测平均值与标准差.

4 实例验证

某桥建于1961年，此桥为一座五跨连续钢板梁桥［12，18，23-24］，全长 188.81 m，具体的桥梁工程资料及监测资料见参考文献［18，23］.对第二跨跨中边梁梁底的极值应力(CH15传感器采集到的信号)进行了40 d的监测，结构可靠指标的阈值为4.2.日常监测极值数据见表1.

表1 实时监测极值数据(工作荷载造成的应力)

算例中钢板梁桥的基本设计资料为

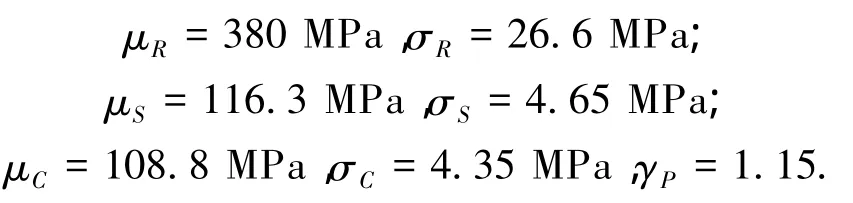
基于上述实时监测极值数据和基本设计资料，结合式(18)可得

4.1 拟合的应力变化趋势曲线

为了得到监测信息的趋势项数据信息，对监测极值数据进行曲线拟合和线性拟合;并经过拟合误差分析，发现二次曲线拟合比线性拟合的精度高，因而本文采用二次拟合曲线近似作为监测极值的状态曲线.

二次曲线拟合方程为

S(t)=-0.005 951t2+0.259 5t+23.48，状态函数在信息集Dt-1上的变化率为

4.2 基于二次曲线拟合方程的动态线性模型

根据2.2节可得到近似的动态线性模型为

监测方程 yt=mt+ νt，νt～ N［0，V］;

状态方程mt=mt-1+S't-1+ωt，

ωt～ N［0，Wt］;

先验信息(mt-1|Dt-1)～f(x).

式中:yt为t时刻极值应力的监测数据;mt为t时刻极值应力的趋势项值;S't-1为状态函数在信息集Dt-1上的变化率;νt为监测误差;ωt-1为状态误差，表示状态的不确定性.V可由以前大量的监测信息来确定，且Wt=-Ct-1+Ct-1/δ(根据工程经验取折扣因子为δ=0.98).

根据以前的监测应力极值资料以及设计资料可得状态变量服从对数正态分布，即f(x)为对数正态分布，分布参数为:平均值μ=25.5 MPa，变异系数为0.186.基于上述动态线性模型计算所得的监测应力极值和可靠度预测结果以及预测精度见图2～5.图2表示的是预测曲线与实时监测曲线的对比，由图2可知:监测应力的一步预测平均值的变化趋势与实时监测应力的变化趋势一样.由图3可知:随着监测应力的不断修正，一步预测精度越来越好.由图4可知:随着监测应力的修正，贝叶斯因子不断地接近于1，说明动态模型的拟合优度较好.由图5可知:随着监测信息的修正，本文得到的可靠度指标比Frangopol［18］得到的可靠指标小，主要由于本文考虑了监测极值应力的不确定性或随机性.

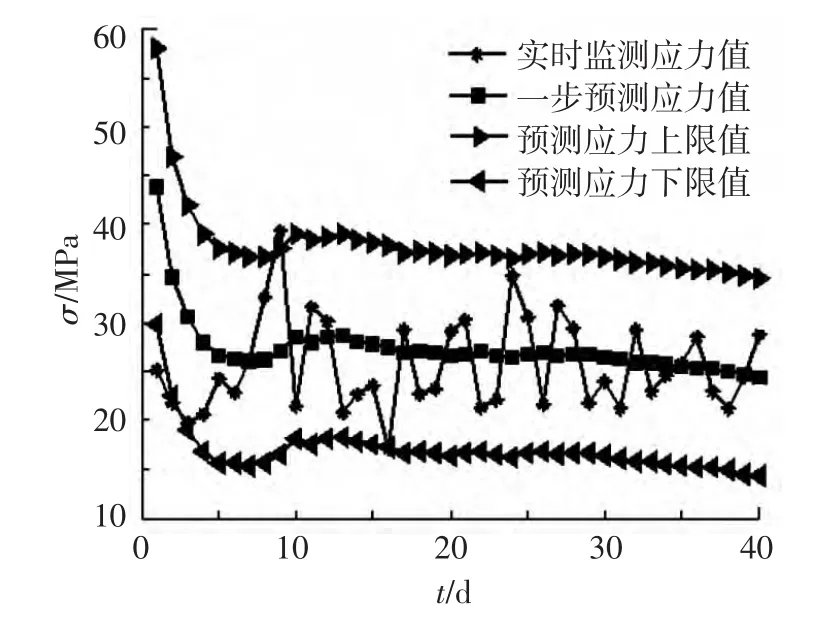
图2 基于贝叶斯动态模型的监测应力极值预测曲线

图3 预测精度的变化曲线

图4 贝叶斯因子的变化曲线

图5 可靠指标的变化曲线

5 结 论

1)建立了监测极值应力的贝叶斯动态非线性预测模型，并近似转化为贝叶斯动态线性模型，经分析可得:一步预测方差越来越小，即预测精度越来越高.贝叶斯因子随着时间的变化几乎接近于1，说明建立的动态模型对系统的拟合较好.

2)对结构的可靠度进行了预测研究，相对于确定性(方差为0)的监测极值应力的可靠指标而言，本文考虑了监测应力的随机性和不确定性，所得的可靠度较小，可以更好地对结构的安全状态进行预测评定.

3)本文尝试建立了少量离线监测数据的贝叶斯动态非线性模型，而基于较复杂的结构形式以及大量的的数据信息，建立合理的状态方程和监测机制有待进一步研究.

［1］樊学平，吕大刚.基于多个BDLM的桥梁结构可靠度实时预测［J］.华南理工大学学报，2013，41(3):70-75.

［2］樊学平，吕大刚.基于贝叶斯动态模型和非均匀采样的桥梁结构可靠度预测［C］//第22届全国结构工程学术会议.乌鲁木齐:新疆大学，2013:Ⅲ357-Ⅲ362.

［3］李惠，周文松，欧进萍，等.大型桥梁结构智能健康监测系统集成技术研究［J］.土木工程学报，2006，39(2):46-52.

［4］李爱群，缪长青，李兆霞，等.润扬长江大桥结构健康监测系统研究［J］.东南大学学报，2003，33(5):544-548.

［5］秦权.桥梁结构的健康监测［J］.中国公路学报，2000，13(2):37-42.

［6］李星新，汪正兴，王天亮，等.考虑目标可靠指标时变的既有桥梁动态可靠度评估［J］.桥梁建设，2007(增刊1):132-134.

［7］郭彤，李爱群，卞朝东.基于蒙特卡洛数值模拟的大跨桥梁状态评估［J］.公路交通科技，2005，22(8):26-30.

［8］杨跃新.混凝土连续梁桥的时变可靠度评定与寿命预测［D］.哈尔滨:哈尔滨工业大学，2007.

［9］汪树玉，刘国华，刘立军，等.大坝监测分析中的贝叶斯动态模型［J］.水利学报，1998(7):1-5.

［10］魏冠军，党亚民，章传银.应用贝叶斯动态模型的地基沉降概率分析与预测［J］.测绘科学，2012，37(2):52-53.

［11］王剑.基于信息更新的混凝土结构性能预测和可靠性管理［D］.北京:清华大学，2006.

［12］樊学平.基于实时监测信息的混凝土连续梁桥时变可靠度评定［D］.哈尔滨:哈尔滨工业大学，2010.

［13］樊学平，吕大刚.基于DLM的桥梁结构承载力的贝叶斯预测［J］.哈尔滨工业大学学报，2012，44(12):13-17.

［14］WEST M，HARRISON P J.Bayesian forecasting and dynamic models［M］.2nd ed.New York:Springer-Verlag，1998.

［15］WEST M，HARRISON J.Bayesian forecasting and dynamic models［M］.New York:Springer Verlag，1989.

［16］严甜.基于MDP的桥梁结构全寿命成本研究［D］.哈尔滨:哈尔滨工业大学，2010.

［17］CATBAS F N，SUSOY M，FRANGOPOL D M.Structural health monitoring and reliability estimation:Long span truss bridge application with environmental monitoring data［J］.Engineering Structures，2008，30:2347-2359.

［18］FRANGOPOL D M，STRAUSS A，KIM S.Use of monitoring extreme data for the performance prediction of structures:general approach ［J］. Engineering Structures，2008，30:3644-3653.

［19］GAO L F，LIU F S.The monitoring of Bayesian dynamic linear models without normal assumptions［J］.Journal of Mathematics，2005，25(3):245-248.

［20］苏兵.贝叶斯动态模型的模拟处理［D］.济南:山东大学，2007.

［21］PETRIS G，PETRONE S，CAMPAGNOLI P.Dynamic linear models with R［M］.New York:Springer Series，2009.

［22］MELCHERS R E.Structural reliability analysis and prediction［M］.2nd ed.Chichester:John Wiley ＆ Sons，1999.

［23］MAHMOUD H N，CONNOR R J，BOWMAN C A.Results of the fatigue evaluation and field monitoring of the I-39 Northbound Bridge over the Wisconsin River［R］.ATLSS report no.05-04.Bethlehem:Lehigh University，2005.

［24］STRAUSS A，FRANGOPOL D M，KIM S.Use of monitoring extreme data for the performance prediction of structures:Bayesian updating ［J］. Engineering Structures，2008，30:3654-3666.

Reliability prediction of bridge structures based on BDNM

FAN Xueping，LÜ Dagang
(School of Civil Engineering，Harbin Institute of Technology，150090 Harbin，China)

To predict the bridge structural reliability based on the monitoring information and the priori model of stress parameters(mean)，the dynamic measure of structural stress over time is treated as a time series，and considering the limitation of the BDLM，a Bayesian dynamic nonlinear model(BDNM)is then introduced.State equation and monitoring equation of monitoring stress are established with BDNM.Then the BDNM is approximately transferred into Bayesian dynamic linear model(BDLM)by Taylor series expansion technique，and the monitoring information is monitored by bayes factor.Combining parameters’ prior information with the early stress data containing noise，the stress state parameters are deduced with Bayesian Posterior Probability.A dynamic model is built to forecast the changing trend of structural stress.To allow for the epistemic uncertainty in variance estimation based on monitoring information，a discount factor approach is made for specification of unknown variance.Finally based on the built BDNM and the FOSM method，the structural reliability is predicted，and the feasibility and application of the built model is illustrated by an actual example.

bridge structural health monitoring;stress;BDNM;BDLM;reliability prediction

TU391;TU392.5

A

0367-6234(2014)02-0001-05

2013-03-04.

国家自然科学基金资助项目(50678057).

樊学平(1985—)，男，博士研究生;

吕大刚(1970—)，男，教授，博士生导师.

吕大刚，ludagang@hit.edu.cn.

(编辑 赵丽莹)