非极大弧连通有向图弧连通度的下界

王晓丽，王世英

（1．晋中学院数学学院，山西 榆次 030600；2．山西大学数学科学学院，山西 太原 030006）

非极大弧连通有向图弧连通度的下界

王晓丽1，王世英2

（1．晋中学院数学学院，山西 榆次 030600；2．山西大学数学科学学院，山西 太原 030006）

设D是一个有向图，δ（D）是最小度，弧连通度为λ（D），则λ（D）≤δ（D）。当λ（D）＜δ（D）时，称有向图D是非极大弧连通的。本文给出了非极大弧连通图的弧连通度的下界。

有向图；弧连通度；度序列；团数

1 引言

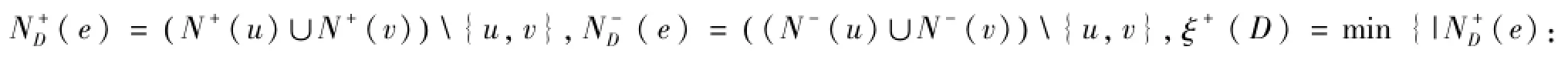
如果D的任意两个不同的顶点u，v，在D中都存在（u，v）－路，则称D为强连通的。对于强连通有向图D，若存在一个弧集SA（D），使得D-S不是强连通的，则称S是D的一个弧割。弧数最少的弧割称为最小弧割。D的弧连通度λ（D）定义为D的最小弧割中弧的数目。由定义显然λ（D）≤δ（D）。当λ（D）＜δ（D）时，称有向图D是非极大弧连通的。设D是一个有向图，令D1，D2，…，Dt是D的所有强连通分支排成的一个序列，若对任意的uv∈A（D），其中u∈A（Di），v∈A（Dj）都满足i＜j，则称上述的序列是D的一个强连通分支无圈序。

对整数p≥2，去掉有向图D中弧的方向，再去掉产生的重边得到的简单图若不含p＋1阶的完全子图，称D的团数ω（D）≤p。若X是V（D）的非空真子集，记＝V＼X。对有二分类V′，V″的二部有向图D及ZV（D），令Z′＝Z∩V′，Z″＝Z∩V″，本文未给出的术语和记号请参见文［1］。

文献［2］讨论了有向图点连通度的下界，本文讨论非极大弧连通图的弧连通度的下界。

2 主要结论

引理1［3］设（X，Y）为有向图D的任一满足｜（X，Y）｜≤δ－1的弧割，则｜X｜≥δ＋＋1，｜Y｜≥δ－＋1，且｜X｜≥ξ＋＋2，｜Y｜≥ξ－＋2。

证明设S是D的最小弧割，则｜S｜＝λ且D-S至少包含两个强连通分支。设D1，D2，…，Dk（k≥2）是D-S的强连通分支无圈序。令X＝V（Dk），Y＝V（D）＼V（Dk），由强连通分支无圈序的定义知，D-S中（X，Y）＝Ø。注意到D是强连通的，所以在D中（X，Y）≠Ø。从而（X，Y）S。又因为（X，Y）是D的一个弧割且S是最小弧割，故（X，Y）＝S。因为λ＜δ，所以由引理1知｜X｜≥δ＋＋1，｜Y｜≥δ－＋1，同时｜X｜≥ξ＋＋2，｜Y｜≥ξ－＋2，即｜X｜，｜Y｜≥max｛δ＋1，ξ＋2｝＝t。

将X中的点按度的不增序排列，由前t个顶点组成的集合记为U。将Y中的点按度的不增序排列，由前t个顶点组成的集合记为W。则我们有

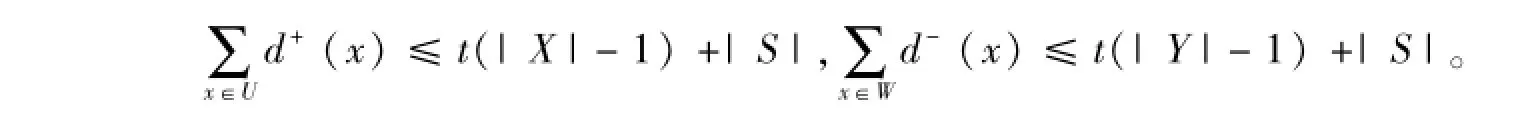
故

证明设S是D的最小弧割，则｜S｜＝λ且D-S至少包含两个强连通分支。设D1，D2，…，Dk（k≥2）是D-S的强连通分支无圈序。令X＝V（D1），Y＝V（Dk），由强连通分支无圈序的定义知，D-S中（Y，¯Y）＝Ø，，X）＝Ø，且｜X｜，｜Y｜≥2。若｜X｜＝1，设X＝｛x｝，则δ≤δ－≤d－（x）≤｜S｜＝λ，与λ＜δ矛盾，故｜X｜≥2。同理可证｜Y｜≥2。由于｜X｜，｜Y｜≥2，且D1，Dk是强连通的，故这两个分支D1，Dk都至少包含两条弧，设u1v1∈A（D1），u2v2∈A（Dk）。则我们有

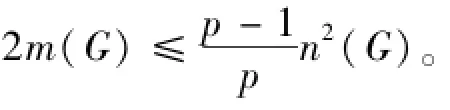
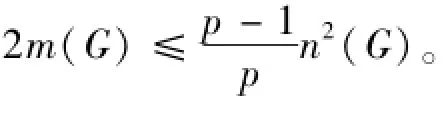
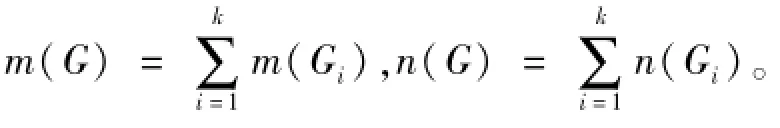
故结论成立。

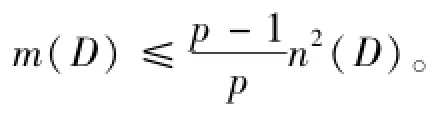
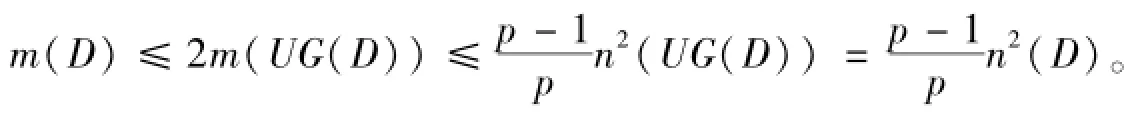
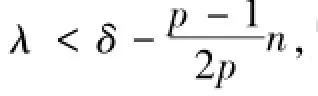
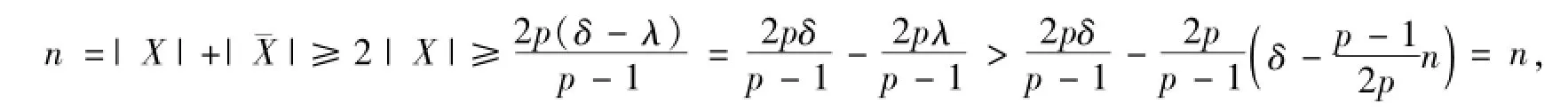
矛盾，故结论成立。

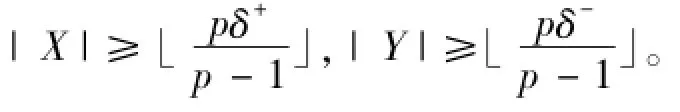
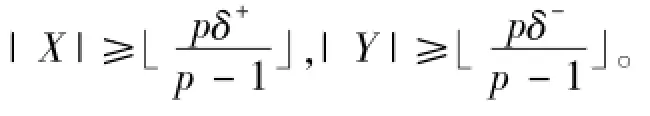
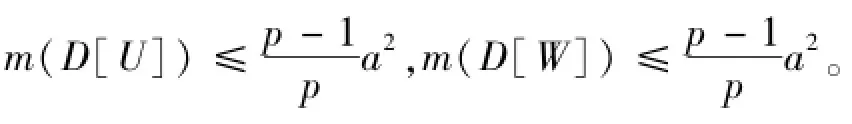
则我们有

引理6［3］设（X，Y）是二部有向图D的任一满足｜（X，Y）｜≤δ－1的弧割，则｜X′｜，｜X″｜≥δ＋，｜Y′｜，｜Y″｜≥δ－。

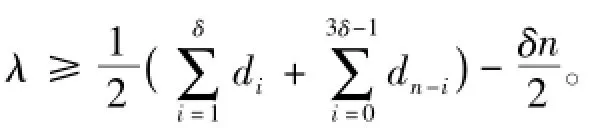
证明设S是D的最小弧割，则｜S｜＝λ且D-S至少包含两个强连通分支。设D1，D2，…，Dk（k≥2）是D-S的强连通分支无圈序。令X＝V（Dk），Y＝V（D）＼V（Dk），则（X，Y）＝S。因为λ＜δ，所以由引理6，知｜X′｜，｜X″｜≥δ＋，｜Y′｜，｜Y″｜≥δ－。即｜X′｜，｜X″｜≥δ，｜Y′｜，｜Y″｜≥δ。

将X′中的点按度的不增序排列，由前δ个顶点组成的集合记为U′。将X″中的点按度的不增序排列，由前δ个顶点组成的集合记为U″。将Y′中的点按度的不增序排列，由前δ个顶点组成的集合记为W′。将Y″中的点按度的不增序排列，由前δ个顶点组成的集合记为W″。则我们有

由此可得

［1］BANG-JENSENJ，GREGORYG．Digraphs：theory，algorithmsandapplications［M］．London：Springer-Verlag，2001．

［2］HELLWIGA，VOLKMANNL．Lowerboundsonthevertex-connectivityofdigraphsandgraphs［J］．InformationProcessing Letters，2006，99（2）：41－46．

［3］高敬振．有向图的边割（X，Y）中｜X｜和｜Y｜的下界与有向图的极大性和超级性［J］．系统科学与数学，2011，12（5）：1603－1611．

［4］TURÁNP．Anextremalproblemingraphtheory［J］．MatematikaiésFizikaiLapok，1941，48：436－452．

Lower bounds of the arc-connectivity of a non-maximally arc-connected digraph

WANG Xiao-Ii1，WANG Shi-ying2
（1．School of Mathematics，Jinzhong University，Jinzhong 030600，China；2．School of Mathematics，Shanxi University，Taiyuan 030006，China）

Let D be a digraph and δ（D）be its minimum degree．Then λ（D）≤δ（D）exists．A digraph D is non-maximally arc-connected if λ（D）＜δ（D）．This paper presents the lower bounds of the arc-connectivity of a non-maximally arcconnected digraph．

digraph；arc-connectivity；degree sequence；clique number

O157.5

A

1002-4026（2014）01-0098-04

10.3976／j.issn.1002－4026.2014.01.017

2013-04-01

国家自然科学基金（61070229）；国家教育部博士点基金（博导类）（20111401110005）

王晓丽（1982－），女，硕士，研究方向为图论。