数值优化改进的BP神经网络逼近性能对比研究

丁硕，常晓恒，巫庆辉，杨友林

（渤海大学工学院，辽宁 锦州 121013）

数值优化改进的BP神经网络逼近性能对比研究

丁硕，常晓恒，巫庆辉，杨友林

（渤海大学工学院，辽宁 锦州 121013）

为了比较不同的数值优化改进的BP神经网络的逼近性能，本文在MATLAB 7.0环境下，建立了三类基于数值优化改进的BP算法，并以非线性函数逼近为例，对7种典型的数值优化改进算法进行网络训练和仿真实验，得出了在不同环境下，每种数值优化差法逼近的可行性。

数值优化；BP神经网络；逼近性能；对比研究

数值逼近是指给定一组数据，用数学分析的方法来分析这组数据，常用的数学分析方法有多项式拟合和插值运算。由于人工神经元网络（Artificial Neural Networks，ANN）具有很强的非线性映射能力、自学习性和容错性，所以，近些年来采用ANN对非线性函数进行逼近成为该领域的一个研究热点，其优越性可在数据本身需要决定的模式特征不明确或含有噪声等情况下得到体现。目前，国内外学者绝大部分使用的ANN模型是BP神经网络，但是，传统的BP网络存在收敛速度慢、训练时间长和目标函数存在局部最小等缺点，所以，学者们提出了许多改进算法。BP网络算法，其实就是对于非线性函数进行优化。以往在求解此类问题时，经常利用数值优化的方法，因为该方法在求解非线性函数时具有收敛速度较快的优点，所以部分学者用其对BP算法进行改进。数值优化算法需要同时考虑非线性函数的一阶导数和二阶导数信息［1－3］。本文在详细分析了3类基于数值优化改进的BP算法的基础上，通过实例仿真，比较各类数值优化算法应用于BP神经网络后的逼近效果，得出在不同环境下，每种数值优化算法逼近的可行性。

1 数值优化改进的BP神经网络算法原理

1.1 共轭梯度优化算法原理

共轭梯度优化算法的实质是沿着梯度最陡的方向下降来对权值进行修正，误差函数沿着梯度最陡的方向下降最快，收敛速度比沿着梯度最陡的方向的收敛速度更快。典型的共轭梯度优化算法主要有4种，分别是：Fletcher-Reeves、Polak-Ribiere、Powell-Beale和Scaled Conjugate Gradient（SCG）优化算法。共轭梯度优化算法的首轮迭代过程为：

最佳线性搜索方向如式（2）所示：

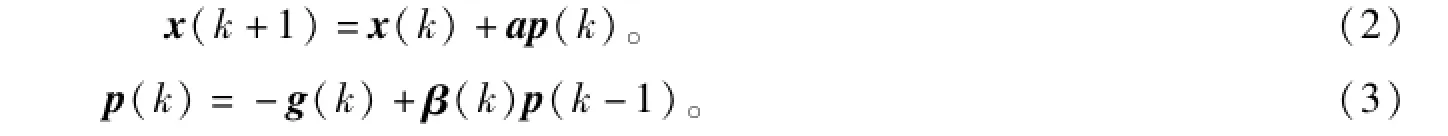
式（3）中，p（k）为经过k＋1轮迭代后的搜索方向，由前一轮迭代后的梯度、搜索方向共同决定，β（k）的算法视其具体属于哪一种共轭梯度优化算法而定。在MATLAB的Toolbox中，Fletcher-Reeves优化算法对应的训练函数为traincgf（β（k）的算法如式（4）所示），Polak-Ribiere优化算法的对应的训练函数为traincgp（β（k）的算法如式（5）所示）［4］。

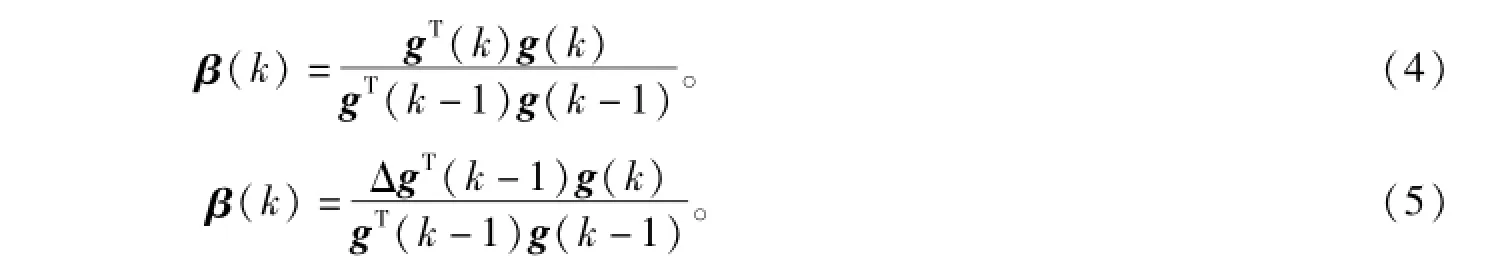
Powell-Beale优化算法的迭代过程为：

SCG优化算法在4种共轭梯度优化算法中迭代过程最为简单，计算量最小。

1.2 拟牛顿优化算法原理

拟牛顿法是一种改进BP算法的常见数值优化方法，其理论基础是牛顿法。拟牛顿算法的权值更新如式（8）所示：

式（9）中，方向向量p（k）用梯度向量g（k）来定义，矩阵S（k）是每次迭代中调整的正定矩阵，这样做的目的在于方向向量d（k）逼近牛顿法的方向｛H（k）｝－1×▽f（x（k））。令q（k）＝g（k＋1）－g（k），Δw（k）＝w（k＋1）－w（k），且通过逼近式（10）可以成立。

用S（k）去逼近H（k），则式（11）可以成立。

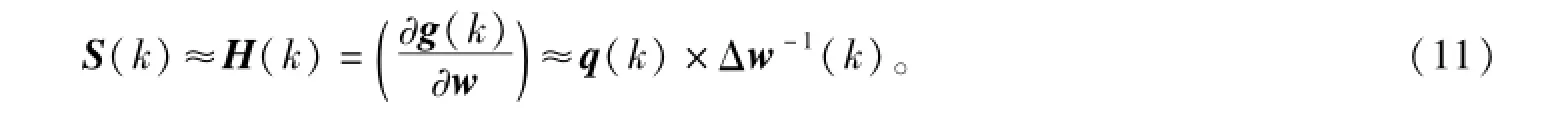
当误差函数是二次函数时，式（11）是精确的，拟牛顿算法实现了对Hessian矩阵H（k）的逼近。H（k）的近似矩阵S（k）根据式（11）使用递归公式可得：

当式（12）中ε（k）取值不同时，逼近Hessian矩阵的方法不同［5］。比较典型的是BFGS（Broyden，Fietcher，Goidfard，Shanno）优化算法和一步割线优化算法。在MATLAB的Toolbox中，采用BFGS优化算法和一步割线优化算法的训练函数分别为trainbfg和trainoss。

1.3 LM（Levenberg-Marguardt）优化算法原理

LM算法与拟牛顿算法一样是为了在近似二阶训练速率进行修正时避免计算Hessian矩阵而设计的。若误差函数用平方和表示时，可以用下式来表示Hessian矩阵：

梯度表达式如为：

式（13）中，J（k）是包含网络误差对权值和阈值的一阶导数的雅克比矩阵，式（14）中，e为误差向量。

LM算法可按照下式进行修正：

式（15）中，I为单位矩阵，比例系数μ是一个大于0的很小的参数，当μ接近0时，式（15）变为牛顿法；当μ很大时，式（15）变为梯度下降法。因为牛顿法在对最小误差进行逼近时，收敛速度快、精度高，所以应使式（15）最终接近于牛顿法，使μ减小；仅在进行尝试性迭代后的误差性能增加的情况下，才使μ增加［6－7］。在MATLAB的Toolbox中，LM算法对应的训练函数为trainlm。

2 数值优化改进的BP神经网络的建立

建立数值优化改进的BP神经网络，主要包含网络层数、隐层神经元个数、初始权值和学习率4个要素。

2.1 网络层数的确定

根据ANN的函数逼近理论，1个3层BP网络可以逼近任意非线性函数。网络层数越多误差越小，精度越高，但另一方面会增加网络的复杂性，使训练时间延长。一般来讲，在预设的精度范围内，具有单隐层的BP神经网络足以逼近非线性函数。因此，本文在进行函数逼近实验时，BP神经网络采用单隐层结构。

2.2 隐层神经元个数

隐层神经元数目的冗余将使网络庞大、训练困难，而不足又会导致训练失败。隐层神经元数目与输入、输出层神经元数目相关。本文采用动态法来确定隐层神经元数，即一开始选用较少的隐层神经元，如果学习一定次数后效果不好，再增加隐层神经元，一直达到比较合理的隐层神经元数为止。经过多次实验，隐层神经元数最终确定为13，可以达到逼近要求。

2.3 初始权值的选取

初始权值对于非线性的BP神经网络的收敛程度和训练时间影响很大。若初始权值过大，会造成输入值在加权后落入传递函数的饱和区，进而使得训练停止。所以，本文在建立数值优化BP神经网络时，输入值在加权处理后尽可能接近0，这样可以保证初始权值的调整发生在S型传递函数的斜率最陡处。

2.4 学习率

学习率过大，系统就会不稳定；相反，网络的训练时间就会延长，收敛速度缓慢，最终陷入局部最小值0，所以学习率一般选取（0.01，0.8）之间。本文为了兼顾系统稳定性和较快的收敛速度，学习率选取为0.1。

3 7种数值优化BP神经网络的逼近性能仿真对比

针对共轭梯度算法、拟牛顿法和LM算法分别设计实现了7种数值优化BP神经网络，由样本数据实现对如式（16）所示的非线性函数逼近。

MATLAB7.0作为计算机仿真平台，输入样本数据为x∈［0，8］，采样间隔是0.1，样本总数是80个。因为线性神经网络的学习规则是Widrow-Hoff学习规则，又称为最小均方误差（Least Mean Error，LMS）学习算法，所以本文在建立数值优化BP神经网络时所选用的误差准则为均方误差（MSE），其计算公式如式为：

式（17）中，k＝1，2，…，表示输入向量与对应的期望输出向量样本对的数量，dk＝（d1（k），d2（k），…），表示网络的期望输出向量，yk＝（y1（k），y2（k），…）表示网络的实际输出向量。选取Sigmoid作为激活函数，在MSE预置误差精度为0.000 01，学习率0.1，学习次数设为20 000次时，对共轭梯度算法、拟牛顿法和LM算法进行计算机编程，并对网络进行训练和仿真逼近，取20次计算机运算的平均值作为实验最终结果。7种优化算法对于目标函数的实际逼近结果如图1～7所示。7种数值优化改进BP算法仿真结果对比见表1。

表1 数值优化改进BP算法仿真结果对比Table 1 Simulation result comparison of numerical optimization improved BP neural network algorithms

图1 Fietcher-Powell算法逼近结果Fig.1 Approximation results of Fietcher-Powell algorithm

图2 Polak-Ribiere算法逼近结果Fig.2 Approximation results of Polak-Ribiere algorithm

图3 Powell-Beale算法逼近结果Fig.3 Approximation results of Powell-Beale algorithm

图4 SCG算法逼近结果Fig.4 Approximation results of SCG algorithm

图5 一步割线算法逼近结果Fig.5 Approximationresultsofone-step secantalgorithm

图6 BFGS算法逼近结果Fig.6 ApproximationresultsofBFGS algorithm

由图1～3可以看出，在4种典型的共轭梯度算法中，Fletcher-Reeves算法、Polak-Ribiere算法和Powell-Beale算法的逼近效果很差，在目标函数斜率变化较大处均出现了很大程度的逼近误差，且在规定的最大收敛步数范围内，最终未能完成逼近任务，均方误差也未能达到逼近要求，且误差很大。

图7 LM算法逼近结果Fig.7 ApproximationresultsofLMalgorithm

由图4和表1可以看出，在4种典型的共轭梯度算法的逼近性能中，采用SCG算法训练较其他共轭梯度算法需要的迭代次数显著减少，收敛速度较快，均方误差明显较其他3种典型的共轭梯度算法减小，达到了逼近误差要求，完成了逼近任务，这是因为SCG算法不用进行行搜索。由图5～6可以看出，BFGS和一步割线算法的整体逼近效果优于4种典型的共轭梯度算法。由表1可以看出，在2种典型的拟牛顿算法中，BFGS算法的收敛步数较一步割线算法少，逼近精度也明显优于一步割线算法，但因为要存储近似Hessian矩阵，BFGS算法每步迭代的计算量和内存需求大于共轭梯度法。总的来说，在训练稍小网络时使用BFGS算法效果较好，拟牛顿法的逼近性能优于共轭梯度法。LM算法收敛速度最快，且精度也最高，逼近结果远远小于其他数值优化算法的均方误差，具有最佳的逼近性能见图7。

4 结语

由于无法对所有非线性函数一一进行逼近，本文仅以一个函数为例设计了实验。对于不同函数进行逼近实验，BP神经网络的学习时间有很大差别，但各类优化算法误差收敛快慢的优劣趋势没有很大变化。可以看得出共轭梯度法的逼近效果相对较差。一般来讲，共轭梯度算法要求在每次迭代时进行行搜索，而这种行搜索导致收敛速度明显慢于LM算法和拟牛顿算法。在4种典型的共轭梯度算法中，SCG算法和其他3种共轭梯度算法相比，需要较少的迭代次数，勉强达到逼近精度要求。采用LM算法收敛速度最快，如果就训练准确性和逼近精度来讲，该算法明显优于其他几种数值优化算法，但该算法需要计算误差函数的二阶导数，算法的复杂度增大，因此，当BP神经网络的结构相对简单且网络参数很少时，该算法比较容易实现，仿真效果好；当BP神经网络的结构比较复杂时，该算法在计算过程中会产生大量的中间结果矩阵，需要较大的计算机内存空间，实现LM算法的难度会大大增加。所以在中小型网络中应优先采用LM算法进行逼近。尽管拟牛顿算法进行逼近时要求存储近似Hessian矩阵，但仍比共轭梯度法的收敛速度要快，仅次于LM算法。所以，如果内存空间较小，也可以尝试使用拟牛顿算法。

［1］高雪鹏，丛爽．BP网络改进算法的性能对比研究［J］．控制与决策，2001，16（2）：167－171．

［2］周黄斌，周永华，朱丽娟．基于MATLAB的改进BP神经网络的实现与比较［J］．计算技术与自动化，2008，27（1）：28－31．

［3］曹旭帆，叶舟，万俊，等．基于BP神经网络的函数逼近实验及MATLAB实现［J］．实验室研究与探索，2008，27（5）：34－38．

［4］丁硕，巫庆辉．基于改进BP神经网络的函数逼近性能对比研究［J］．计算机与现代化，2012（11）：10－13．

［5］刘天舒．BP神经网络的改进研究及应用［D］．哈尔滨：东北林业大学，2011．

［6］DING S，WU Q H．A MATLAB-based study on approximation performances of improved algorithms of typical BP neural networks［J］．Applied Mechanics and Materials，2013，313／314：1353－1356．

［7］智会强，牛坤，田亮，等．BP网络和RBF网络在函数逼近领域内的比较研究［J］．科技通报，2005，21（2）：193－197．

Comparative study of approximation performance of numerical optimization improved BP neural networks

DING Shuo，CHANG Xiao-heng，WU Qing-hu i，YANG You-Iin
（School of Industry，Bohai University，Jinzhou 121013，China）

We address numerical optimization improved BP neural network algorithms to compare their approximation capabilities. We establish three kinds of numerical optimization improved BP algorithms in MATLAB 7.0. Network training and simulation test are then performed for seven typical numerical optimization improved algorithms with non-linear function approximation as an example. We compare the approximation performance of different numerical optimization in defferent environments.

numerical optimization；BP neural networks；approximation performance；comparative study

TP391.9

A

1002-4026（2014）01-0068-05

10.3976／j.issn.1002－4026.2014.01.012

2013-07-02

国家自然科学基金（61104071）；辽宁省教育厅科学研究一般项目（L2012402）

丁硕（1979－），男，讲师，研究方向为动态检测、测试信号处理以及虚拟仪器。Email：dingshuo2004＠sina．com