有限域随机变量限界概率分布函数模型

邹毅，王君杰

（1．中国人民大学信息学院，北京 100872；2．同济大学桥梁工程系，上海 200092）

有限域随机变量限界概率分布函数模型

邹毅1，王君杰2

（1．中国人民大学信息学院，北京 100872；2．同济大学桥梁工程系，上海 200092）

针对随机变量正态分布函数等的理想化情况，提出了限界修正的方法，并给出了线性函数修正和二次函数修正两种具体的修正结果。以美国AASHTO桥梁船撞设计指南中船舶碰撞概率的计算方法为例，说明了限界修正在工程领域中的重要性。

随机变量；概率密度函数；有限域

在科学与工程领域，当对物理现象进行定量数学建模时，一些物理量表现出很强的不确定性，其中绝大多数可以描述为随机性，具有随机性的物理量称为随机变量。恰当的描述随机变量可以确定其概率分布函数，这样就可以得到该随机变量的完整的统计描述。从目前的研究与应用的情况来看，广泛使用的随机变量的概率描述数学模型主要有正态分布、对数正态分布、极值分布等［1－2］。这些应用广泛的分布函数的数学模型一般都定义在（－∞，＋∞）或（0，＋∞）上。但任何现实的物理量都不可能取值－∞或＋∞，数学模型的这种处理是对真实物理现象的理想化处理。这种理想化处理在很多情况下可以给出合理地分析和预测结果，但对于一些工程问题，这种理想化则不能合理的分析和预测结果，需要进行必要的限界修正。本文针对应用最为广泛的正态分布模型进行限界修正，并以案例说明这种修正的实际意义。

1 修正模型的一般表达形式

假定X是可以理想化为正态分布的随机变量，其概率密度函数为f（x），定义在（－∞，＋∞）区间上。对于实际的工程问题，随机变量X的取值区间是有限的，记为（x1，x2），其中x1和x2取有限值。考虑到随机变量X的取值区间为有界的实际情况，进行如下修正，得到概率分布函数模型

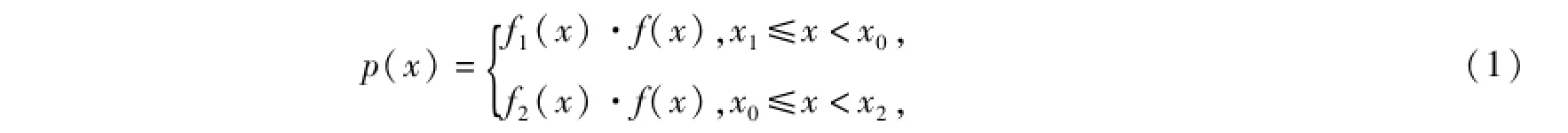
其中x0为f（x）取最大值处，f1（x）和f2（x）称为修正函数，p（x）称为修正的限界概率密度函数。

记p（x）在x＝x0处得最的大值为pmax，则有

记p（x）在x＝x1处取值为p1，在x＝x2处取值为p2，则有

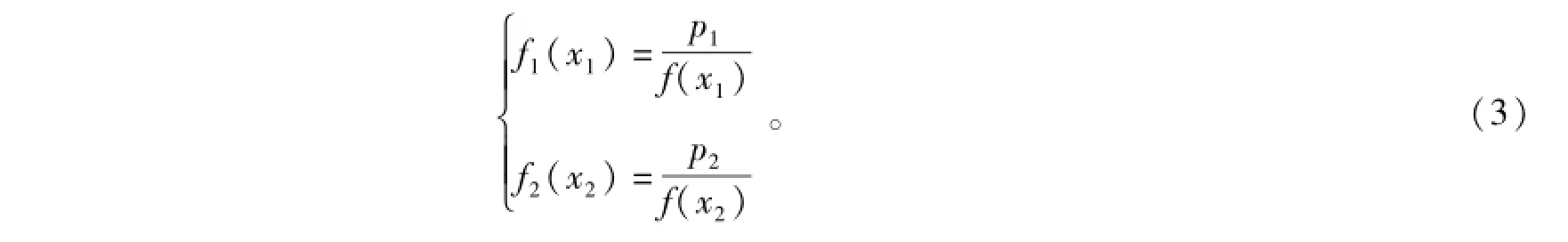
理论上讲，f1（x）和f2（x）可以取任何合理的函数，但出于简单考虑，这里选取线性函数和二次抛物线函数。

2 线性修正函数

最简单的修正函数可以选线性函数。利用f1（x）和f2（x）在x0、x1和x2处的函数取值（式（2）和（3）），可以得到

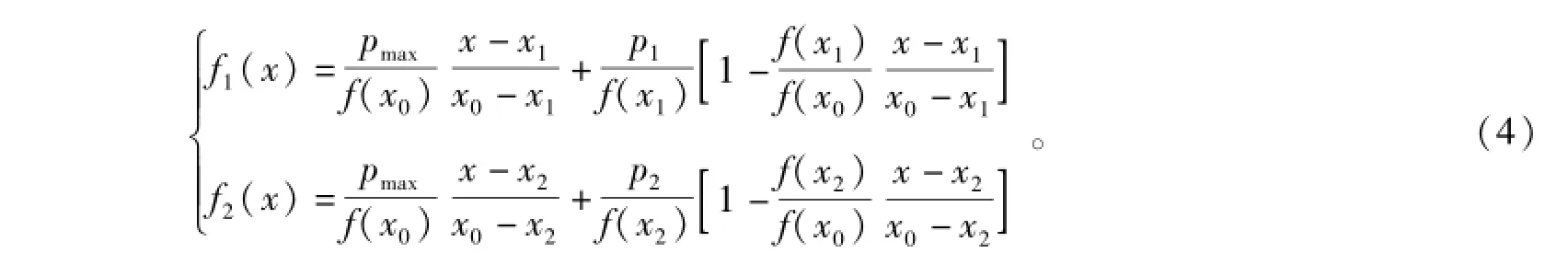
修正过的概率密度函数p（x）必须满足

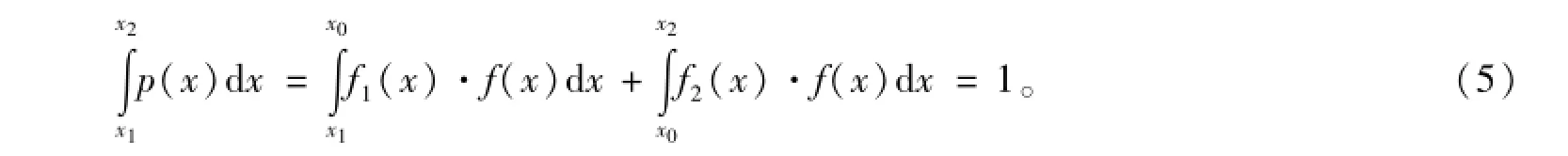
据此，对于线性函数，可以得到

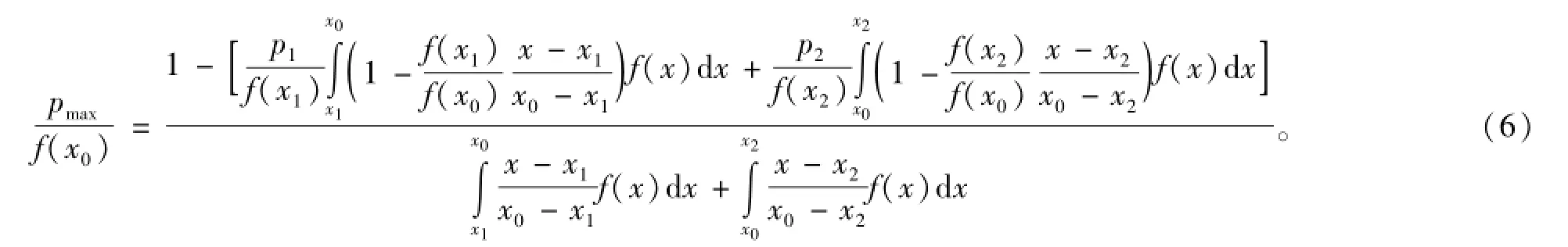
采用线性修正函数得到的修正结果见图1。

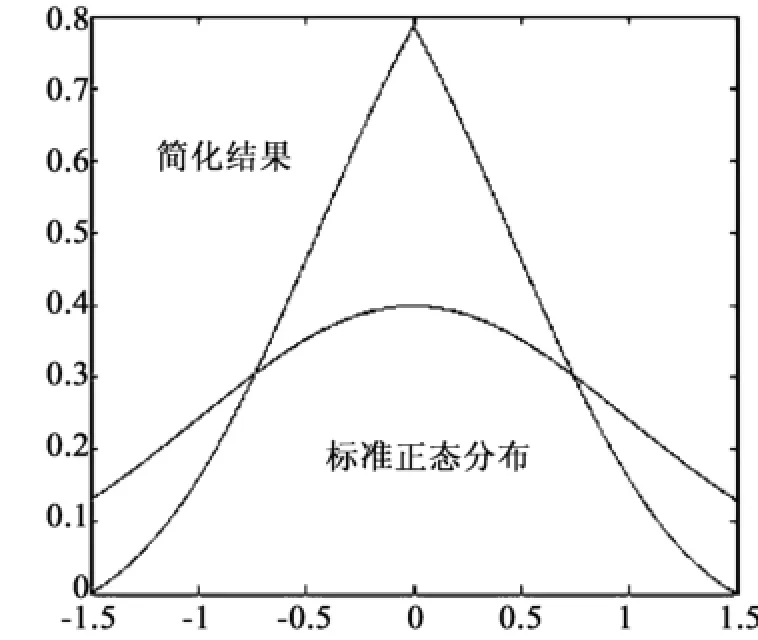
图1 线性修正结果Fig.1 linear correction results

3 二次抛物线修正函数

对于二次抛物线函数，除了利用f1（x）和f2（x）在x0、x1和x2处的函数取值（式（2）和（3））外，还需要补充条件：在x＝x0时，f1（x）取极值f′1（x0）＝f′2（x0）＝0。即，据此可以得到

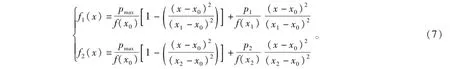
对于二次函数，根据式（5），可以得到

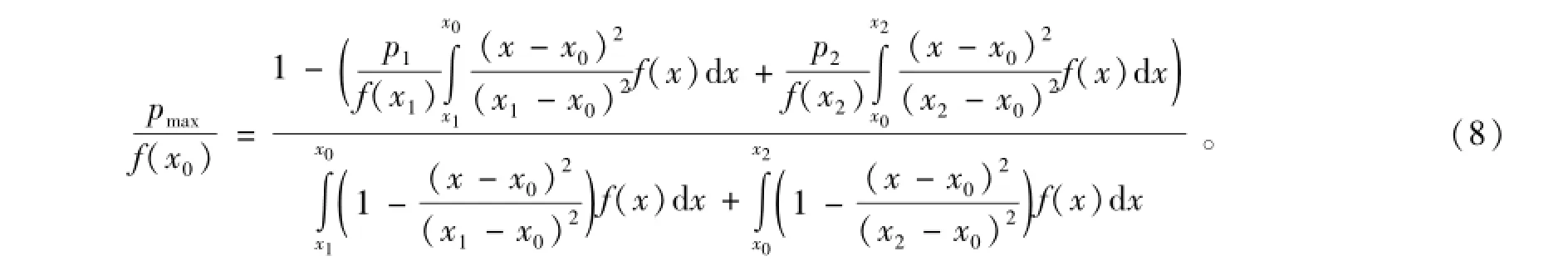
采用线性修正函数得到的修正结果见图2。

对正态概率密度函数的修正，目的是考虑自变量域的有界性，这一点对有些工程实际问题是重要而不能忽略的。修正的一个基本考虑是经过修正的概率密度函数，与域内原正态概率密度函数的性质接近，如光滑性、凹凸变化等。经二次抛物线修正后的概率密度函数在性质上与原正态概率密度函数更接近，因此与线性函数修正相比，这是更好的修正方案。

4 应用

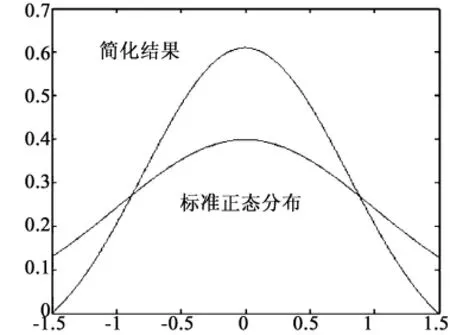
图2 二次抛物线修正结果Fig.2 Correction result of quadratic parabola

目前，国内外船舶与近海工程结构碰撞概率的计算［3－9］，其几何分布均定义为正态分布。但河道与航道都是有界的，因此理想化的正态分布与实际情况有差别。本文以这一工程应用为背景，来说明限界修正的必要性。计算对象为一座跨越航道的大桥，平面布置为4×50 m＋2×160 m＋13×50 m，如图3所示，桥墩编号从16号到35号［10］。

为了表达定量反映限界修正的影响，定义如下比值

式中，pm为限界修正后的碰撞概率，p为无修正时的碰撞概率。

图4是比值ρ的计算结果。由图4可见，进行限界修正后，对于远离航道的桥墩船撞频率会减小，而且离航道越远减小的程度越大；对于靠近航道处的桥墩，进行限界修正后撞击频率可能会变小也可能会变大（如下行船舶撞击23号墩的频率在进行限界修正后会变大）。原因是随着偏离分布曲线中心点距离的增加，修正概率密度函数和未修正概率密度函数的函数值偏差会呈递增趋势。图4显示，考虑河道与航道的有界性后，船舶航迹采用二次函数修正的限界正态概率分布函数，对船舶碰撞频率的估计结果的影响显著，离航道中心线越远影响越大（减小）。该例表明，正态分布函数的限界修正具有实际工程意义。

图3 九江大桥桥跨布置Fig.3 Layoutof Jiujiang bridge and its navigational channels

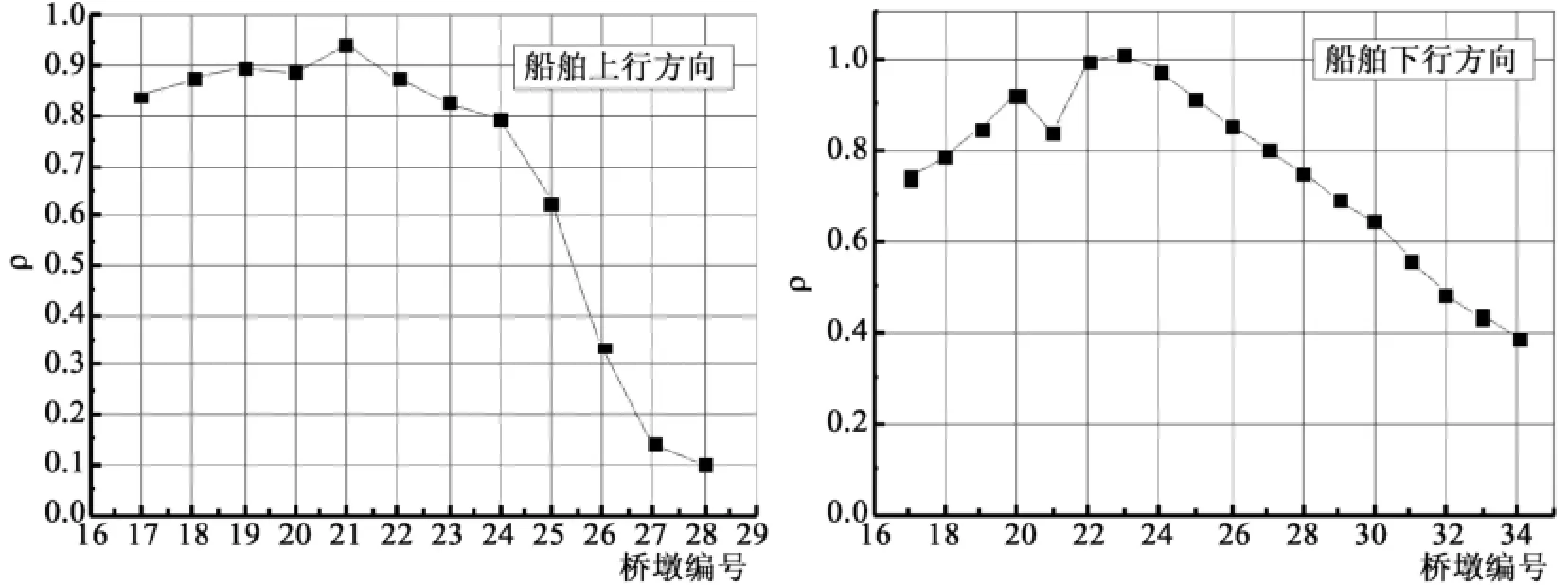
图4 限界修正对船舶撞击频率的影响Fig.4 Impactof limited domain correction on vessel collision frequency

［1］贡金鑫．工程结构可靠度计算方法［M］．大连：大连理工大学出版社，2003．

［2］高谦，吴顺川，万林海，等．土木工程可靠性理论及其应用［M］．北京：中国建材工业出版社，2007．

［3］AASHTO．Guide specification and commentary for ship collision design of highway bridges［M］．Washington，D．C：American Association of State Highway and Transportation Officials，2009．

［4］EN 1991-1-7．General Actions-Accidental Actions due to Impact and Explosions［S］．

［5］KUNZCU．Ship Bridge Collision in River Traffic，Analysis and Design Practice［M］．London：Aa Balkema Rotterdam，1998：13－21．

［6］KARLSSON M，RASMUSSEN F M，FRISK L．Verification of ship collision frequency model［M］．London：AA Balkema Rotterdam，1998：117－121．

［7］戴彤宇，刘伟力，聂武．船撞桥概率分析与预报［J］．哈尔滨工程大学学报，2003，24（1）：23－25，29．

［8］JCSS．Probabilistic Model Code［EB／OL］．［2013－09－10］．http：／／www．jcss．byg．dtu．dk／～／media／Subsites／jcss／english／publications／probabilistic_model_code／impact．ashx．

［9］ZHANG SW．Studies on the Probabilistic Model for Ship-Bridge Collisions［J］．International Journal of Statistics and Frequency，2013，2（1）：16－23．

［10］潘放，王君杰，李卫民，等．九江大桥船撞风险评估与防撞系统方案研究技术报告［R］．上海：同济大学，2010．

Modified probabilistic density function of a random variable in a limited domain

ZOU Yi1，WANG Jun-jie2
（1．School of Information，Renmin University of China，Beijing 100872，China；2．Department of Bridge Engineering，Tongji University，Shanghai 200092，China）

We presented a limited domain modification approach for the ideal condition of normal distribution of a random variable．We also proposed two concrete modification results of linear function and quadratic function modification．We further demonstrated the importance of limited domain modification of probabilistic density function in science and engineering，taking the computational method of vessel-bridge collision probability in USA AASHTO guide for bridge-vessel collision design as an example．

random variable；probabilistic density function；limited domain

TB115

A

1002-4026（2014）01-0106-04

10.3976／j.issn.1002－4026.2014.01.019

2013-10-10

交通运输部西部科技项目（200731882234）；交通部行业联合科技攻关项目（2008-353-344-340）

邹毅（1992－），男，学士，研究方向为应用数学。Email：zouyiapply＠sina．com