球形陆基充气天线反射面初始形态的确定

唐渝思，蒋金华，b，陈南梁，b

（东华大学a.纺织学院；b.产业用纺织品教育部工程研究中心，上海 201620）

球形陆基充气天线反射面初始形态的确定

唐渝思a，蒋金华a，b，陈南梁a，b

（东华大学a.纺织学院；b.产业用纺织品教育部工程研究中心，上海 201620）

利用有限元软件ANSYS及其参数化语言APDL建立了球形陆基充气天线反射面模型.结合抛物面的边界及受力特点对模型进行了逆迭代分析，得到了天线反射面的初始形态.分析结果表明，逆迭代法效率较高，经过少量迭代次数便可得到精度较高的初始形面.

充气天线；逆迭代；平衡态；初始形态

传统的便携式小型天线大部分是刚性结构，其质量偏重，不方便折叠携带，具有可移动性差、操作复杂且耗时、精度受拼装效果影响大等缺点，而使用球形充气天线可有效解决上述问题［1］.球形陆基充气天线采用薄膜或纺织材料制成，质量很轻，天线外有球形充气外罩保护，因而雨雪天气和风载荷对天线反射面的影响大大减弱，且具有很强的移动性和应急性［2-3］.球形陆基充气天线采用一种新型的结构形式，与传统的固面天线相比，其具有质量轻、折叠率高、运输方便、展开快速、高增益、低噪声辐射、高带宽等优点，是制作大口径天线的首要选择［4］.

国外对陆基充气天线的研究较多，美国GATR技术公司研制的充气天线系统已成功地配置在各种防御作战部队中，用于恶劣天气、紧急状况以及战争情况［5］.目前，该公司产品的使用范围已覆盖美国、非洲、伊拉克和阿富汗等国家和地区［5］.国内对陆基充气天线的研究起步很晚，且大多集中在天线反射面形面精度的测量以及用软件模拟分析等.其中，文献［1，4］制作了陆地用球形充气可展开天线的样机，利用数值方法对抛物面进行了保形设计，建立有限元模型分析了各参数对形面精度的影响.文献［6］通过对国内外充气式可展开天线研究成果的分析，设计了用于地面接收、发射卫星信号的球形充气式可展开反射面天线，并对天线馈源系统的基础理论进行了探讨.

球形陆基天线反射面初始形态的确定是天线系统制作的首要环节，国内外对充气天线反射面初始形态的研究主要集中在空间充气天线，其天线的结构形式及约束条件与球形陆基充气天线存在很大差异.本文在总结国内外对充气天线反射面初始形态的确定方法的基础上，选择非线性有限元法，采用逆迭代的方式，得到了精度较高的反射面初始形态，可参照初始形态进行放样加工，为自主生产制造此类天线提供依据.

1 天线的结构及成形方式

球形陆基充气天线系统包括一个由聚氯乙烯膜材制作的可充气中空球形外罩和置于其内部的抛物面反射面天线.反射面以镀金属的机织物制成，其边缘固定于中空球体的内壁上，将球体隔成上下两个相互独立的密闭半球体.上、下半球体各设充气口，在使用时，通过上、下半球的气压差来控制抛物面天线的形状.本文中充气展开球形天线设计半径r为900 mm，焦距为1 087.2 mm，焦径比为0.604，设计气压为100 Pa，天线结构简图如图1所示.天线系统的反射面设计为旋转抛物面，旋转抛物面由抛物线绕轴旋转而成.

图1 球形天线结构Fig.1 Structure of the spherical antenna

天线作为一种电气元件，其电性能是实际运用中重要的性能指标，天线反射面精度是反映天线结构和电性能的重要参数.如果反射面精度不高，即反射面偏离设计抛物面过多，使用过程中，在反射器中心聚焦的能量将会产生巨大的损失，这会导致天线的增益降低，从而影响天线的正常工作.而天线反射面精度与结构设计参数、加工制作工艺、成形方式有很大的关系.

目前，抛物面的成形方式主要有3种［7］：（1）初始平面形状的平面膜片在气压下变形为近似抛物面形状；（2）薄膜制作过程中采用模具直接加工成曲面薄膜；（3）若干平面膜片拼接形成曲面形状.结合抛物面的3种成形方式和制作加工的可行性，球形陆基充气天线反射面采用拼接曲面成形.如图2所示为反射面初始状态在气压作用下变形为设计状态.初始形面即由若干平面膜片拼接形成曲面，该形面经过一定的载荷施加后变形到理想设计状态的形面.

图2 抛物面反射面成形Fig.2 Parabolic reflector forming

2 反射面初始形态的确定

2.1 初始形态确定的必要性

初始形态的确定是薄膜结构设计中至关重要的一步，也是设计中的一个难点［8］.球形陆基充气天线的边界条件和初始预应力与一般的柔性张拉薄膜结构有所不同，在制作和使用过程中，其状态可以分为下述两个阶段.

（1）放样态：抛物面反射面与外部支撑体系安装完毕，未进行充气施加预应力的状态；

（2）理想平衡态：抛物面反射面在自重和预应力作用下的平衡状态.

制作过程中将若干平面材料拼接成放样态曲面，放样态曲面经变形得到实际使用时的理想平衡态形面.对于一个既定抛物面反射面天线，从设计图纸上能够确定理想平衡态几何参数（抛物面天线工作时的几何参数）和充气压的设计值.反射面在设计压力下可能发生较大的变形，即理想平衡态和放样态下的几何形态可能存在较大差异，结构能否按照设计图纸进行下料、放样与安装有待研究.合理的做法是先对反射面进行形态分析，确定放样态下结构的几何形状，并以此为分析起点，进行结构受力的模拟及后续分析计算.由此，天线反射面的初始形态的确定显得尤为重要.

2.2 初始形态确定的方法

对于柔性薄膜结构，常用初始形态确定的方法有 力 密 度 法［9-10］、动 力 松 弛 法［11］、非 线 性 有 限 元法［8］、能量法［12］等.充气膜结构反射面在充气压力和一定边界条件的作用下薄膜的应力分布不均匀，无法运用等张力假定的力密度法、动力松弛法等通用膜结构找形方法［13］.因此，本文采用非线性有限元法进行分析，在分析过程中，不采用等应力假定，直接采用材料真实的弹性模量和泊松比.

2.3 逆迭代法确定初始形态

对放样态形态｛X｝0施加一定作用力F，达到理想平衡态｛X｝.｛X｝为已知向量，欲求未知向量｛X｝0，就是求解非线性方程组的过程，逆迭代法则是求解非线性方程组的常用方法［14］.

采用逆迭代法来确定抛物面初始形态，其基本思想是应用真实的材料参数、荷载及边界约束条件，并以理想平衡态构形建立模型，通过非线性分析来求解.逆迭代流程如图3所示，即采用理想平衡态的抛物面尺寸建立有限元模型，然后对其施加压力进行非线性计算，得到近似理想平衡态和相应的位移，再将此平衡态的几何尺寸与设计图中真正的理想平衡态的几何尺寸的差值反向增加到原有模型的节点坐标上，作为设计放样态重新建模，并对新建的模型进行非线性分析，将分析得到的平衡态与理想平衡态进行比较.如果坐标误差足够小，即可视此次所得平衡态满足要求，而与之对应的设计放样态为近似放样态.如果差值不满足精度要求，则将此差值作为回缩量再次反向增加到前一次放样态模型上，并再次进行分析，直到满足精度要求.

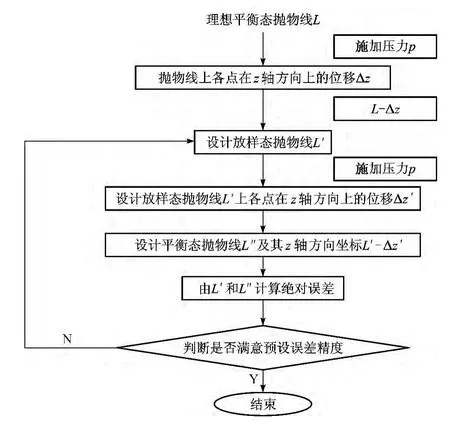
图3 逆迭代流程Fig.3 Inverse iteration process

尽管上述逆迭代的思路比较清晰，但具体实现过程存在一定难度，主要来自非线性程序的编制和调试.在抛物面初始形态确定的过程中，需要对模型进行多次修改，分析时存在很多过程的重复和判断.采用ANSYS软件进行结构分析的同时，利用其APDL语言编制后处理程序，对其中重要的数据进行编辑和处理，可以较方便地求得抛物面的初始形态.

3 抛物面模型的建立与分析

3.1 抛物面模型的建立及分析流程

由于旋转抛物面可由其母线经过旋转得到，为此只需研究其母线的初始位置.结合本抛物面的设计参数，充气后反射面方程可表示为

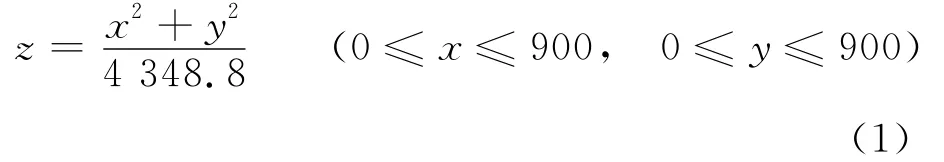
抛物面的母线及其方程如图4所示.

图4 抛物面反射面母线Fig.4 Bus of the parabolic reflector

具体分析流程如下：（1）建立结构的有限元模型；（2）定义材料参数、模型边界条件及设计气压值；（3）获取在母线上的有限元节点并定义节点理想平衡态的坐标数组为W1、节点设计放样态坐标数组为W0、节点设计平衡态坐标数组为W2、节点设计平衡态与理想平衡态的差值数组为W；（4）提取模型节点坐标并赋值给数组W1x和W1z；（5）进入求解器，进行第一次非线性求解；（6）进入后处理，验证迭代结果是否满足求解精度；（7）若不满足精度要求，更新节点坐标；（8）进入求解器，再次非线性求解.

在对模型非线性求解时，应指定分析类型为静力分析并打开大变形效应，结合充气过程实际情况，选择载荷为线性增加方式.对于非线性方程组的求解技巧，通常选择完全N-R法进行，利用张力补偿法进行迭代求解.为保证分析的顺利完成，需适当地设定最大循环次数.在验证迭代结果是否满足求解精度时，采用坐标差值Δz的均方根（RMS）作为判断依据，其计算式为

其中：Δzi为节点i设计平衡态与理想平衡态坐标差值.

3.2 结果分析

由于对称性，采用母线旋转30°所形成的结构作为分析模型.分析时采用材料真实的弹性模量和泊松比，反射面材料由锦纶镀银纱线织造的机织物贴合一层可保证气密性的膜组成.弹性模量和泊松比采用双轴比例加载法测得，试验方法参照文献［15］.

结构有限元模型网格如图5所示，对其分析时圆周采用固定边界，两条母线采用对称约束.结构采用的单元类型为shell 41，单元总数为864，预设精度为0.15 mm，压力载荷为两半球气压差100 Pa.对模型第一次施加压力后，在边界条件下，运用几何非线性求解，经计算后得到的膜面的位移云图如图6所示.从图6可以看出，当抛物面圆周边界固定时，在受到均布气压载荷时，膜面的轴向位移沿径向逐渐减小，膜面中心处的轴向位移最大.

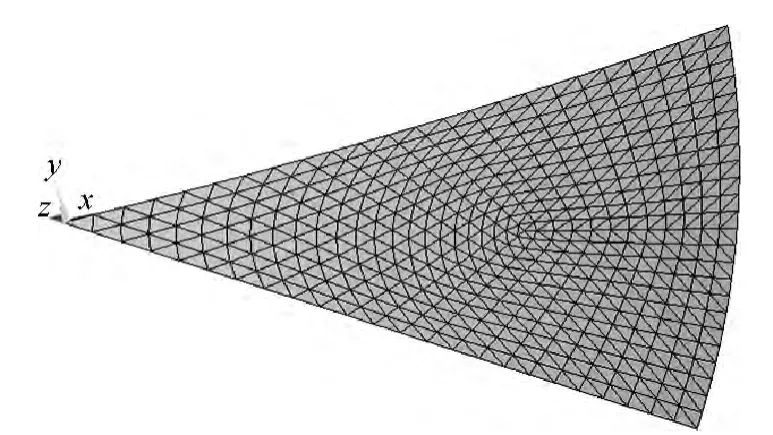
图5 模型网格图Fig.5 Mesh of the model

图6 第1次迭代轴向位移云图Fig.6 Displacement of axes direction after the first iteration

按照前述流程对模型进行分析，表1为迭代次数与形面坐标偏差Wmax（设计平衡态与理想平衡态坐标差值数组最大值）的关系.从表1可以看出，随着迭代次数的增加，Wmax逐渐减小，前3次所求得的Wmax较大，从第4次迭代开始，Wmax下降到1 mm以下，且随着迭代的进行偏差值下降的速度趋缓.

表1 迭代次数与形面坐标偏差的关系Table1 Relationship between iterations and surface coordinate deviation mm

图7 迭代结果Fig.7 Results of the iterations

如图7所示为逆迭代结果.从图7（a）可以看出，两形面坐标差值的RMS随着迭代次数的增加下降明显，从第4次迭代开始下降趋势变缓.第9次迭代结束后，RMS已下降到0.148 mm，此时已能满足精度的要求，第9次迭代得到的设计放样态可视为满意的形面初始态.从图7（b）迭代偏差分布可以看出，使用逆迭代对抛物面找形，第1次迭代结果得到的设计平衡态形面与理想平衡态形面坐标存在较大的偏差.将此偏差作为回缩量修正设计放样态模型后再次进行迭代，得到第2次设计平衡态形面与理想平衡态形面坐标的偏差明显小于第1次迭代的结果.从图7（b）还可以看出，在第2次到第9次的迭代偏差结果中，存在抛物面坐标局部偏差增大的现象，即呈现了“M”形误差，这与文献［16-18］通过试验得到薄膜由平面状态充气到理想抛物面时其变形为“M”形的结论一致.这种局部偏差增大现象的原因主要是所设定的边界条件，在分析时抛物面圆周固定，整个膜面沿抛物面径向的位移在该处被限定为0，由于结构的对称性，抛物面的中心径向位移也是0，而其他区域为自由状态.因此，当膜面受压力载荷时，整个膜面沿径向的位移集中在抛物面中心与圆周边界的区域内，在靠近边缘处，边界的影响较明显.随着迭代次数的增加，所得的设计抛物面形面与理想形面间的偏差逐步减小，具体表现为图7（b）中的曲线开始重合.随着迭代次数的增加，所得的平衡态形面与理想态抛物面间的“M”形偏差现象逐渐趋缓，这说明通过逆迭代来确定抛物面的初始形面是可行的，迭代过程中不断地将偏差作为回缩量施加给设计放样态形面，将会对下一次两形面间偏差值进行弱化.

图8所示为理想平衡态与设计平衡态的对比.其中，理想平衡态曲线为实际工作状态旋转抛物面的母线，初始态曲线为经过9次迭代所求得的抛物线初始状态曲线，以所求得的初始态曲线为母线进行旋转建模，并将设计气压施加于模型进行非线性求解，可得到设计平衡态曲线.由图8可知，求解后得到的平衡态（设计平衡态）与理想平衡态曲线几乎重合.因此，可以将此初始态作为放样态进行天线的组装，也可作为抛物面天线其他受力分析的起点.

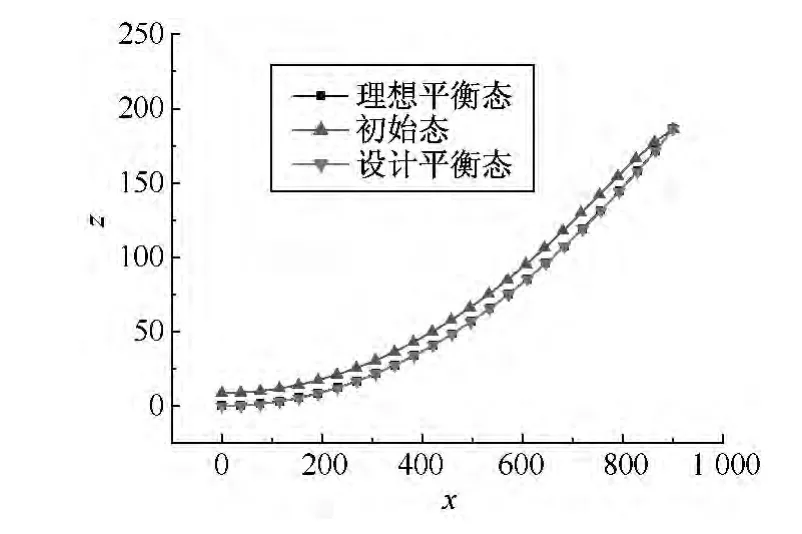
图8 理想平衡态与设计平衡态对比Fig.8 Comparison of ideal equilibrium and design equilibrium

4 结 语

（1）本文结合抛物面反射面常用的成形方式及其制作加工的可行性，探讨其初始形态确定的必要性.对于一个既定抛物面反射面，从设计图纸上能够确定抛物面天线工作时的几何参数和充气压的设计值，由最终工作时的形面、设计气压及边界条件确定抛物面的初始放样态，是抛物面天线组装时必不可少的一步.

（2）本文采用有限元软件ANSYS，利用逆迭代法来确定抛物面天线的初始形面.利用参数化语言APDL编制后处理程序，对分析过程中重要数据进行编辑，可以方便地处理抛物面天线初始形态确定的问题.

（3）使用逆迭代法可以保证抛物面反射面较高的形面精度.逆迭代法的效率较高，经过较少的迭代次数就可得到满足精度要求的结果.

［1］周益君，关富玲，钱利锋.球形陆基充气球天线：中国，201120011944.0［P］.2011-09-04.

［2］PRIEST R.Deployable satellite communication systems［EB／OL］.（2008-06-12）［2013-04-18］.http：／／www.gatr.com.

［3］PRIEST R.Inflatable antenna technology ［EB／OL］.（2008-06-12）［2013-04-18］.http：／／www.gatr.com.

［4］关富玲，钱利锋.新型陆基充气球天线力学分析与测试［J］.浙江大学学报：工学版，2012，46（2）：257-262.

［5］充气可展开天线用于应急通信［J］.军民两用技术与产品，2011（12）：33-34.

［6］吴昊.充气可展开反射面天线［D］.哈尔滨：哈尔滨工业大学电子与信息工程学院，2009：6-7.

［7］张林林.充气展开天线形面优化分析［D］.西安：西安电子科技大学机电工程学院，2011：15.

［8］李群辉.基于有限元平衡迭代法的充气膜结构找形分析［J］.山西建筑，2009，35（31）：52-53.

［9］夏劲松，关富玲，李刚.考虑面力度的力法找形和预应力精确确定［J］.应用力学学报，2005，22（3）：414-417.

［10］廖理，关富玲.索膜结构力密度法找形的一种离散方法［J］.空间结构，2003，9（3）：46-49.

［11］温世峰，支希哲.基于 Matlab的膜结构动力松弛法找形分析［J］.河南科技大学学报，2008，29（1）：65-67.

［12］李宗成，金康宁，刘春洋.能量优化法分析四边域膜结构初始形态［J］.华中科技大学学报，2002，19（3）：1-3.

［13］毛丽娜.充气膜结构反射面的形态分析与优化方法研究［D］.哈尔滨：哈尔滨工业大学航天学院，2010：51.

［14］李国强，沈黎元，罗永峰.索结构形状确定的逆迭代法［J］.建筑结构，2006，36（4）：74-76.

［15］DG／TJ08-2019—2007膜结构检测技术规程［S］.

［16］MARKER D K，JENKINS C H.Surface precision of optical membranes with curvature［J］.Optics Express，1997，1（11）：324-331.

［17］THOMAS M，VEAL G.Scaling characteristics of inflatable paraboloid concentrators ［J］.Journal of Solar Energy Engineering，1991，113（4）：353-358.

［18］PALLSOC A，THOMAS M.A comparison of the performance of seamed and unseamed inflatable concentrators［J］.Journal of Solar Energy Engineering，1995，117（2）：855-864.

Determination of the Initial Form of Spherical Ground-Based Inflatable Antenna Reflector

TANGYu-sia，JIANGJin-huaa，b，CHENNan-lianga，b

（a.College of Textiles；b.Engineering Research Center of Technical Textiles，Ministry of Education，Donghua University，Shanghai 201620，China）

The reflector model of spherical ground-based inflatable antenna was made by finite element software ANSYS and its APDL parametric language.The model was analyzed based on the characteristics of the reflector's boundary and its way under strain by inverse iteration method，after that，the initial form of the antenna's reflector was gotten.The results indicated that the inverse iteration method had a higher efficiency and an accurate initial form of reflector could be computed by a fewer iterations.

inflatable antenna；inverse iteration；equilibrium state；initial form

TS 101.8

A

2013-04-18

上海市优秀学术带头人计划资助项目（12XD1400400）；国家级大学生创新性实验资助项目（131025501）

唐渝思（1988—），女，四川南充人，硕士，研究方向为球形陆地用充气天线的制作.E-mail：tangshi713＠126.com

陈南梁（联系人），男，教授，E-mail：nlch＠dhu.ehu.cn

1671-0444（2014）03-0367-05