分数阶微分方程多点边值问题在共振条件下解的存在性

谢秀娟，寇春海，刘瑞娟

（东华大学a.理学院；b.信息科学与技术学院，上海 201620）

分数阶微分方程多点边值问题在共振条件下解的存在性

谢秀娟a，寇春海a，刘瑞娟b

（东华大学a.理学院；b.信息科学与技术学院，上海 201620）

研究了在共振条件下分数阶微分方程的多点边值问题，应用重合度理论，建立了关于解的存在性的充分条件.

分数阶微分方程；边值问题；重合度；共振

近年来，分数阶微分方程在控制、多孔介质、电化学、黏弹性力学等学科和工程领域得到了广泛的应用，已有大量文献研究了非线性分数阶微分方程的可解性［1-10］.文献［3］基于 Schauder不动点定理和Banach压缩映照原理，研究了如下形式的分数阶微分方程多点边值问题解的存在唯一性：

文献［7］考虑了如下分数阶微分方程的边值问题：

其中：2＜α≤3，1＜β＜2，0＜γ＜1，α-β-1＞0，0＜ξi＜1，ζi≥0，i＝1，2，…，m-2.利用重合度理论，建立了解的存在性的充分条件.

1 预备知识

本节给出文中将要用到的有关定义及结论.

定义 1.1［2］假 设f：R＋→R，f的α阶Riemann-Liouville分数阶积分定义为

其中：t＞0.这里假定右端积分存在.

定义 1.2［2］假 设f：R＋→R，f的α阶Riemann-Liouville分数阶导数定义为

其中：n＝［α］＋1，t＞0.这里假定右端积分存在.

由此很容易验证，当α＞0，μ＞-1时，函数tμ的 Riemann-Liouville分 数 阶 积 分 和 Riemann-Liouville分数阶导数具有如下形式：

引理1.1［6］假设α＞0，y∈C（0，1）∩L1［0，1］，则分数阶微分方程（t）＝0有如下解

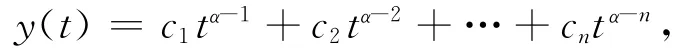
其中：ci∈R，i＝1，2，…，n，n＝［α］＋1.

其中：ci∈R，i＝1，2，…，n，n＝［α］＋1.

引理1.3［2］设α＞β＞0，t∈［0，1］，且y（t）∈L1［0，1］，则有

下面的定义和重合度理论是文中主要结论证明的基础.

定义1.3［4］设Y，Z为Banach空间，L∈B（Y，Z），称L为Fredholm算子，如果下列条件成立：（i）ImL是Z的闭集；（ii）dimKerL＜＋ ∞；（iii）codim ImL＜＋∞.规定L的指标为indL＝dimKerL-codim ImL，当dimKerL＝codim ImL时，称L为指标是0的Fredholm算子.

由定义可知，存在连续投影算子P：Y→Y及Q：Z→Z使得

Y＝KerL⊕KerP，Z＝ImL⊕ImQ及L｜domL∩KerP：domL∩KerP→ImL是可逆的，记其逆算子为K P：ImL→domL∩KerP.广义逆算子K P，Q：Y→domL∩KerP，K P，Q＝K P（I-Q）.

定义1.4［4］设L：domL⊂Y→Z为Fredholm算子，Ω为Y中的有界开集，N为Ω→Z的算子，称N在Ω上是L-紧的，如果QN：Ω→Z有界且K P，QN：Ω→Y在Ω上是紧的.

当ImQ同构于KerL时，存在同构映射J NL：ImQ→KerL，并有如下的重合度定理.

定理1.1［11］设L为指标是0的Fredholm算子，N在Ω-上是L-紧的，其中Ω为Y中的有界开集.假设满足下列条件：

（1）对 ∀（y，λ）∈ ［（domL＼KerL）∩∂Q］×（0，1），有Ly≠λNy；

（2）对 ∀y∈KerL∩∂Q，有Ny∉ImL；

（3）deg（J NLQN｜KerL，Ω∩KerL，0）≠0，其中Q：Z→Z是连续投影且ImL＝KerQ，其中J NL：ImQ→KerL是同构映射.

则方程Ly＝Ny在domL∩中至少存在一个解.

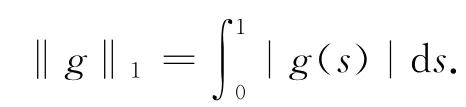
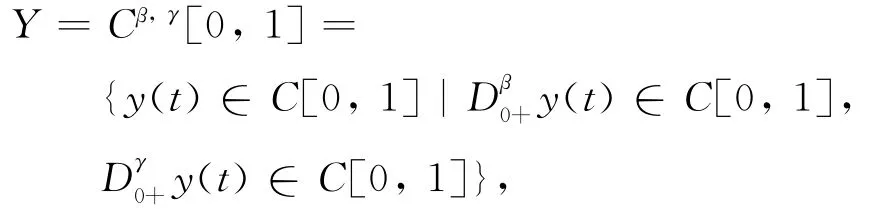
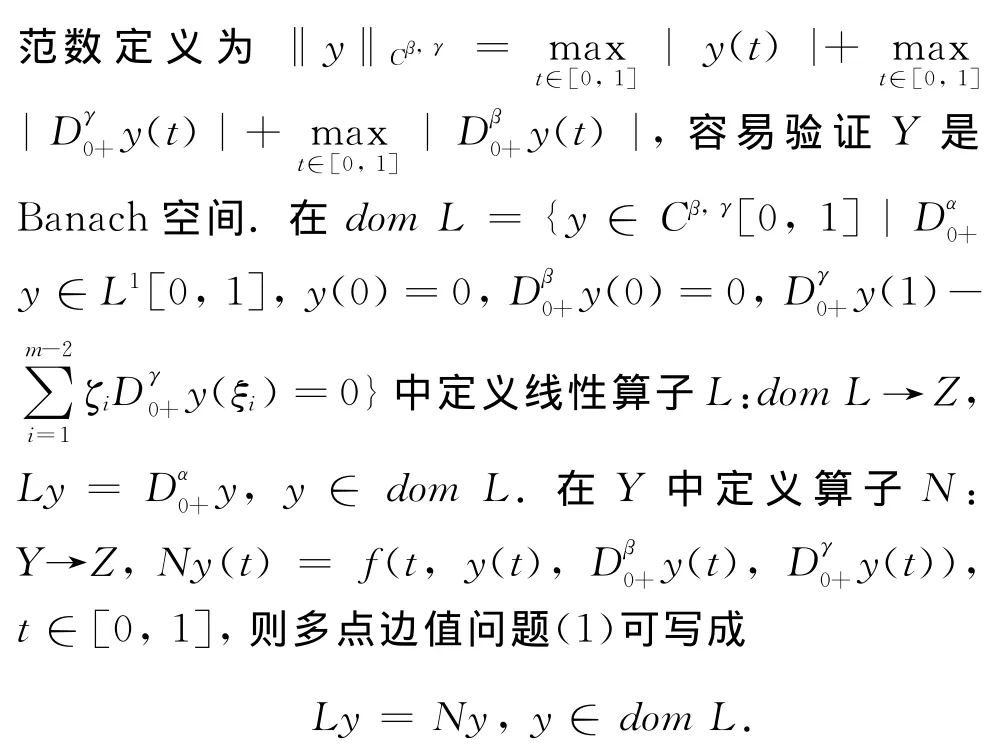
引理1.4［7］F⊂Cβ，γ［0，1］是相对紧集，当且仅当F一致有界且等度连续，即存在M＞0，使得对∀y∈F，有

且对 ∀ε＞0，∃δ＞0，∀t1，t2∈ ［0，1］，｜t1-t2｜＜δ，∀y∈F，有

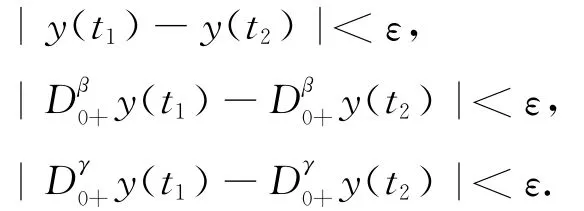
定义 1.5［4］设f：［0，1］×R3→R 满 足Carathéodory条件，假设下列条件成立：

（1）对∀（x，y，z）∈R3，函数t→f（t，x，y，z），t∈［0，1］是Lebesgue可测的；

（2）对几乎所有的t∈［0，1］，函数t→f（t，x，y，z）在R3上连续；

（3）对∀r＞0，∃φr（t）∈L1［0，1］，使得对t∈［0，1］，（x，y，z）∈R3（‖（x，y，z）‖≤r），｜f（t，x，y，z）｜≤φr（t）几乎处处成立，其中‖·‖为R3中的范数.

2 主要结论

本节建立含Riemann-Liouville分数阶导数的分数阶微分方程共振多点边值问题解的存在性定理，为证明主要结论，需要下面的引理.

的解当且仅当y满足

且

证明 先证必要性.假设y∈Y是边值问题（3）和（4）的解，对式（3）两边求α阶积分，

由引理1.2有

再证充分性.假设式（5）和（6）成立，由引理1.2，容易验证y是BVP式（3）和（4）的解.

引理2.2L为指标是0的Fredholm算子，且

建立映射Q：Z→Z，

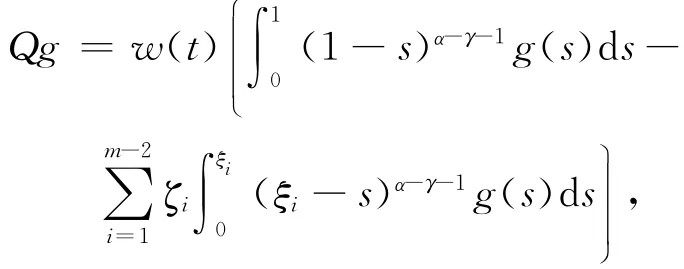
又dimKerL＝1＝dim ImQ＝codim ImL＜＋∞，且ImL⊂Z为闭集.故L为指标是0的Fredholm算子.

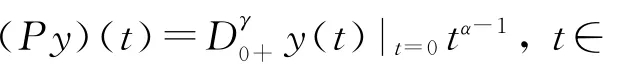
考虑映射K P：ImL→domL∩KerP：

注意到（K PL）y＝K P（Ly）＝y，∀y∈domL∩KerP，（LK P）g＝L（K Pg）＝g，∀g∈ImL.因此，K P＝（L P）-1，其 中L P＝L｜domL∩KerP：domL∩KerP→ImL.

引理2.3 假设2＜α≤3，1＜β＜2，0＜γ＜1，且α-β-1＞0，对∀g∈ImL，

其中

证明 对∀g∈ImL，t∈［0，1］，有

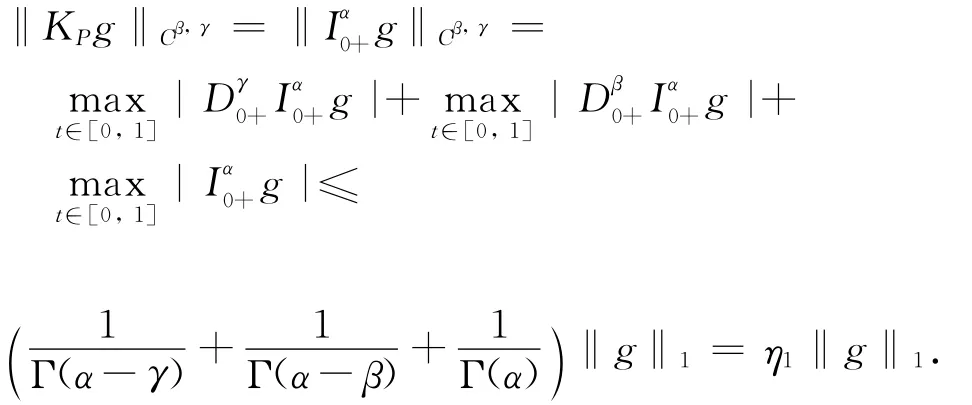
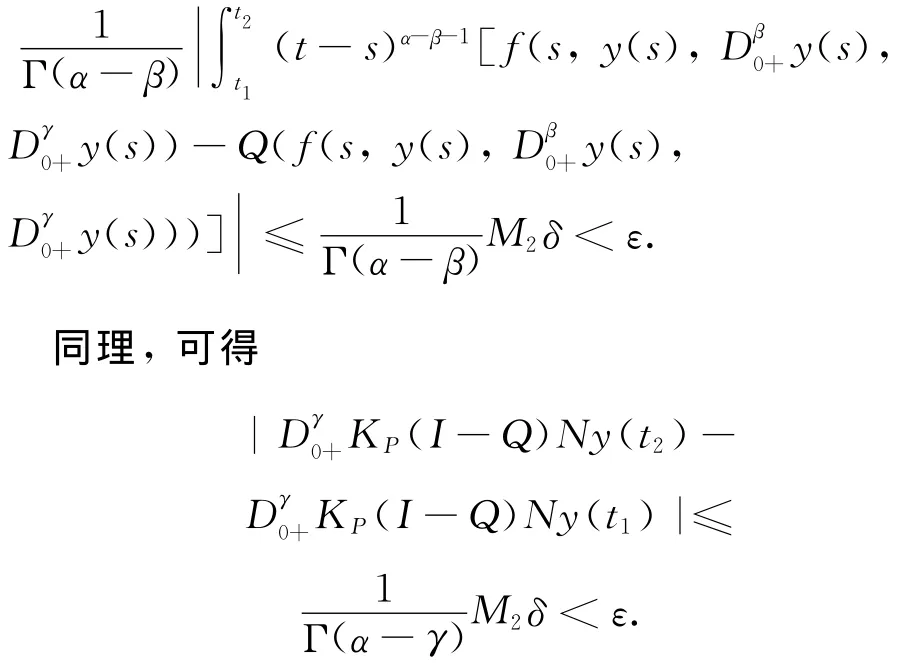
由以上可知，K P（I-Q）N：Y→Y是全连续的.

H1存在函数β1，β2，β3，β4∈C［0，1］，且βi（t）≥0（i＝1，2，3，4）对t∈［0，1］几乎处处成立，对t∈［0，1］，（x，y，z）∈R3，有

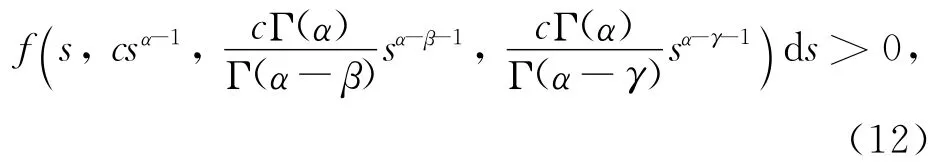
则边值问题（1）在domL上至少存在一个解.

证明 证明分为4步.

第1步：令Ω1＝｛y∈domL＼KerL｜Ly＝λNy，λ∈［0，1］｝，则Ω1是有界的.

事实上，任取y∈Ω1，则y∈domL＼KerL，且Ly＝λNy，故λ≠0，且Ny∈ImL＝KerQ⊂Z，则Q（Ny）＝0.由 H3知，∃t0∈［0，1］，使得

由引理2.3，有

由H1，对∀y∈Ω1，有

即Ω1是有界的.

第2步：令Ω2＝｛y∈KerL｜Ny∈ImL｝，可以证明Ω2是有界的.设y∈Ω2，则

由Ny∈ImL，有

由 H4，有｜c｜≤S，即得Ω2是有界的.

第3步：若式（11）成立，则令

若式（12）成立，则令

其中J NL：ImQ→KerL是线性同构，J NL（cw（t））＝ctα-1，∀c∈R，t∈［0，1］.可证Ω3是有界的.不妨设式（11）成立，则

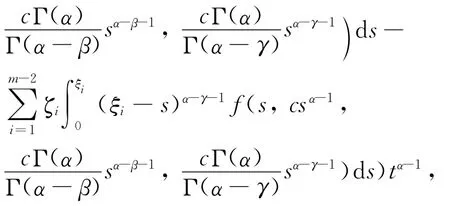
矛盾，所以｜c｜≤S.即证得Ω3是有界的.

根据引理2.4，由QN（）有界，且K P，QN＝K P（IP）N：Ω-→Y是紧的，可知N是L-紧于的.则由第1步和第2步，有

（1）对 ∀（y，λ）∈ ［（domL＼KerL）∩∂Ω］×（0，1），有Ly≠λNy；

（2）对 ∀y∈KerL∩∂Ω，有Ny∉ImL；

定义H（y，λ）＝-λIy＋（1-λ）J NL QNy，其中I为Y中的恒等映射，由第3步可知，对∀y∈KerL∩∂Ω，有H（y，λ）≠0，因此，由拓扑度的同伦性质，有

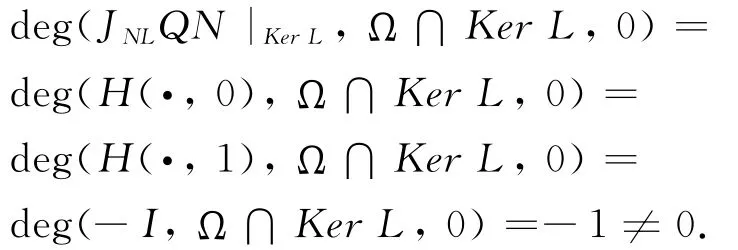
即验证了定理1.1的条件（3）.根据定理1.1，可得边值问题（1）在domL∩上至少存在一个解.

注：上述证明方法可以推广应用于研究下面分数阶微分方程多点边值问题解的存在性：

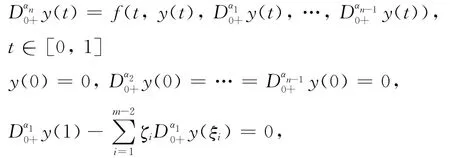
其中：n-1＜αn≤n，j-1＜αj＜j，αn-αn-1-1＞0，0＜ξi＜1，ζi≥0，i＝1，2，… ，m-2，j＝1，2，…，n-1.

［1］KILBAS A A，SRIVASTAVA H M，TRUJILL J J.Theory and applications of fractional differential equations［M］.Amsterdam，Holland：Elsevier，2006.

［2］PODLUBNY I.Fractional differential equations［M］.London：Academic Press，1999.

［3］REHMAN M，KHAN R A.Existence and uniqueness of solutions for multi-point boundary value problems for fractional differential equations［J］.Applied Mathematics Letters，2010，23（9）：1038-1044.

［4］CHEN Y，TANG X H.Solvability of sequential fractional order multi-point boundary value problems at resonance［J］.Applied Mathematics and Computation，2012，218（14）：7638-7648.

［5］FERANCO D，NIETO J J，OREGAN D.Existence of solutions for first order ordinary differential equations with nonlinear boundary conditions［J］.Applied Mathematics and Computation，2004，153：793-802.

［6］AHMAD B，NIETO J J.Existence results for a coupled system of nonlinear fractional differential equations with three-point boundary conditions［J］.Computers and Mathematics with Applications，2009，58（9）：1838-1843.

［7］BAI Z B.Solvability for a class of fractional m-point boundary value problem at resonance［J］.Computers and Mathmatics with Applications，2011，62（3）：1292-1302.

［8］DU Z J，LIN X J，GE W G.Some higher-order multi-point boundary value problem at resonance ［J］. Journal of Computational and Applied Mathematics，2005，177（1）：55-65.

［9］ZHOU H C，KOU C H，XIE F.Existence of solutions for fractional differential equations with multi-point boundary conditions at resonance on a half-line［J］.Electionic Journal of Qualitative Theory of Differential Equations，2011，27：1-16.

［10］JIANG W H.Solvability for a coupled system of fractional differential equations at resonance［J］.Nonlinear Analysis：Real World Applications，2012，13（5）：2285-2292.

［11］MAWHIN J.Topological degree and boundary value problems for nonlinear differential equations［M］／／Topological Methods for Ordinary Differential Equations Lecture Notes in Mathematics.Berlin：Springer，1991，1537：74-142.

Existence of Solutions for m-Point Boundary Value Problem for Fractional Differential Equations at Resonance

XIEXiu-juana，KOUChun-haia，LIURui-juanb

（a.College of Science；b.College of Information Science and Technology，Donghua University，Shanghai 201620，China）

A m-point boundary value problem of fractional differential equations at resonance is studied.A suf ficient condition for the existence of solutions of the above problem is established by using the coincidence degree theory.

fractional differential equation；boundary value problem；coincidence degree；resonance

O 175.8

A

2013-05-20

上海市自然科学基金资助项目（10ZR1400100）

谢秀娟（1988—）女，湖北咸宁人，硕士研究生，研究方向为分数阶微分方程.E-mail：xiyanyixian＠126.com

寇春海（联系人），男，教授，E-mail：kouchunhai＠dhu.edu.cn

1671-0444（2014）03-0372-07