针对离散私钥比特泄漏的RSA格攻击方法

刘向辉，韩文报，王 政，权建校

针对离散私钥比特泄漏的RSA格攻击方法

刘向辉1,2，韩文报1,2，王 政1,2，权建校3

(1. 解放军信息工程大学四院，郑州 450002；2. 数学工程与先进计算国家重点实验室，郑州 450002； 3. 江南计算技术研究所，江苏 无锡 214083)

RSA算法是目前应用最广泛的公钥密码体制之一，而格攻击是针对RSA体制的一类重要攻击方法。为此，将RSA算法的部分私钥泄漏问题转化为多变元线性同余方程的求解问题，基于同余方程构造出特定的格，利用LLL格基约化算法进行约化，从而以一定的概率求得同余方程的小根。以上述多变元线性同余方程的小根求解技术为基础，提出一种针对离散私钥比特泄漏的RSA格攻击方法。在该方法下，如果RSA算法的公钥参数=N≤1/2，并且私钥的未知部分N≤1/2–β，则能以高概率恢复出RSA算法的私钥。通过NTL包对长度为1 024 bit的大整数进行实验，结果验证了该攻击方法的有效性。

RSA算法；格攻击；离散私钥比特泄漏；线性同余方程；小根；格基约化算法

1 概述

自1976年公钥密码的思想提出以来，各种公钥密码体制不断涌现，但公认安全的且应用广泛的却并不多，其中较著名的是RSA公钥密码体制、ElGamal公钥密码体制和椭圆曲线公钥密码体制。而RSA公钥密码体制由于具有简单易用、明密文长度相同等优点，在各种秘密通信中得到广泛应用，一直是公钥密码学研究的热点[1]。一般来讲，公钥密码体制往往利用数学中已经得到证明的难题或公认的难题来设计方案，RSA算法就是建立在大数分解问题上的。目前，针对大数分解问题最好的通用攻击算法是一般数域筛法，它是一个亚指数时间算法，在当前的计算能力下无法对实际使用的RSA模数进行分解。也就是说，在不借助其他条件下直接通过大数分解对RSA体制进行攻击是困难的。

然而，在实际使用过程中可能会泄漏RSA体制的部分信息，例如泄漏私钥或者的若干比特信息。同时，由于旁道攻击等手段的发展，攻击者往往能够获得部分密钥信息。如何利用这些已知信息对RSA体制进行攻击成为密码学的一个重要研究课题。文献[2-3]提出利用LLL算法求解整系数同余方程及多项式方程小根的方法，此后该方法被广泛应用于RSA算法的私钥泄漏攻击中，例如，在泄漏私钥的低/4比特，同时加密指数较小的条件下RSA的私钥恢复[4]；在加密指数较大情况下的RSA部分私钥泄漏攻击等[5]；私钥指数的连续比特泄漏攻击等[6]。

早期的RSA私钥泄漏攻击都建立在文献[2-3]求解多变元模方程或者求解多变元多项式方程小根的基础上，主要集中在私钥的高位连续比特或者低位连续比特泄漏的情形。在实际环境中，攻击者获得的部分私钥信息通常是不连续的，特别是旁道攻击[7]的存在使得RSA体制离散比特私钥泄露攻击也显得更有意义。文献[8]通过构造多变元线性模方程并利用格基约化算法进行求解，提出针对泄漏私钥部分离散比特的攻击方法，在泄漏私钥的70%比特信息的条件下该方法能够有效分解RSA的模数。文献[9]利用变换多项式的格构造方法给出针对私钥指数的离散比特泄漏攻击，但该方法要求格的维数较高。

本文通过构造多变元线性模方程，并利用典型的格构造方法，针对RSA算法私钥部分离散比特泄漏的情况进行分析。在公钥指数较小的条件下，如果泄漏私钥的部分离散比特，则可以有效恢复出RSA算法的私钥参数。

2 准备知识

本节给出RSA格攻击所用到的基础知识，包括格的基本概念、Minkowski定理等格的基本理论以及LLL算法等格基约化算法，具体细节可参考文献[10]。

显然，一个格有多组基，在解决格上相关问题时，希望能找到一组特定的基有利于问题的解决，寻找这组基的过程就称为格基约化，这组基就称为约化基。拥有长度较短向量的基往往具有一些良好的性质，如何寻找具有短向量的基一直受到人们的关注。定理1给出了格中最短向量长度的上界。

3 一种离散私钥比特泄漏的RSA格攻击方法

本节根据RSA算法的已知信息建立多变元线性同余方程，并利用格基约化算法对方程进行求解，从而给出离散私钥比特泄漏的RSA格攻击方法。

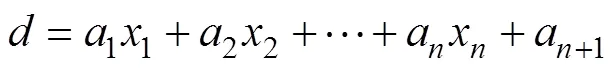
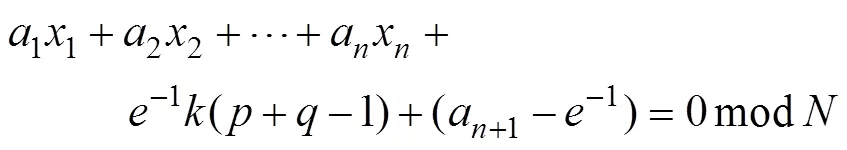
方程的解为：

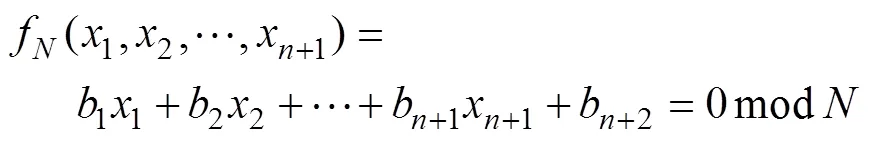
对于一般的多变元线性同余方程，解的个数以及解的结构是一个较困难的问题，但是在某些限定条件下，能够得到上述同余方程的唯一解。定理2给出了一种求解情况，能够在一些限定条件下完成对RSA算法私钥的恢复。

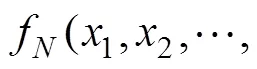
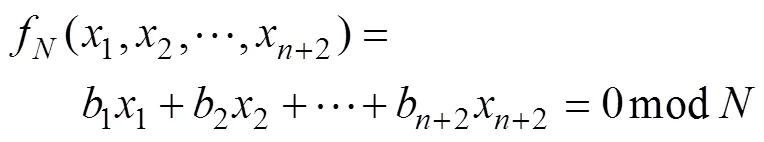
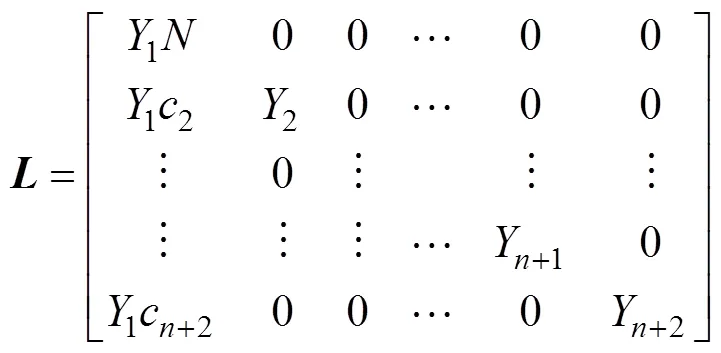
易求格的范数为：

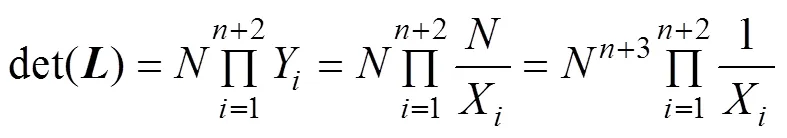
注释1 在证明过程中，省略小常数3，这是因为常数3相对于非常微小。如果是一个1 024 bit的大整数，小常数影响的指数为0.00 155，而且它并不随着攻击算法参数的改变而改变。于是为了计算方便，通常忽略这些小常数，并且它基本不影响攻击算法的结果。

注释2格基约化算法通常采用LLL算法，它是一个多项式时间算法，这样能够在多项式时间内完成攻击，而且LLL算法往往能够得到需要的短向量。

注释3定理2描述的攻击方法是一个概率算法。也就是说，如果满足已知条件，该方法并不能保证一定可以恢复出私钥。但实际结果表明，该方法往往能够得到方程的解并恢复出私钥。

根据上述描述及定理2的证明，给出如下针对离散私钥比特泄漏的RSA格攻击算法。

算法离散私钥比特泄漏的RSA格攻击算法

(2)根据定理2的证明对方程进行变换并构造格；

(3)利用LLL算法求取格中的短向量；

(4)对短向量进行代入计算出原始方程的解；

(5)输出私钥未知比特块的值。

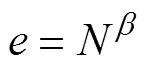
4 实验结果与分析

本文算法能够有效恢复出离散私钥比特泄漏情形的私钥，本节对攻击方法进行实现，给出了部分实验结果。

实验采用Intel Core2 Duo CPU E7500 2.93 GHz、2 GB内存、Windows XP操作系统、C++编程语言、Visual Studio 2005编程环境。实验基本数据类型以及部分函数使用NTL包5.5.2版本[12]。

随机产生1 024 bit的大整数如下：

=89884656743115795386465259539451236680898848947115328636715040578866337902750481566354238661203768010560056939935696678829394884407208445324503014745709298151367448461125728029121649765323616136679383490070243049322387623086994912866587628961575922009245120828003518545377059539890024051847723277345174851613

选择公钥参数=65 537，并计算其私钥参数：

=74675981359372092515712657756748721101081534514435134559284992133269975222072389952619979349454853909073866369617449879745836591028025167936105408347565173424220906961557338958448600530303116223128214181994791463002504381615405570121172373758673816534516868922306693487189599921278285735907955687259234560833

为描述方便，以下运算选择16进制表示。私钥参数的16进制表示为：

=6a5795a86a5795a86a5795a86a5795a86a5795a86a5795a86a5795a86a5795a86a5795a86a5795a86a5795a86a5795a86a5795a86a5795a8dda37444610e8ebd0bd2f42d0bd2f42d0bd2f42d0 bd2f42d0bd2f42d0bd2f42d0bd2f42d0bd2f42d0bd2f42d0bd2 f42d0bd2f42d0bd2f42d0bd2f42d0bd2f44e5fc14d425cb6eb41

显然是一个1 024 bit的大整数。根据定理2，如果私钥的未知比特数小于490 bit，那么可以恢复私钥。下文分2种情况进行实验验证。

情况1私钥单未知比特块未知。假设的第101比特~第580比特未知，也即：

=6a5795a86a5795a86a5795a86a5795a86a5795a86a5795a86a5795a86a5795a86a5795a86a5795a86a5795a86a5795a86a5795a86a5795a************************************************************************************************************************d0bd2f44e5fc14d425cb6eb41

其中，*表示未知部分。那么可以建立一个双变元的方程，然后构造3变元的格对其进行求解，运行LLL算法恢复出私钥的未知比特。

情况2私钥多比特块未知。选取5个比特块未知，假设的第101比特~第180比特，第257比特~第356比特，第457比特~第556比特，第657比特~第756比特，第857比特~第956比特共480个比特信息未知，也即此时：

=6a5795a86a5795a86*************************5795a86a5795a86a5795a86a5*************************95a86a5795a86a5795a8dda37*************************2d0bd2f42d0bd2f42d0bd2f42*************************0bd2f42d0bd2f42d0bd********************d0bd2f44e5fc14d425cb6eb41

其中，*表示未知部分。那么可以建立一个6变元的方程，然后构造7变元的格对其进行求解，运行LLL算法恢复出私钥的未知比特。

通过上述2个实验，本文算法能够有效恢复出RSA算法的私钥，并且由于算法使用的格非常小，整个攻击过程在普通PC机上即可完成。

5 结束语

随着旁道攻击等物理攻击手段的不断发展，RSA算法的私钥泄漏攻击越来越受到人们的重视。但是，由于离散比特的私钥泄漏攻击列方程及解方程的困难性，目前研究大多集中于泄漏私钥的连续比特。本文对离散私钥比特泄漏情形的RSA安全性进行了初步分析，利用多变元线性同余方程的典型求解算法，给出一种针对离散私钥比特泄漏的RSA格攻击方法。利用该方法攻击者可以有效恢复RSA算法的私钥参数。另一方面，本文分析结果还可以指导RSA算法在使用时选取安全的参数。然而，本文结果要求已知RSA算法有较多的私钥比特，同时利用基本的格构造方法，虽然构造格的维数比较低，格基约化运算部分用时较少，但是该方法是概率性的，可能会有不成功的情形存在。因此，如何对本文方法进行改进是下一步研究的重点。

[1] Rivest R, Shamir A, Adleman L. A Method for Obtaining Digital Signatures and Public Key Cryptosystems[J]. Communications of the ACM, 1978, 21(2): 120-126.

[2] Coppersmith D. Finding a Small Root of a Univariate Modular Equation[C]//Proceedings of EUROCRYPT’96. Berlin, Germany: Springer-Verlag, 1996: 155-165.

[3] Coppersmith D. Finding a Small Root of a Bivariate Integer Equation Factoring with High Bits Known[C]//Proceedings of EUROCRYPT’96. Berlin, Germany: Springer-Verlag, 1996: 178-189.

[4] Blomer J, May A. New Partial Key Exposure Attacks on RSA[C]//Proceedings of CRYPTO’03. Berlin, Germany: Springer-Verlag, 2003: 27-43.

[5] Ernst M, Jochemsz E, May A. Partial Key Exposure Attacks on RSA up to Full Size Exponents[C]//Proceedings of EUROCRYPT’05. Berlin, Germany: Springer-Verlag, 2005: 371-386.

[6] Santanu S. Some Results on Cryptanalysis of RSA and Fac- torization[D]. Kolkata, Indian: Indian Statistical Institute, 2011.

[7] 陈财森, 王 韬, 郑媛媛, 等. RSA公钥密码算法的计时攻击与防御[J]. 计算机工程, 2009, 35(2): 123-125.

[8] Herrman M. Solving Linear Equations Modulo Divisors: On Factoring Given Any Bits[C]//Proceedings of ASIACRYPT’08. Berlin, Germany: Springer-Verlag, 2008: 406-424.

[9] 刘向辉, 韩文报, 孙 杰. 基于离散比特的RSA私钥泄漏攻击[J]. 信息工程大学学报, 2012, 13(4): 385-388.

[10] Nguyen P Q, Valle B. The LLL Algorithm: Survey and Applications[M]. Berlin, Germany: Springer Publishing Company, 2009.

[11] Lenstra A K, Lenstra H W, Lovasz L. Factoring Polynomials with Rational Coefficients[J]. Mathematiche Annalen, 1982, 261(4): 515-534.

[12] Shoup V. Number Theory Library(NTL) for C++[EB/OL]. (2010-05-16). http://www.shoup.net/ntl/.

编辑 陆燕菲

RSA Lattice Attack Method for Discrete Private Key Bit Leakage

LIU Xiang-hui1,2, HAN Wen-bao1,2, WANG Zheng1,2, QUAN Jian-xiao3

(1. The Fourth Institute, PLA Information Engineering University, Zhengzhou 450002, China; 2. State Key Laboratory of Mathematical Engineering and Advanced Computing, Zhengzhou 450002, China; 3. Jiangnan Institute of Computing Technology, Wuxi 214083, China)

RSA algorithm is one of the most widely used public key cryptosystems at present and lattice attacks play an important role for the analysis of RSA system. The problem of partial discrete private key bit leakage is transformed into the solution of multivariate linear congruence equations and a special lattice is constructed. And then by the lattice reduction algorithms such as LLL algorithm, the small roots of multivariate linear congruence equations can be obtained with a high probability. Based on the above technology, this paper proposes a lattice attack method on RSA for discrete private key bit leakage. With this method, if the public parameter satisfies=N≤1/2and the unknown part of private keysatisfiesN≤1/2–β, it can recover the private keywith a high probability. The experiment on 1 024 bit number is given with NTL package and the results verify the availability of the attack method.

RSA algorithm; lattice attack; discrete private key bit leakage; linearcongruence equation; small root; lattice base reduction algorithm

1000-3428(2014)03-0163-04

A

TN918

国家自然科学基金资助项目(61003291)；数学工程与先进计算国家重点实验室开放基金资助项目(2013A03)。

刘向辉(1984－)，男，博士研究生，主研方向：密码学，信息安全；韩文报，教授、博士、博士生导师；王 政，副教授、博士；权建校，助理研究员、硕士。

2013-03-07

2013-04-07 E-mail：lxhkz2002@163.com

10.3969/j.issn.1000-3428.2014.03.033