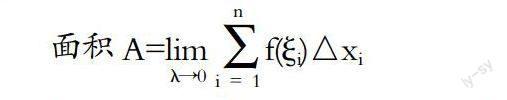高等数学教学过程中学生发展能力的培养

【摘要】当前高职院校忽视学生“发展能力”的培养，没有建立“自我学习、终身学生”的现代教育观。笔者认为发展能力主要包括：学习新知识能力、做事能力和做事态度。提出在数学定义教学中注重培养学生发展能力，在知识应用教学中培养学生做事态度。

【关键词】数学思想 数学方法 发展能力

【中图分类号】O13 【文献标识码】A 【文章编号】2095-3089（2014）09-0143-02

当前的高职院校在教学中重知识、技能的传授、积累，忽视学生“学习能力”的培养，没有建立起“自我学习、终身学习”的现代教育观。结果是高职院校学生毕业后上手快，上岗竞争时有优势，但是基本功（数学、英语、自学能力）不足，随着形势的变化、技术的更新，需要在工作岗位上自我学习时，可能就落在别人后面。这就叫做“好用、不经用”，可持续发展能力不足[1]。

作为高职学校的数学老师，要在了解学生“短处”的同时，更要了解学生的长处，了解学生的需求点，引导学生建立学习目标，增强学生的学习自信心。要不断更新职业教育的观念，树立多元智能观、多元人才观、多元成功观，按照职业教育特点和认知规律设计课程和安排教学。不但要教学生学习知识，更要教学生做事的态度和学习数学家们解决问题的思想和方法，以达到提高学生学习能力的目的。笔者认为发展能力主要包括：学习新知识能力、做事能力和做事态度。现就笔者在高等数学课程教学中的一些做法予以介绍。

1.在定义教学中注重培养学生学习能力

通过教学让学生知道数学定义就是把解决实际问题中的数学思想抽象出来的。很多专业的概念也是这样形成的，一些政策法规也是从实际中总结出来的。

1.1 先求曲边梯形面积的近似值

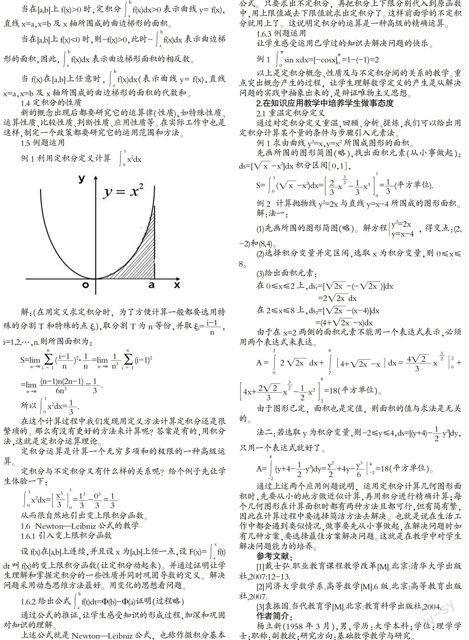
设y=f（x）在[a，b]上非负且连续，由直线x = a，x = b，y = 0及曲线y=f（x）所围成的图形，称为曲边梯形。求曲边梯形的面积的近似值。把曲边梯形分成若干个小的曲边梯形，每个小的曲边梯形可用矩形近似计算，以此求得曲边梯形的面积的近似值。

给出f（x）=sinx，a=0，b=？仔，对区间[a，b]进行n等分，求曲边梯形面积的近似值An（由学生完成）。用excel计算An得出：n=5， An=1.933 856；n=10，An=1.983 598；n=20， An=1.995 952 32；n=50，An=1.999 403 862.

大家发现小曲边梯形越多，整个曲边梯形的面积就越向一个值2靠近。怎样才能达到精确值呢？那就是小曲边梯形无限多，运用极限就能求出精确值。数学家就把这种解决实际问题中的精华抽象出来形成数学概念，从而引出定积分的定义。

1.2 定积分的定义（理论来源于实践）

由上述例子可见，它是解决一个函数与其自变量的增量积的无穷多项和的问题。它们的计算方法与步骤是分割、作积、求和、求极限。

2.在知识应用教学中培养学生做事態度

2.1 重温定积分定义

通过对定积分定义重温，回顾、分析、提炼，我们可以给出用定积分计算某个量的条件与步骤引入元素法。

例1 求由曲线y2=x，y=x2所围成图形的面积。

通过上述两个应用例题说明，运用定积分计算几何图形面积时，先要从小的地方做近似计算，再用积分进行精确计算；每个几何图形在计算面积时都有两种方法且都可行，但有简有繁，因此在计算过程中要选择简洁方法去解决。也就是说在生活工作中都会遇到类似情况，做事要先从小事做起，在解决问题时如有几种方案，要选择最佳方案解决问题。这就是在教学中对学生解决问题能力的培养。

参考文献：

[1]戴士弘.职业教育课程教学改革[M].北京：清华大学出版社，2007：12-13.

[2]同济大学数学系.高等数学[M].6版.北京：高等教育出版社，2007.

[3]袁振国.当代教育学[M].北京：教育科学出版社，2004.

作者简介：

杨立新（1958年3月），男，学历：大学本科；学位：理学学士；职称：副教授；研究方向：基础数学教学与研究。