三元阵被动定位中时延差估计算法研究
郑恩明 丘 颜 孙长瑜 陈新华
三元阵被动定位中时延差估计算法研究
郑恩明*①②丘 颜③孙长瑜①陈新华①
①(中国科学院声学研究所 北京 100190)②(中国科学院大学 北京 100190)③(91388部队 湛江 524022)

信息处理技术;被动定位;时延差估计
1 引言

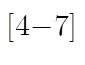
文献[13]提出用信号间互功率谱来估计时延差互谱法,但在实际应用中,单独采用互谱法会存在相位模糊问题,鲁棒性较差,时延差估计精度鲁棒性差[14,15]。为了增强互谱法在实际应用中的鲁棒性,提高时延差估计精度,本文对互谱法进行改进,以解决单独采用互谱法进行时延差估计存在的相位模糊问题,增强互谱法在实际应用的鲁棒性。改进算法所得时延差由周期值和修正值构成;时延差周期值是通过对阵元间互谱信号进行时延补偿所得,时延差修正值是采用最小二乘法对补偿后互谱信号拟合所得。理论分析和实验结果表明:该方法可以获得高精度的时延差,且具有较好的实用性,可以有效提高三元阵被动定位精度。
2 三元阵被动定位模型
由图1及三元阵被动测距法可得目标相对三元阵的方位和距离估计为

3 基于相位补偿的时延差估计算法
为了增强互谱法在实际应用中的鲁棒性,本文首先对阵元间互功率谱进行相位补偿,然后按互谱法进行时延差估计。改进算法所得时延差包含两部分:一部分为经相位补偿所得的周期值,另一部分为经相位补偿后所得修正值,算法原理如下。

图1 三元阵被动定位模型
3.1 算法基本原理
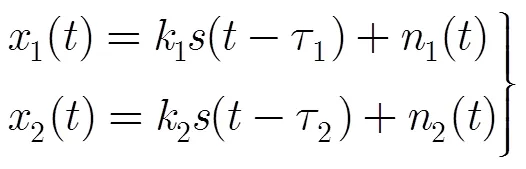
根据上文所述,首先按式(3)对阵元1,阵元2接收信号做快速傅里叶变换:

由式(3)结果可得阵元1,阵元2互功率谱为[12]
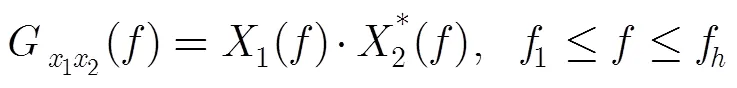

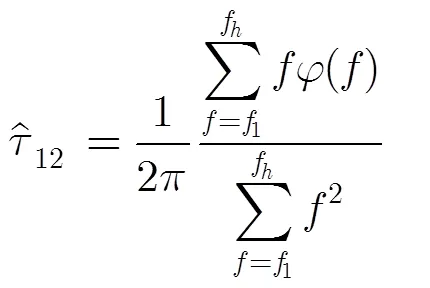

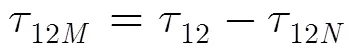
至此,可按式(9)求取无相位模糊的相位函数。
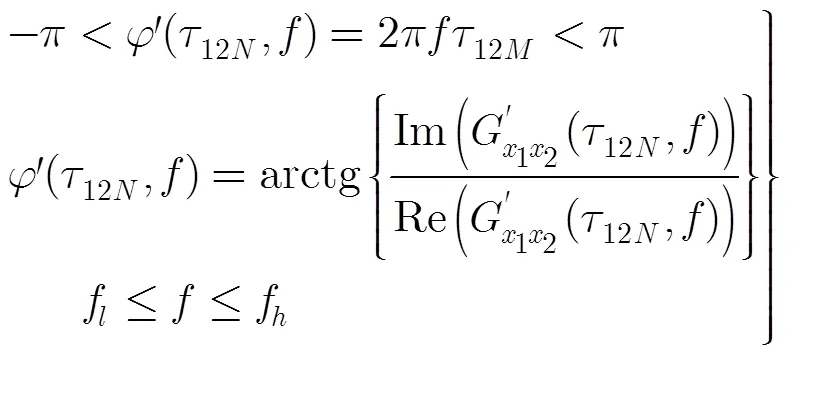
最后将时延差周期值和时延差修正值相加即可得到时延差估计值。

3.2 算法实现
图2为本文算法具体流程,虚线框内为算法创新部分。算法实现分为如下5个步骤:

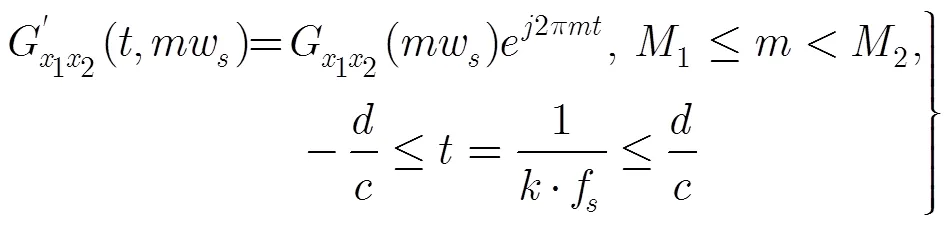
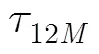
4 改进时延差估计算法性能分析
4.1 相位模糊分析[2]


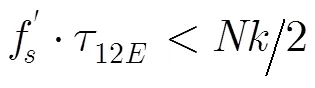
4.2 运算量分析
本文方法只需对频带内数据进行相位补偿即可完成时延差周期值估计,但由于本文方法在相位补偿过程中采用类内插方法缩小了相位补偿时所需的时间间隔,从而增加了部分运算量。相比频域无插值法,本文方法增加的运算量主要包括:

图2 改进时延差估计算法流程图
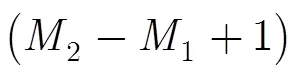
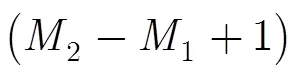
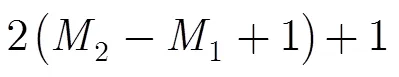
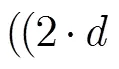
(5)最后时延差周期值与修正值相加,增加了一次实加法。
4.3 误差分析
根据文献[1]可知,本模型时延差估计标准差的克拉美-罗(Cramer-Rao)下界为



此时,可得

式(18)即为不同信噪比下的被动声呐时延差估计标准差的克拉美-罗下界[1,16,17]。

由图3可知:
(1)相比常规无插值法,二次样条插值法突破了采样率的限制,时延差估计精度得到了有效提高,但该方法受峰值局部限制,估计精度提高不多;
(2)相比常规无插值法,ZOOM-FFT法突破了采样率限制,时延差估计精度也得到了有效提高;且与二次样条插值法相比,ZOOM-FFT法不再受峰值局部限制,时延差估计精度得到进一步提高;

5 实验分析
5.1 仿真分析


5.2 海试数据处理

图3 高斯噪声下不同方法时延差估计误差标准差

图4 阵元1,阵元2时延差估计结果
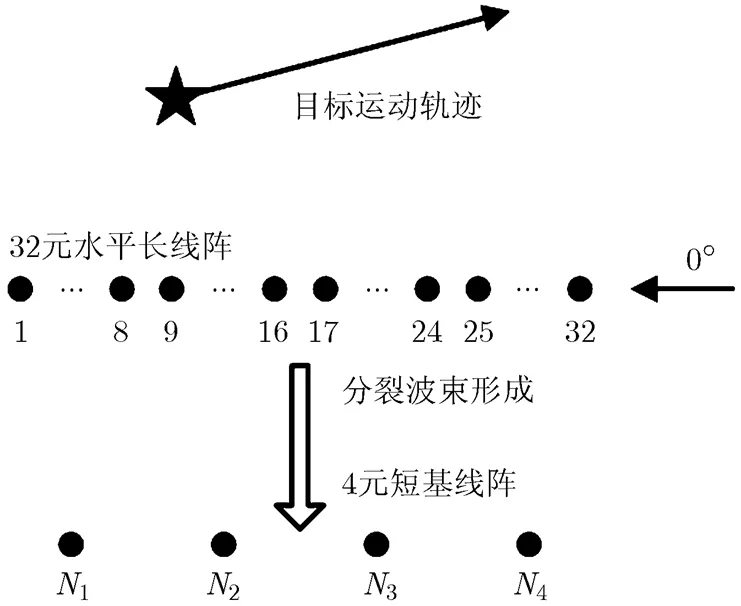
图5 实验水平线阵及目标运动轨迹图
由图7可知,两种方法对海试数据的处理结果与5.1节所得的数值仿真结果类似,常规无插值法受采样率限制,时延差估计值同样出现反复跳变,时延差估计精度误差比较大;本文方法结合了内插法和互谱法的优点,突破了采样率的限制,使时延差估计值精度得到有效提高,时延差估计值不再出现反复跳变。
6 结论

但本文方法需要对阵元间互功率谱进行相位补偿,其要求各阵元与滤波放大器之间的相位一致性较好,所以在实际应用中,首先需要校准并补偿各通道的相位,然后再采用本文方法求取高精度的时延差估计值。

图6 波束形成所得方位历程图

图7 基元,时延差估计结果
[1] 李启虎. 声呐信号处理引论[M]. 第2版, 北京: 海洋出版社, 2000: 302-304, 322-325.
Li Qi-hu. Sonar Signal Processing Introduction[M]. Second Edition, Beijing: Ocean Press, 2000: 302-304, 322-325.
[2] 张学森, 冯海泓, 黄敏燕, 等. 两步法提高时延差估计精度的分析和实验验证[J]. 声学学报, 2013, 38(2): 153-159.
Zhang Xue-sen, Feng Hai-hong, Huang Min-yan,.. Analysis and experimental verification on improving time-delay difference estimation accuracy with two-step algorithm[J]., 2013, 38(2): 153-159.
[3] 邢翠柳, 陈建民. 基于频率补偿的时延估计方法[J]. 飞行器测控学报, 2012, 3(1): 34-37.
Xing Cui-liu and Chen Jian-min. Method of delay estimation based on frequency compensation[J].&, 2012, 3(1): 34-37.
[4] 杨力, 钱博, 冯永新, 等. 提高BOC调制信号多相关峰值精度的三次样条播值法[J]. 系统实验学报, 2009, 21(12): 3573-3576.
Yang Li, Qian Bo, Feng Yong-xin,.. Improving BOC modulation signal multi-correlation peak measurement precision by cubic-spline interpolation[J]., 2009, 21(12): 3573-3576.
[5] 杨亦春, 马驰州, 李晓东, 等. 相关峰细化的精确时延估计快速算法研究[J]. 声学学报, 2003, 28(2): 159-166.
Yang Yi-chun, Ma Chi-zhou, Li Xiao-dong,.. Algorithm study of fast and accurate time-delay estimation with fine interpolation of correlation peak[J]., 2003, 28(2): 159-166.
[6] 郑琛瑶, 潘泉, 董真杰. 利用相关峰内插时延估计提高四元阵定位精度[J]. 声学技术, 2012, 31(5): 526-529.
Zheng Chen-yao, Pan Quan, and Dong Zhen-jie. Improvement of positioning precision of four-element-array by interpolating time-delay estimation in correlation peak[J]., 2012, 31(5): 526-529.
[7] 黄清. 相关域双谱时延估计方法[J]. 声学学报, 2003, 28(1): 57-60.
Huang Qing. Bispectrum time delay estimating based on correlation [J]., 2003, 28(1): 57-60.
[8] 李启虎, 李伟昌, 赵文立. 数字式声呐中的一种简化的ZoomFFT算法[J]. 声学学报, 2000, 25(2): 129-133.
Li Qi-hu, Li Wei-chang, and Zhao Wen-li. A simplified ZoomFFT algorithm in digital sonar[J]., 2000, 25(2): 129-133.
[9] 赵小燕, 汤捷, 周琳, 等. 基于相位差复指数变换的传声器多声源定位[J]. 东南大学学报(自然科学版), 2013, 43(2): 231-235.
Zhao Xiao-yan, Tang Jie, Zhou-lin,.. Multiple sound source localization of microphones based on complex exponential transform of phase differences[J].(), 2013, 43(2): 231-235.
[10] Ryo H, Masao Y, Tamaki U,.. Localization of sperm whales in a group using clicks received at two separated short baseline arrays[J]., 2010, 127(1): 133-147.
[11] Francesco N. Generalized state coherence transform for multidimensional TDOA estimation of multiple sources[J]., 2012, 20(1): 246-260.
[12] 马晓红, 陆晓燕, 殷福亮. 改进的互功率谱相位时延估计方法[J]. 电子与信息学报, 2004, 26(1): 53-59.
Ma Xiao-hong, Lu Xiao-yan, and Yin Fu-liang. Time delay estimation by using modified cross power spectrum phase technique[J].&, 2004, 26(1): 53-59.
[13] Piersol A. Time delay estimation using phase data[J]., 1981, 29(3): 471-477.
[14] Jonathan L O, Jeffrey L K, and Jeffrey S R. Maximum- likelihood spatial spectrum estimation in dynamic environment with a short maneuverable array[J]., 2013, 133(1): 311-322.
[15] Pasu P S and Alford W J. Range and bearing estimation in Passive sonar[J]., 1980, 16(2): 244-249.
[16] Schultheiss P M and Weistein E. Detection and estimation a summary of results[C]. Proceedings of the NATO Advanced Study Institute on Underwater Acoustics and Signal Processing, Copenhagen, Denmark, 1981: 379-410.
[17] Quazi A H. An overview on time delay estimate in active and passive system for target localization[J].,, 1981, 29(3): 527-533.
郑恩明: 男,1985年生,博士生,研究方向为水声信号与信息处理、水下声学定位系统.
丘 彦: 男,1981年生,工程师,研究方向为信号处理.
孙长瑜: 男,1954年生,研究员,博士生导师,主要研究方向为阵列信号处理.
陈新华: 男,1978年生,副研究员,主要研究方向为阵列信号处理.
Investigation on Time Delay Difference Estimation for Three-element Array Passive Positioning
Zheng En-ming①②Qiu Yan③Sun Chang-yu①Chen Xin-hua①
①(,,100190,)②(,100190,)③(91388,524022,)

Information processing technology; Passive positioning; Time delay difference estimation
TB565
A
1009-5896(2014)03-0639-06
10.3724/SP.J.1146.2013.00758
2013-05-27收到,2013-08-26改回
国家海洋公益性行业科研专项经费项目(201005001)资助课题
郑恩明 zhengenmingioa@163.com

