基于压缩感知的DOA估计稀疏化模型与性能分析

林 波 张增辉 朱炬波



基于压缩感知的DOA估计稀疏化模型与性能分析

林 波*张增辉 朱炬波

(国防科技大学理学院 长沙 410073)

利用压缩感知理论解决阵列信号到达角(DOA)估计问题，具有对快拍数据量要求低、可处理相关源等优点。将压缩感知理论应用于信源DOA估计的一个关键问题是建立信源信号的稀疏化模型。该文在均匀线阵模型下系统分析了角度划分对DOA估计稀疏重构性能的影响，从对相关性的分析出发给出了信号的最优稀疏化模型。分析结果表明在实际应用中基于信源信号等正弦空间稀疏化的重构模型是最优的。实验对比了新的稀疏化模型与传统的等角度划分方式得到的流形矩阵的可重构性能，并进行了关于信号重构和信源DOA估计的详细实验分析，验证了所提模型的优越性。

压缩感知(CS)；稀疏化模型；到达方向(DOA)估计；相关性

1 引言

阵列信号到达角(Direction-Of-Arrival, DOA)估计是阵列信号处理领域的关键问题，在雷达、通讯、地震等众多领域有广泛应用。空间谱估计技术的发展实现了目标DOA的超分辨估计。经典的空间谱估计算法包括MUSIC和ESPRIT算法，它们主要是根据阵列接收信号的统计特性来估计目标的到达角，因此需要大量独立同分布的测量数据。最新的压缩感知(Compressive Sensing, CS) 理论为DOA估计克服上述问题带来了新的技术途径。

将压缩感知理论应用于DOA估计问题，首先要建立合适的角度估计的稀疏表示和重构模型，空域稀疏化方式决定了模型的重构性能。然而到目前为止，利用压缩感知估计信号DOA的文献对稀疏化模型的建立都没有进行系统地理论阐述，通常都是简单地采用空域等角度稀疏化方式。本文分析了稀疏表示和重构模型对DOA估计性能的影响，并在此基础之上，从相关性条件的理论分析出发给出了信号的最优稀疏表示模型，并通过相关性条件的理论分析和仿真实验证实，提出了在实际应用中最优空间稀疏表示模型是等正弦空间稀疏表示模型，该模型比传统的等角度空间稀疏化得到的流形矩阵具有更加优越的稀疏重构性能。

2 基于压缩感知的阵列DOA估计模型

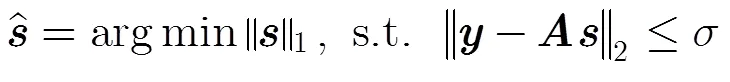
3 信源信号稀疏化模型与重构性能分析

3.1 稀疏重构条件与重构性能

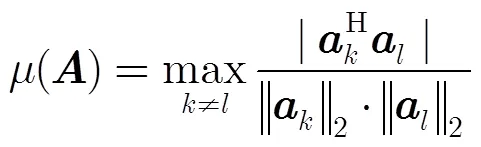
最近文献[15]从相关性条件出发给出了由式(2)所示优化问题稳健重构信号的条件和重构误差上界。

3.2 角度稀疏化模型

下面从阵列流形矩阵的相关性出发，构造阵列DOA估计的最优空域稀疏化模型。

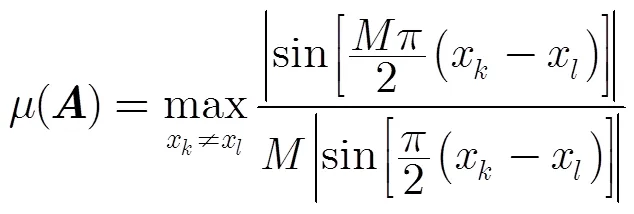
在区间[-1,1]中选取个点。下面分情况讨论该优化问题的最优解。

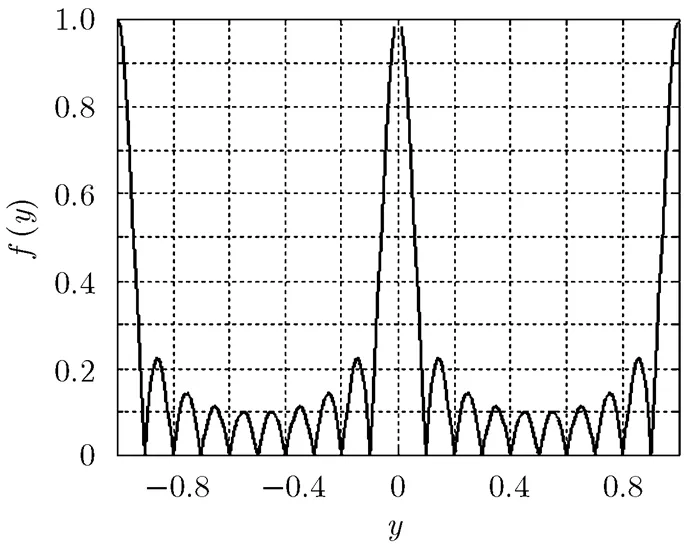
图2 M=10时的函数

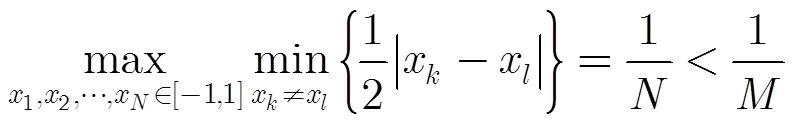
4 仿真实验及分析

以下用实验首先验证，利用本文方法获得的空域等正弦稀疏化模型对应的阵列流形矩阵的相关性比通常直接等角度划分的相关性小。

图3给出了当分别取10和20时，从10取到100的情况下，按照本文方法获得的阵列流形矩阵相关性与直接等角度划分结果的对比。由图3所示结果可以看出，通过空域稀疏化模型的优化处理，阵列流形矩阵的相关性得到了降低。

实验1 基于等正弦空间稀疏化的CS稀疏重构的DOA估计算法与MUSIC算法之间的DOA估计谱峰对比。

本实验针对个独立的远场窄带信源输入信号，对比基于等正弦空间稀疏化的CS稀疏重构算法与MUSIC算法的DOA估计性能。实验设置信噪比为SNR=10 dB，均匀线阵的阵元数为=40，全空间划分网格数为=201。为对比方便，将MUSIC算法的搜索点取在该网格上，使用快拍数为100。

图4给出了信源非相干时本文算法与MUSIC算法的DOA估计谱峰对比结果，图4(a)中两个信源的入射角分别为-8.1°和15.3°，图4(b)中两个信源的入射角分别为-0.1°和5.3°。实验结果表明，当两信源相距较近时，利用1个快拍数据的稀疏重构方法用于DOA估计时分辨率没有经典的MUSIC算法的分辨率高，然而由此实验可知基于压缩感知思想利用较少的快拍数处理阵列信号的DOA估计问题是一种可行的方案。

下面从信号恢复性能的角度说明本文方法的有效性。在实际的应用中，为了提高角度估计的精度，一般选取较大的，此时最优的空域稀疏化模型对应了等正弦的角度划分方式。下面的仿真试验主要对比等正弦角度划分和等角度划分的性能。

实验2 等正弦CS稀疏重构算法与等角度CS稀疏重构算法的信源信号重构性能对比。

实验3 等正弦CS稀疏重构算法与等角度CS稀疏重构算法的信源DOA估计性能对比。

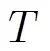
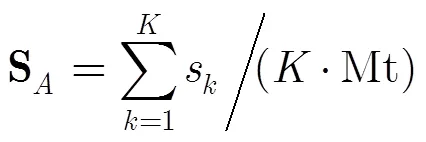
图7显示了不同信噪比下本文方法和等角度CS重构算法的DOA估计整体成功概率和累积成功概率，从图7所示结果可知，在此仿真实验中当信噪比低于13 dB时，本文方法的DOA估计整体成功概率和累积成功概率高于等角度CS重构算法。

5 结论

本文将压缩感知理论应用于阵列信号的DOA估计问题中，分析了信号的稀疏表示模型对信号稀疏恢复与信源DOA估计的影响，基于相关性条件的理论分析，给出了基于压缩感知解决DOA估计问题时最优的信号稀疏表示模型。为了便于数学分析，本文的理论分析是建立在均匀线阵的假设前提下，然而，压缩感知理论的稀疏重构思想应用于信源DOA估计的本质在于信源信号的空间稀疏性，针对不同的阵列构型和相应的数学模型同样可以应用稀疏重构的思想和方法。为了提高角度估计的精度，在DOA估计问题的实际应用中一般选取较大的空间稀疏化程度,大于，此时最优的空域稀疏化模型对应了等正弦稀疏化方式。数值实验对比也表明，等正弦信号空间稀疏化对应的阵列流形矩阵的相关性比传统的等角度信号空间稀疏化得到的阵列流形矩阵要小，具有更加显著的稀疏重构性能。

图3 本文提出的稀疏化模型获得的阵列流形矩阵相关性与等角度划分结果的对比

图5 等正弦CS稀疏重构与等角度CS稀疏重构算法的信源信号重构

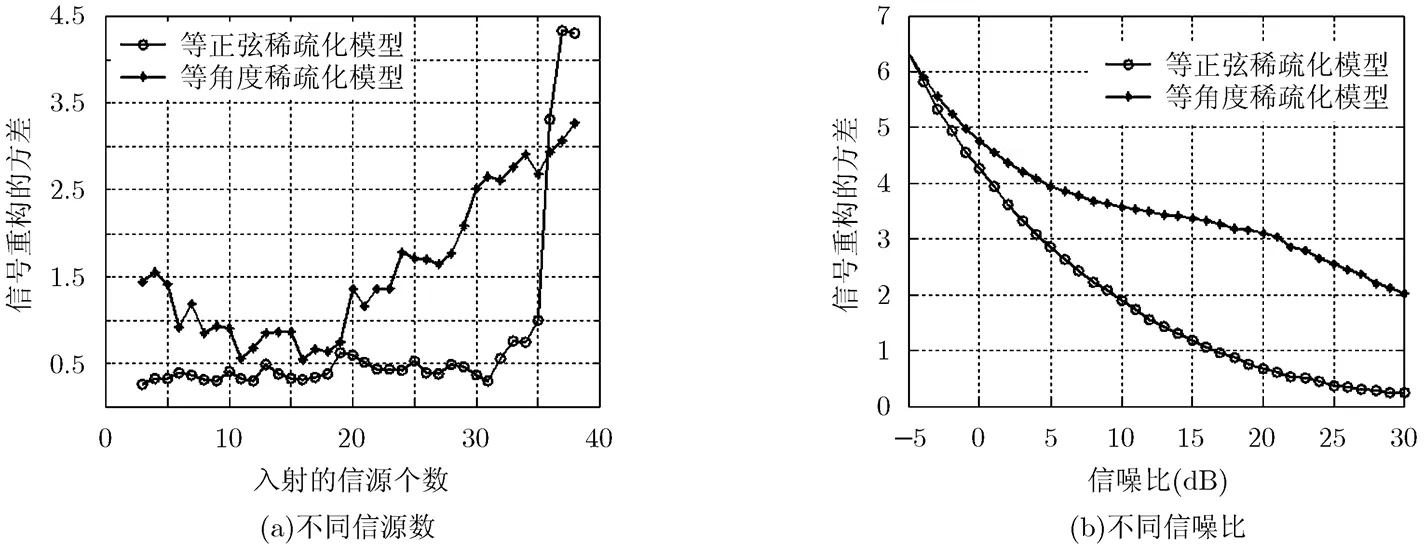
图6 信号重构的均方根误差

图7 不同信噪比下信源DOA估计的成功概率

仿真实验验证表明，基于本文提出的信号稀疏化表示和稀疏重构模型，利用压缩感知理论处理DOA估计问题是一种可行的新方法。当然，该方法受到压缩理论研究的局限性，如果仅利用稀疏重构的思想实现一步估计，目前在许多方面还无法突破经典的具有超分辨性能的MUSIC算法的性能。近几年已有不少研究利用多测量矢量模型、一般误差模型的压缩感知理论和网格细化处理等方法以进一步提高稀疏重构方法的超分辨性能，而设计具有最优性能的稀疏重构模型是进行上述研究的前提之一。本文正是提出了一种DOA估计问题中的最优信号稀疏重构模型并进行了仿真实验的验证。

[1] Donoho D. Compressed sensing[J]., 2006, 52(4): 1289-1306.

[2] Candès E and Tao T. Decoding by linear programming[J]., 2005, 51(12): 4203-4215.

[3] Malioutov D, Cetin M, and Willsky A. A sparse signal reconstruction perspective for source localization with sensor arrays[J]., 2005, 53(8): 3010-3022.

[4] Cevher V, Boufounos P, Baraniuk R,.. Near-optimal bayesian localization via incoherence and sparsity[C].Proceedings of the International Conference on Information Processing in Sensor Networks, San Francisco, 2009: 205-216.

[5] Duarte M. Localization and bearing estimation via structured sparsity models[C]. Proceedings of the IEEE

Statistical Signal Processing Workshop, Ann Arbor, 2012:

333-336.

[6] Kim J, Lee O, and Ye J. Compressive MUSIC: revisiting the link between compressive sensing and array signal processing [J]., 2012, 58(1): 278-301.

[7] Lee K, Bresler Y, and Junge M. Subspace methods for joint sparse recovery[J]., 2012, 58(6): 3616-3641.

[8] Donoho D, Elad M, and Temlyakov V. Stable recovery of sparse overcomplete representations in the presence of noise[J]., 2006, 52(1): 6-18.

[9] Chi Yue-jie, Scharf L, Pezeshki A,. Sensitivity to basis mismatch in compressed sensing[J]., 2011, 59(5): 2182-2195.

[10] Herman M and Strohmer T. General deviants: an analysis of perturbations in compressed sensing[J]., 2010, 4(2): 342-349.

[11] Yang Zai, Xie Li-hua, and Zhang Ci-shen. Off-grid direction of arrival estimation using sparse bayesian inference[J]., 2013, 61(1): 38-43.

[12] Liu Zhang-meng and Zhou Yi-yu. A unified framework and sparse bayesian perspective for direction-of-arrival estimation in the presence of array imperfections[J]., 2013, 61(15): 3786-3798.

[13] Cai T and Zhang An-ru. Sharp RIP bound for sparse signal and low-rank matrix recovery[J]., 2013, 35(1): 74-93.

[14] Xu Zong-ben, Chang Xiang-yu, Xu Feng-min,..1/2regularization: a thresholding representation theory and a fast solver[J].2012, 23(7): 1013-1027.

[15] Cai T, Wang Lie, and Xu Guang-wu. Stable recovery of sparse signals and an oracle inequality[J].2010, 56(7): 3516-3522.

林 波： 女，1985年生，博士生，研究方向为压缩感知、阵列信号处理.

张增辉： 男，1980年生，博士，讲师，研究方向为压缩感知、阵列信号处理、空时自适应信号处理.

朱炬波： 男，1967年生，博士，教授，博士生导师，研究方向为系统科学、雷达信号处理、图像处理与数学成像.

Sparsity Model and Performance Analysis of DOA Estimation with Compressive Sensing

Lin Bo Zhang Zeng-hui Zhu Ju-bo

(,,410073,)

The method of Direction-Of-Arrival (DOA) estimation of array signals based on Compressive Sensing (CS) theory has advantages such as fewer snapshots requirement and the capacity of dealing with the coherent sources. Exploiting the CS theory on DOA estimation, one of the key issues is to construct the sparsity model of source signals. This paper proposes the systemic analysis about how the way of space-partition affects the performance of DOA estimation, and presents a new optimal sparse reconstruction model based on space-partition with equal sine interval through the analysis about coherence. The theoretical result shows that the reconstruction model based on the manifold matrix with equal sine interval is the best model in the practical application. Finally the experiments compare the reconstruction performance of the manifold matrix with equal sine interval with that of the manifold matrix with equal angle interval. This paper provides the experiment results about the performance of signal reconstruction and DOA estimation, respectively. The advantage of the presented sparsity model is verified.

Compressive Sensing (CS); Sparsity model; Direction-Of-Arrival (DOA) estimation; Coherence

TN911.7

A

1009-5896(2014)03-0589-06

10.3724/SP.J.1146.2013.00149

2013-01-25收到，2013-11-22改回

国家自然科学基金(61002024, 61072142, 61102169, 61201332, 61205190, 61271437)和国防科学技术大学科研计划项目(JC11- 02-03)资助课题

林波 linbo@nudt.edu.cn