方位多通道SAR信号重建性能分析

马喜乐 孙造宇 董 臻 何 峰 梁甸农



方位多通道SAR信号重建性能分析

马喜乐*孙造宇 董 臻 何 峰 梁甸农

(国防科学技术大学电子科学与工程学院 长沙 410073)

方位多通道合成孔径雷达(SAR)图像质量受系统参数、阵列误差以及信号处理方法等多种因素的影响。该文针对方位多通道SAR的信号重建性能进行深入分析。首先对信号模型进行完善，引入了重建系数的概念，从而使得多通道SAR信号重建网络的设计具有更大的灵活性，继而在数字波束形成的框架下对一系列重建方法进行了介绍。其次，在得到重建误差功率谱的基础上，进一步给出信噪比与方位模糊比的解析表达式。最后，对各种算法的重建性能进行了定量评估与分析。仿真实验验证了理论分析的正确性。分析结果将为方位多通道SAR系统设计、信号处理以及图像质量预估提供有效支撑。

合成孔径雷达；方位多通道；信号重建；性能分析

1 引言

信号重建滤波器对多普勒主瓣信号进行重建的同时也对噪声和杂波的旁瓣模糊分量产生调制，而阵列误差在导致主瓣信号损失的同时还将进一步对旁瓣模糊分量进行调制。文献[3]利用旁瓣杂波与噪声放大系数对LS算法的重建性能进行评价，其不足之处在于并未对旁瓣杂波与加性噪声作区别性分析，同时也未考虑到处理带宽的影响。文献[4]基于观测矩阵求逆的方法对方位多通道SAR的信噪比与方位模糊比进行了分析，但未能充分考察信号处理方法对图像质量的影响。此外，文献[3]，文献[4]并未考虑由阵列误差以及重建算法自身特点所导致的主瓣杂波误差。

与方位多通道SAR图像质量直接相关的两项关键指标为信噪比(SNR)与方位模糊比(AASR)。本文首先对信号模型进行完善，提出了重建系数的概念，从而使得多通道SAR信号重建方法具有更大的可选择性，继而在DBF的框架下对一系列重建方法进行介绍；其次，推导了重建误差功率谱的解析表达式，在此基础上给出了信噪比与方位模糊比的解析表达式；最后，对各种重建算法的性能进行定量评估与分析。

2 方位谱重建方法

2.1 信号模型

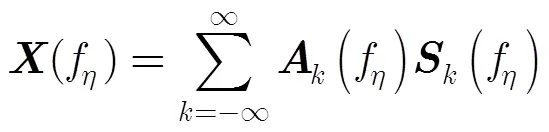
图1 方位多通道 SAR空间采样示意图

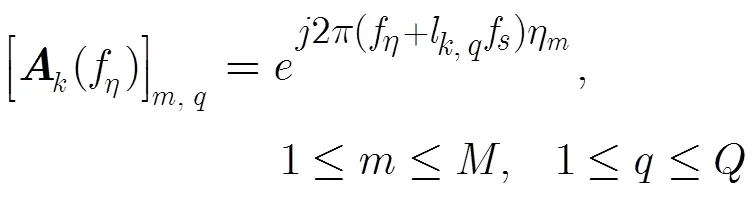
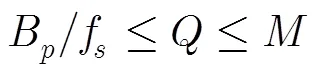
进一步考虑幅相误差以及接收噪声的影响，信号模型修正为

2.2 重建方法

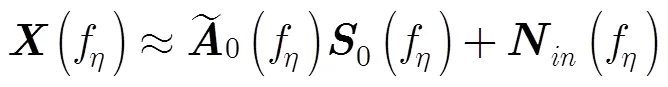
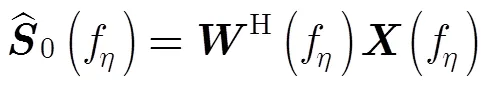
基于式(7)给出的近似信号模型，一系列经典的DBF方法[11, 12]可用于信号重建。鉴于相关方法在文献中均有详细论述，本文仅对以下几种DBF方法予以简单介绍：

(1)LS算法：根据式(7)的近似模型，进一步忽略噪声的影响，可以得到LS估计器[3, 11]：

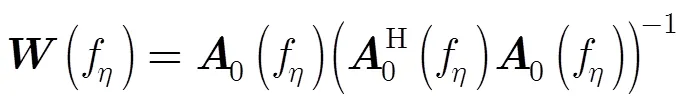
(2)Capon算法：线性约束最小功率(LCMP)波束形成器的核心思想是在某种线性约束条件下通过最小化阵列输出功率求得滤波器的权值[12]，而这一核心思想首先由Capon提出。为便于表述，本文将无畸变约束条件下的LCMP波束形成器称作单平面波Capon估计器，简记为Capon-S；而将零点约束条件下的LCMP波束形成器称作多平面波Capon估计器，简记为Capon-M。

Capon-S波束形成器为[2, 12]

Capon-M波束形成器为[12]

(3)ES算法：本文将基于Capon-S算法与Capon-M算法的子空间投影处理方法分别记做ES-S和ES-M算法。对数据协方差矩阵进行特征分解，可得

3 信号重建性能分析

3.1 重建误差功率谱

结合式(8)，方位多通道SAR的重建误差矢量为

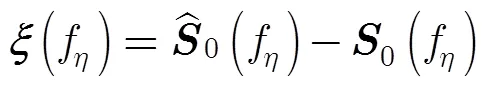
将式(5)，式(8)代入式(13)，得到

这样，误差功率谱可表示为

对于一般的地物场景，可以认为来自不同方向的杂波谱是不相关的，亦即

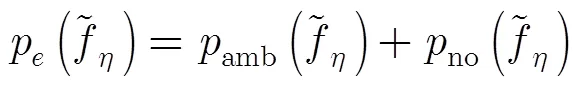
其中

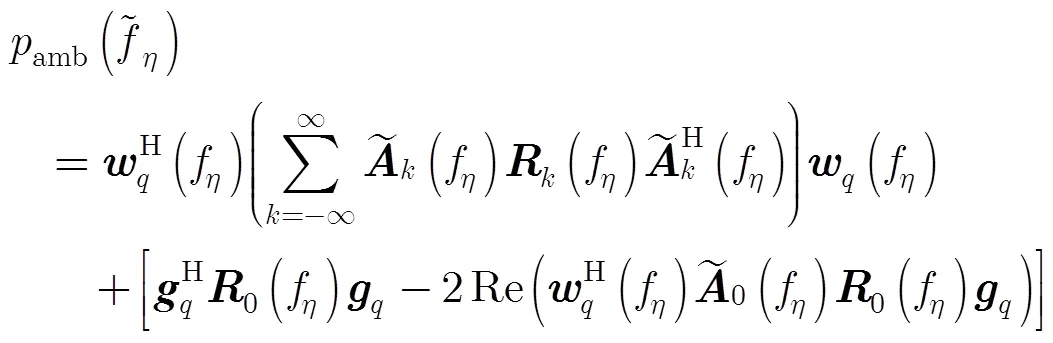
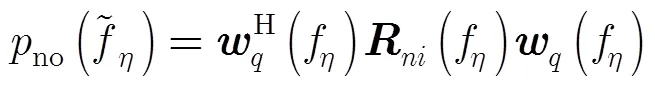
由式(5)，可以得到数据的协方差矩阵为

结合式(18)，式(19)与式(20)，重建误差功率谱简化为

3.2 信号重建性能指标

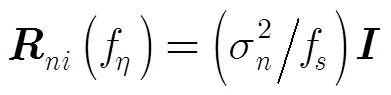
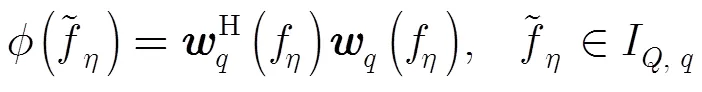
4 仿真分析

4.1 信号级仿真验证

输入信噪比设为5 dB，图4给出了信噪比调制系数与方位模糊比的理论值，仿真值以及二者的误差。由图4(c)可见，信噪比调制系数的仿真值与理论值取得了高度的吻合，最大误差不超过0.02 dB。由图4(f)可见，方位模糊比的仿真值与理论值同样取得了很好的吻合。对于LS与Capon-M算法，仿真值与理论值的最大误差不超过0.2 dB；对于Capon-S算法，最大误差小于0.7 dB。快时间样本的有限性以及与主瓣杂波的相关性会导致仿真值与理论值的偏差。由于LS与Capon-M算法能够对主瓣模糊进行更加充分的抑制，所以在这两种算法下的方位模糊比的仿真值与理论值可以取得更好的吻合。

4.2 性能分析与比较

表1 关键参数

图2 图像质量分析仿真流程图

图3 杂波仿真空间几何

图4 信号重建性能仿真验证

表2相位误差(o)

误差量级通道1通道2通道3通道4通道5通道6通道7 =00000000 =100-5.05.01.04.0-3.0-2.0

首先对低信噪比(SNRin=0 dB)条件下的信号重建性能进行分析。结合图5(a)，图5(b)，图5(c)与图5(d)，可以看到：(1)Capon-M与LS算法性能相当，而且随着PRF的升高，可通过值的调整在不损失方位模糊比的同时实现输出信噪比的优化。(2)Capon-S算法在输出信噪比方面优于Capon-M与LS算法，但是在方位模糊比方面存在显著的性能损失。(3)对Capon-M以及Capon-S算法来说，子空间投影处理并未有效实现重建性能的改善。

5 结束语

在综合考虑旁瓣杂波、加性噪声以及阵列误差等因素的情况下，本文对多通道SAR信号模型进行了完善。重建系数的提出大大增加了DBF方法的灵活性。本文推导了信号重建误差功率谱的解析表达式，以此为基础给出了输出信噪比与方位模糊比的解析表达式。信号级仿真验证了理论分析的正确性。方位多通道SAR图像质量受DBF方法，通道数，重建系数，输入信噪比，PRF，处理带宽B以及阵列误差等多种因素影响。通过对LS, Capon-S, Capon-M, ES-S以及ES-M等DBF方法的理论分析与比较，可以得到以下结论：(1)输入信噪比较低时，Capon-M与LS算法重建性能相当，而且随着PRF的升高，可以通过值的调整实现Capon-M与LS算法重建性能的提升。Capon-S算法则以方位模糊比为代价实现了输出信噪比的优化。(2)输入信噪比较高时，Capon-S方法对阵列误差最为敏感，但是子空间投影处理可以大大改善其对阵列误差的敏感度。当存在阵列误差时，通过值的调整以及子空间投影处理，Capon-M算法与LS算法取得较一致的重建性能并优于Capon-S算法。

图5 DBF网络对信号重建性能的影响

[1] Krieger G, Gebert N, and Moreira A. Unambiguous SAR signal reconstruction from nonuniform displaced phase center sampling[J]., 2004, 1(4): 260-264.

[2] Li Z, Bao Z, Wang H,Performance improvement for constellation SAR using signal processing techniques[J]., 2006, 42(2): 436-452.

[3] Wang T and Bao Z. Improving the image quality of spaceborne multiple-aperture SAR under minimization of sidelobe clutter and noise[J]., 2006, 3(3): 297-301.

[4] Gebert N, Krieger G, and Moreira A. Digital beamforming on receive-techniques and optimization strategies for high-resolution wide-swath SAR imaging[J]., 2009, 45(2): 564-590.

[5] Kou G , Wang Z, and Yao P. Multiple beams spaceborne SAR imaging[J]., 2012, 48(4): 3363-3375.

[6] Currie A and Brown M A. Wide-swath SAR[J]., 1992, 139(2): 122-135.

[7] Feng F, Li S, Yu W,.. Study on the processing scheme for space–time waveform encoding SAR system based on two-dimensional digital beamforming[J]., 2012, 50(3): 910-932.

[8] Morena L C, James K V, and Beck J. An introduction to the RADARSAT-2 mission[J]., 2004, 30(3): 221-234.

[9] Kim J H, Younis M, Prats P,.. Azimuth reconstruction demonstration using TerraSAR-X dual receive antenna mode [C]. International Geoscience and Romote Sensing Symposium, Munich, Germany, 2012: 1537-1540.

[10] Kim J H, Younis M, Prats P,.. First spaceborne demonstration of digital beamforming for azimuth ambiguity suppression[J]., 2013, 51(1): 579-589.

[11] Kay S M. Fundamentals of Statistical Signal Processing: Estimation Theory[M]. Upper Saddle River, New Jersey: Prentice-Hall, 1993, Ch. 8.

[12] Van Trees H L. Optimum Array Processing: Part IV of Detection, Estimation, and Modulation Theory[M]. New York: Wiley, 2002, Ch. 6.

[13] Yang T, Li Z, Liu Y,.. Channel error estimation methods for multichannel SAR systems in azimuth[J]., 2013, 10(3): 548-552.

[14] 刘艳阳, 李真芳, 杨桃丽, 等. 一种单星方位多通道高分辨率宽测绘带SAR系统通道相位偏差时域估计新方法[J]. 电子与信息学报, 2012, 34(12): 2913-2919.

Liu Yan-yang, Li Zhen-fang, Yan Tao-li.. A novel channel phase bias estimation method for spaceborne along-track multi-channel HRWS SAR in time-domain[J].&, 2012, 34(12): 2913-2919.

[15] Oppenheim A V, Schafer R W, and Buck J R. Discrete-Time Processing[M]. Upper Saddle River, New Jersey: Prentice-Hall, 1999, Ch. 8.

马喜乐： 男，1987年生，博士生，研究方向为高分辨宽测绘带SAR系统与信号处理.

孙造宇： 男，1978年生，讲师，研究方向为SAR、InSAR系统仿真及信号处理.

董 臻： 男，1973年生，研究员，研究方向为雷达系统与信号处理.

Signal Reconstruction Performance Analysis of Azimuth Multi-channel SAR

Ma Xi-le Sun Zao-yu Dong Zhen He Feng Liang Dian-nong

(,,410073,)

Image quality of azimuth multi-channel SAR is influenced by such factors as system parameters, array errors, and signal processing strategies. The image quality of azimuth multi-channel SAR is studied deeply. Firstly, the signal model is improved. The introduction of the reconstruction coefficient provides more flexibility for designing the reconstruction network. In the frame of digital beam-forming, a series of reconstruction algorithms are then discussed for signal reconstruction. Secondly, based on the power spectrum of the reconstruction error, the analytical expressions of output Signal to Noise Ratio (SNR) and Azimuth Ambiguity to Signal Ratio (AASR) are deduced. Thirdly, the performance of the reconstruction algorithms is assessed quantitatively. Simulation experiment results confirm the validity of the theoretical analysis. Theoretical results provide technique support to system design, signal processing and image quality evaluation of azimuth multi-channel SAR.

SAR; Azimuth multi-channel; Signal reconstruction; Performance analysis

TN957.51

A

1009-5896(2014)03-0545-07

10.3724/SP.J.1146.2013.00579

2013-04-25收到，2013-10-25改回

国家自然科学基金(61101187)资助课题

马喜乐 darkbone@126.com