多普勒频率变化率快速最大似然估计辅助的高动态载波跟踪环路

郇 浩 陶选如 陶 然 程小康 董 朝 李鹏飞



多普勒频率变化率快速最大似然估计辅助的高动态载波跟踪环路

郇 浩*陶选如 陶 然 程小康 董 朝 李鹏飞

(北京理工大学信息与电子学院 北京 100081)

高动态环境下接收信号含有较大的多普勒频率及其变化率，传统载波跟踪方法难以在高动态应力和跟踪精度两方面取得较好折中，针对这一问题该文提出一种多普勒频率变化率快速最大似然估计方法，并利用估计值辅助载波跟踪环路。首先指出了多普勒频率及其变化率的最大似然估计可等效采用分数阶傅里叶变换(FrFT)来实现；其次，针对频率及其变化率2维搜索运算量大的问题，提出一种瞬时自相关与分段离散傅里叶变换(DFT)求相位差相结合的频率变化率估计方法，根据粗估值可大大缩小搜索范围；最后，利用估计值辅助载波跟踪环路，降低动态应力，提高跟踪精度。理论分析与计算机仿真表明，在典型高动态参数条件下，输入信噪比为-30 dB时，搜索运算量降为原来的5.25%，输出频率的均方根误差仅为8.46 Hz/s，和传统载波跟踪方法相比，灵敏度提高3 dB以上。

载波跟踪；高动态；最大似然估计；瞬时自相关；离散傅里叶变换

1 引言

2 多普勒频率变化率的最大似然估计

接收信号的形式可以表示为

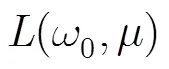
分数阶Fourier变换(Fractional Fourier Transform, FrFT)的积分定义为

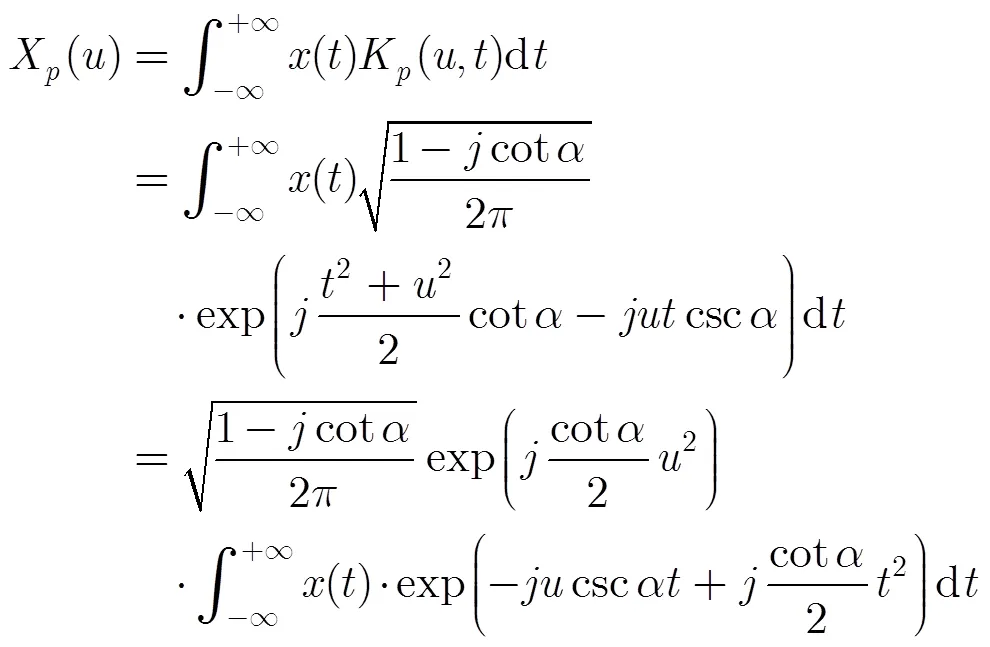
文献[12]指出，FrFT在检测未知的频率变化率时，调频率的搜索次数为

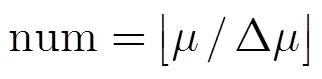
在参数未知的情况下，要得到两参数的最大似然估计，不得不采用全域搜索，同时为了得到较高的估计精度，又必须设置非常小的搜索步进，其搜索运算量非常大。假设频率变化率范围是-10~10 kHz/s，以10 Hz/s为搜索步进，至少需要2000次的搜索过程，每1次搜索都需要做1次FrFT进行最大值检测，这对于实时信号处理技术来说是难以接受的，下文就如何缩小调频率的搜索范围这一问题进行了详细研究。

3 基于多普勒频率变化率快速最大似然估计辅助的载波跟踪环路

针对搜索运算量大的问题，本文提出一种多普勒频率变化率快速估计方法，该方法不需要进行2维搜索，在高信噪比时估计性能接近Cramer-Rao下界，通过多普勒变化率的快速估计，能够大大缩小最大似然估计法的搜索范围，从而降低搜索运算量[13]。

3.1 瞬时自相关、分段DFT以及FRFT相结合的快速最大似然估计

首先，在利用瞬时自相关对信号进行降阶处理之前，为了提高输入信噪比，对信号进行分段相干积累，经过分段相干积累后的信号可表示为

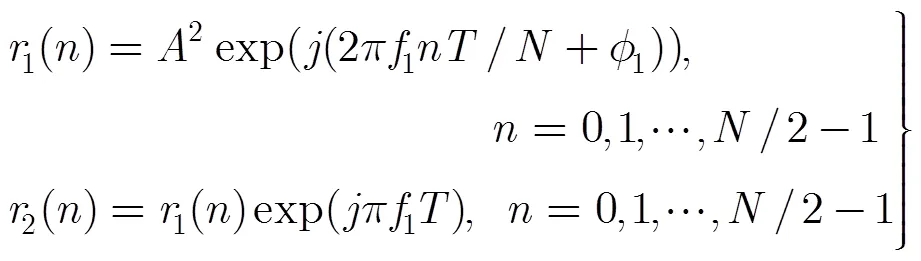
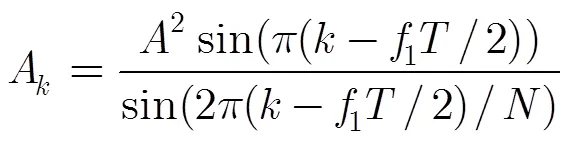
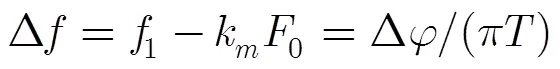
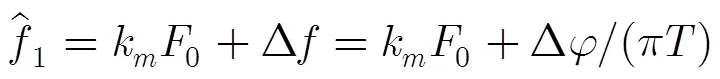
则信号的多普勒频率变化率的估计值为

从公式推导可以看出，经过一次相关运算及两次DFT即可实现多普勒频率变化率估计，而相关运算和DFT都可在数字信号处理芯片上快速计算，易于工程实现，通过增加信号的观测时间，可进一步提高估计精度。

图1所示为多普勒频率变化率快速最大似然估计的算法流程。

将以上的流程进行总结，算法的实现可分为以下几个步骤：

图1 多普勒频率变化率快速最大似然估计的算法流程图

3.2 算法性能分析

所以，瞬时自相关函数的输入信噪比可以表示为

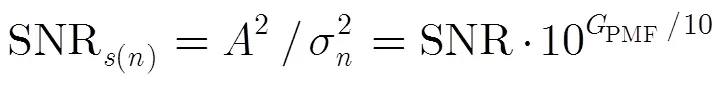
瞬时自相关函数输出为

瞬时自相关运算的输出信噪比可以表示为

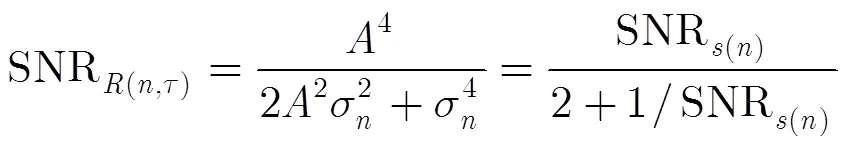
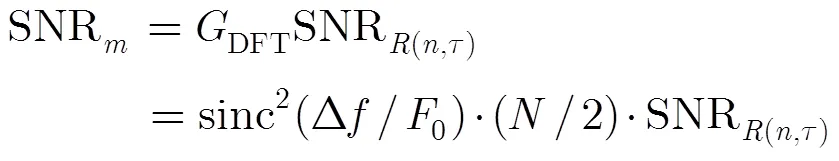
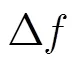
3.3基于多普勒频率变化率快速最大似然估计辅助的载波跟踪环路

参考INS与导航接收机深性耦合的原理，本文提出了一种多普勒频率变化率快速最大似然估计辅助的载波跟踪环路，通过得到多普勒变化率的估计值，将辅助信息接入载波环路，能够降低环路本身的动态应力，从而能够采用一个更窄的环路带宽来提高载波跟踪的灵敏度。并且这种数字信号处理的方法具有成本低、功耗小、没有时间积累误差的优点。

多普勒频率变化率快速最大似然估计辅助的载波跟踪环路原理框图如图2所示。

图2 多普勒频率变化率快速最大似然估计值辅助的载波跟踪原理框图

在环路动态较高时，采用多普勒频率变化率估计，将估计值反馈到载波数控振荡器(NCO)，载波NCO调整输出频率，使频率误差减小，相当于降低了跟踪环路的动态应力，锁频环承受的动态减弱，因此我们能够采用一个更窄的环路带宽来提高跟踪精度。

4 仿真结果及分析

4.1 多普勒频率变化率估计性能

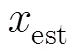
文献[16]给出了多普勒变化率估计的Cramer- Rao下界：

对本文提出的参数估计方法进行Monter Carlo仿真，并与Cramer-Rao下界对比，仿真结果如图4所示。

由图4能够看出，基于瞬时自相关降阶处理和DFT相位估计结合的多普勒变化率估计算法误差较大，但在输入信噪比大于-10 dB时，估计值的均方根误差接近CRLB；改进后的最大似然估计算法相比前者的估计精度明显提高，在输入信噪比为-27 dB时，估计值的均方根误差已经接近CRLB下限。通过本节提出的快速最大似然估计法，在低信噪比情况下能够提供精确的多普勒变化率估计值，此方法在保留传统最大似然估计较高跟踪精度的同时，不需要2维搜索，运算量相比传统的极大似然方法大大降低，因此该方法具有很好的工程应用前景。

4.2 辅助后跟踪环路性能

采用JPL定义的典型高动态模型，选取包含了-25的加速度和100/s的加加速度的过程。仿真过程中鉴频器的预检测积分时间为1 ms，最大似然估计器的观测时间为20 ms。

图5给出了3种高动态载波跟踪环路在SNR= -30 dB情况下的跟踪情况，图6对比了3种高动态载波跟踪环路的频率跟踪误差随信噪比的变化情况。

从图5和图6可以看出，在信噪比为-30 dB时，基于Kalman滤波的载波环路跟踪误差最大，基于FLL辅助PLL次之，而本文提出的基于多普勒频率变化率快速最大似然估计的载波环路跟踪误差最小，在信噪比为-30 dB时输出频率均方根误差仅为8.46 Hz/s，与FLL直接辅助PLL相比，跟踪灵敏度提高了3 dB以上。

图3 仿真值与理论值的对比

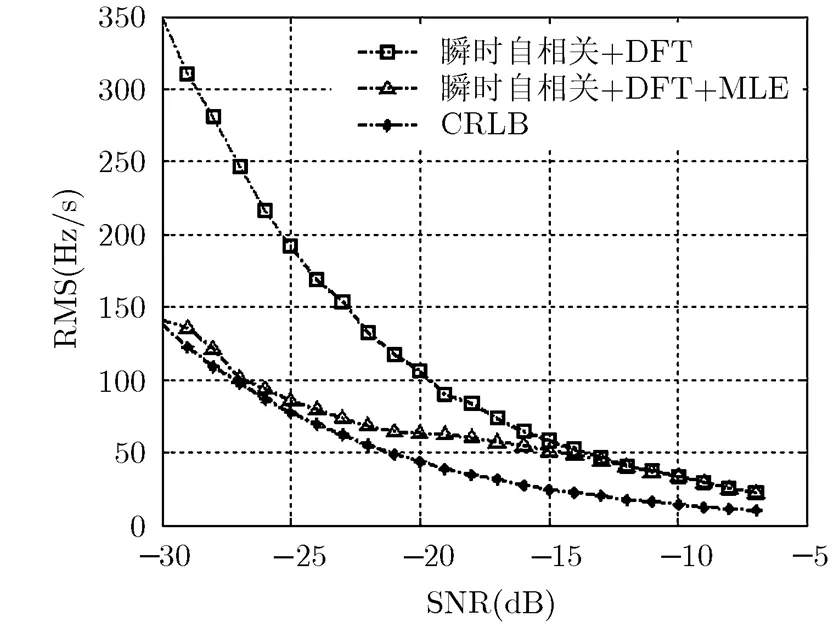
图4 算法的估计性能比较

图5 3种高动态载波跟踪效果对比

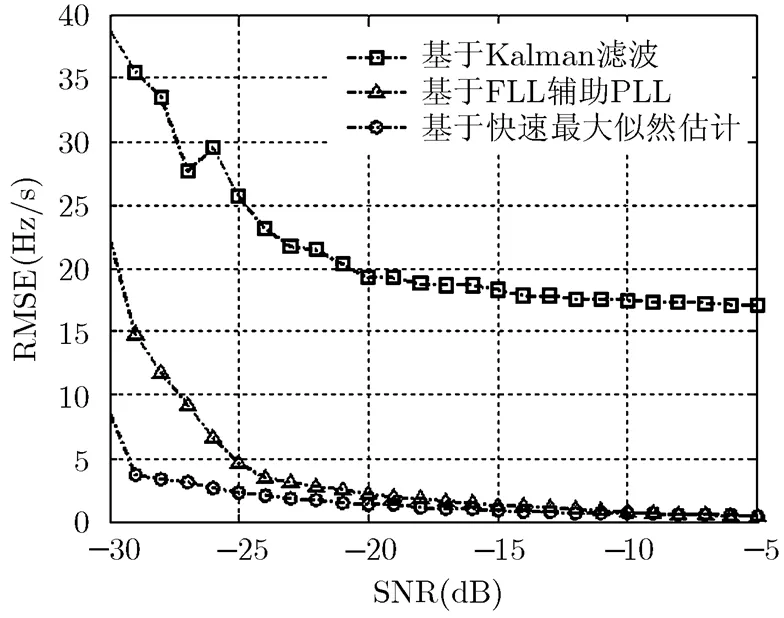
图6 3种高动态载波跟踪环路的性能对比

5 结束语

本文在研究传统最大似然估计方法的基础上，提出了基于多普勒频率变化率最大似然估计辅助的载波跟踪方法，多普勒频率变化率估计不需要2维搜索，运算量小，得到参数的粗略估计值后能够缩小最大似然估计的搜索范围，在输入信噪比为-30 dB时，搜索运算量减少为原来的5.25%。在典型高动态参数条件下，采用多普勒估计值辅助的载波跟踪环路，输入信噪比为-30 dB时，输出频率的均方根误差为8.46 Hz/s，与典型高动态载波跟踪环路方法相比，本文方法跟踪性能明显优于其它环路，灵敏度提高约3 dB以上，从而证明本文方法能很好地进行高动态扩频信号载波的跟踪，在保持最大似然估计较高跟踪精度的同时减小了运算量，该方法在导弹、深空测控、导航等遥测和通信领域具有较好的应用前景。

[1] 左启耀. 高动态GPS 信号跟踪算法研究[D]. [博士论文], 中国科学院研究生院(空间科学与应用研究中心), 2008.

[2] 田甜. 高动态环境下直扩通信同步技术研究[D]. [博士论文], 北京理工大学, 2012.

[3] Kamel M, Borio D, Nielsen J,.. Interference mitigation for highly dynamic GPS receivers using intelligent tracking loops[C]. The Institute of Navigatin GNSS, San Diego, 2011: 374-383.

[4] LianP, LachapelleG, and MaCL. Improving tracking performance of PLL in high dynamic applications[C]. The Institute of Navigatin NTM, San Diego, 2005: 24-26.

[5] 潘伟萍. 高动态直扩信号跟踪算法研究[D]. [硕士论文], 北京理工大学, 2011.

[6] Miao Jian-feng, Chen Wu, Sun Yong-rong,.. Adaptively robust phase lock loop for low C/N carrier tracking in a GPS software receiver[J]., 2011, 37(1): 52-60.

[7] Ward P W. Performance comparisons between FLL, PLL and a novel FLL-assisted-PLL carrier tracking loop under RF interference conditions[C]. Proceedings of the 11th International Technical Meeting of The Satellite Division of The Institute of Navigation, Nashville, 1998: 783-795.

[8] 邓晓东, 孙武. 基于FLL+PLL的载波跟踪环路设计[J]. 现代防御技术, 2010, 38(4): 137-141.

Deng Xiao-dong, Sun Wu. Design of carrier tracking loop based on FLL+PLL[J]., 2010, 38(4): 137-141.

[9] 刘苑伊, 赵昀, 耿生群, 等. 基于INS辅助的高动态GPS接收机算法研究[J]. 计算机工程与设计, 2011, 32(3): 1096-1098.

Liu Yuan-yi, Zhao Yun, Geng Sheng-qun,.. Research on INS aided high dynamic GPS receiver algorithm[J]., 2011, 32(3): 1096-1098.

[10] 周良臣, 杨建宇, 唐斌. 一种高效的LFM信号参数估计方法及性能分析[J]. 电子学报, 2007, 35(6): 1128-1133.

Zhou Liang-chen, Yang Jian-yu, Tang Bin. An efficient parameter estimation and performance analysis for LFM signal[J]., 2007, 35(6): 1128-1133.

[11] Bello P. Joint estimation of delay, Doppler, and Doppler rate[J]., 1960, 6(3): 330-341.

[12] Tao R, Zhang N, and Wang Y. Analyzing and compensating the effects of range and Doppler frequency migrations in linear frequency modulation pulse compressionradar[J].,&, 2011, 5(1): 12-22.

[13] 许剑锋, 王国华.线性调频信号参数的最大似然估计改进算法[C].全国第二届嵌入式技术联合学术会议论文集, 成都, 2007: 63-65.

[14] 齐国清. 基于DFT相位的正弦波频率和初相的高精度估计方法[J]. 电子学报, 2001, 29(9): 1164-1167.

Qi Guo-qing. High-accuracy frequency and phase estimation of single-tone based on phase of DFT[J]., 2001, 29(9): 1164-1167.

[15] 谢钢. GPS原理与接收机设计[M]. 北京: 电子工业出版社, 2009: 350-351.

[16] 王晓湘. 高动态多普勒频率估计及其Cramer-Rao界[J]. 电子与信息学报, 2004, 26(2): 206-212.

Wang Xiao-xiang. Estimation of high dynamic Doppler frequency and its Cramer-Rao bounds[J].&, 2004, 26(2): 206-212.

郇 浩： 男，1983年生，讲师，研究方向为分数阶傅里叶变换及其在雷达信号处理中的应用.

陶选如： 女，1989年生，硕士生，研究方向为高动态直扩信号同步技术.

陶 然： 男，1964年生，教授，研究方向为多活性代理信息系统以及先进信号处理.

Carrier Tracking Loop in High Dynamic Environment Aided by Fast Maximum Likelihood Estimation of Doppler Frequency Rate-of-change

Huan Hao Tao Xuan-ru Tao Ran Cheng Xiao-kang Dong Zhao Li Peng-fei

(,,100081,)

To reach a compromise between efficient dynamic performance and high tracking accuracy of carrier tracking loop in high-dynamic circumstance which results in large Doppler frequency and Doppler frequency rate-of-change, a fast maximum likelihood estimation method of Doppler frequency rate-of-change is proposed in this paper, and the estimation value is utilized to aid the carrier tracking loop. First, it is pointed out that the maximum likelihood estimation method of Doppler frequency and Doppler frequency rate-of-change is equivalent to the Fractional Fourier Fransform (FrFT). Second, the estimation method of Doppler frequency rate-of- change, which combines the instant self-correlation and the segmental Discrete Fourier Transform (DFT) is proposed to solve the large two-dimensional search calculation amount of the Doppler frequency and Doppler frequency rate-of-change, and the received coarse estimation value is applied to narrow down the search range. Finally, the estimation value is used in the carrier tracking loop to reduce the dynamic stress and improve the tracking accuracy. Theoretical analysis and computer simulation show that the search calculation amount falls to 5.25 percent of the original amount with Signal to Noise Ratio (SNR) -30 dB, and the Root Mean Sguare Error(RMSE) of frequency tracked is only 8.46 Hz/s, compared with the traditional carrier tracking method the tracking sensitivity can be improved more than 3 dB.

Carrier tracking; High dynamic; Maximum likelihood estimation; Instant self-correlation; Discrete Foureier Transform (DFT)

TN911.23

A

1009-5896(2014)03-0577-06

10.3724/SP.J.1146.2013.00638

2013-05-09收到，2013-11-08改回

教育部博士点基金(20121101130001), CAST重点基金(201215)和北京市自然科学基金(4112051)资助课题

郇浩 huanhao@bit.edu.cn