斜梁桥受力性能分析

杜岳涛，高晨珂

(1.长安大学公路学院，陕西 西安 710064; 2.西安思源学院，陕西 西安 710038)

0 引言

自上个世纪80年代，斜桥的建设进入高潮，公路城市建设部门改变了过去桥梁服从路线的思维模式，使得斜弯结构的桥梁在构造物中的比重越来越大，并且主要应用于对线型要求较高的高速公路及城市立体交通等。

由检索资料显示，最初斜梁桥的分析方法主要是解析法和正交桥理论的修正法，对象多是关于荷载横向分布的研究，主要以修正的正桥荷载横向分布计算方法为主。横向分布系数的概念对正桥是简单易懂且较精确的，但是根据国内外研究发现，斜梁桥的受力和正桥相比有很大不同，荷载作用在斜梁桥上时，不仅会产生弯矩，而且会产生扭矩，即所谓弯扭耦合，弯扭耦合的直接后果是跨中弯矩减小，横梁的弯矩增大，沿用横向分布系数的概念计算斜桥已不再适用，随着计算机和桥梁专业计算软件的发展，越来越多的桥梁工作者运用数值模拟法分析斜梁桥。

1 影响斜梁桥受力的因素

影响斜梁桥受力的因素有斜交角、弯扭刚度比、支承形式和宽跨比。

1.1 斜交角φ

斜交角有两种表示方法:一是桥梁轴线与支承边垂线的夹角φ;二是桥梁轴线与支承线的夹角。前者越大表示斜交程度越大，后者则是越小表示斜交程度越大。本文中所称斜交角指第1 种表示方法。斜交角是影响斜梁桥受力性能的主要因素，斜交角越小，斜梁桥受力特点越接近于正梁桥;斜交角越大，斜梁桥的弯扭耦合现象越明显。

1.2 弯扭刚度比k

k 为抗弯刚度EI 与抗扭刚度 GJ 之比，k 越小，跨中弯矩折减越大。主梁数增加，k 对多梁式斜梁桥受力影响增大。弯扭刚度比k 对箱形斜梁桥影响比肋梁式斜梁桥大。

1.3 支承形式

支承个数的多少、支承形式的变化，包括横桥向是否可以转动或者移动、是否采用弹性支承，对斜桥的内力分布有着显著的影响。

1.4 宽跨比b/l

宽跨比越大，桥面板相对宽度越大，斜桥的特点越明显，宽跨比较小的斜梁桥，受力行为接近于正桥，只是在支承线附近断面才显示出斜桥的特性。

本文主要研究以斜交角和宽跨比为参数的斜梁桥受力特性。

2 斜梁桥基本资料

以《预应力混凝土公路桥梁通用设计图成套技术—通用图设计计算书》中30 m 装配式预应力混凝土简支T 梁标准图(下称标准图)为基础进行数值分析。

桥梁标准跨径30 m，混凝土预制T 梁采用C50混凝土、现浇铺装层C40 混凝土、护栏C30 混凝土，预应力钢绞线采用φs15.2 mm，fpk=1 860 MPa，Ep=1.95 ×105MPa，普通钢筋采用 HRB335，fsk=335 MPa，Es=2.0 ×105MPa，为全预应力混凝土结构，以分离式路基宽24.5 m(高速公路)为例，图1和图2为桥梁横断面和立面构造。

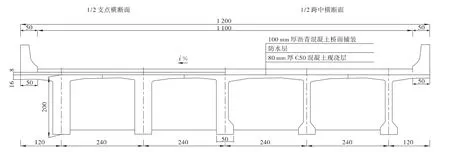
图1 横断面构造(单位:cm)

图2 立面构造(单位:cm)

T 梁截面构造如图3和图4所示。

图3 跨中截面(单位:cm)

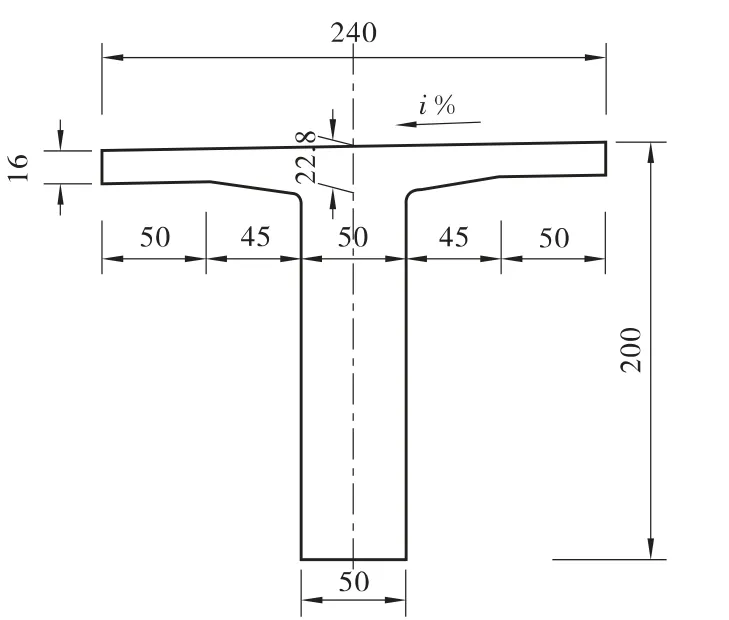
图4 支座截面(单位:cm)

3 斜梁桥参数模型分析

3.1 有限元模型

本文借助有限元分析软件MIDAS/Civil 进行斜梁桥的恒载内力计算，根据截面尺寸及材料建立斜梁桥有限元模型。对于预制拼装的T 形截面梁，常用梁格法建模，梁格法的主要思路是将桥跨结构用一个等效的梁网格来简化，将分散在梁每个区域内弯曲刚度和抗扭刚度“凝聚”于最邻近的等效梁格内，即将实际结构的纵向刚度“凝聚”于纵向梁格内，而横向刚度则“凝聚”于横向梁格内。

以斜交角为30°、宽跨比0.4 的5 片T 梁斜梁桥为例，全桥共划分265 个节点、380 个单元。为研究纵梁力学特性，每片纵梁为36 个梁单元、37 个节点。

整孔结构的边界条件在有限元分析中模拟如下:每片梁下用一般支承模拟支座受力，所有支座中只有一个支座约束Dx、Dy、Dz，其余支座只约束Dz，并通过弹性连接中的刚性来模拟T 梁顶部和底部的连接。有限元模型如图5所示。

模型中荷载考虑自重、二期恒载、预应力荷载及挂车－120 荷载。二期恒载为14.45 kN/m;根据标准图提供的预应力钢束，边梁采用3 束11φs15.2 钢绞线，中梁采用 1 束 11φs15.2 和 2 束 10φs15.2 钢绞线，钢束形状详见标准图。挂车－120 按《公路桥梁设计通用规范JTJ 021－89》加载，建模时将挂车－120以节点荷载的形式加载于纵桥向和横桥向中心位置。

本文着重研究挂车－120 荷载作用下边梁的弯矩变化情况，选取图5中最外侧的边梁进行研究，左支座为锐角处支座，右支座为钝角处支座，模型分别选取斜交角为 0°、30°、45°、60°，选取 3 片、5 片、7片、9 片T 梁进行受力分析，相应的宽跨比分别为0.24、0.4、0.56、0.72。

图5 斜梁桥有限元模型

3.2 斜交角为0°时

斜交角为0°时为正桥，图6所示为斜交角φ =0°时不同宽跨比边梁弯矩分布。

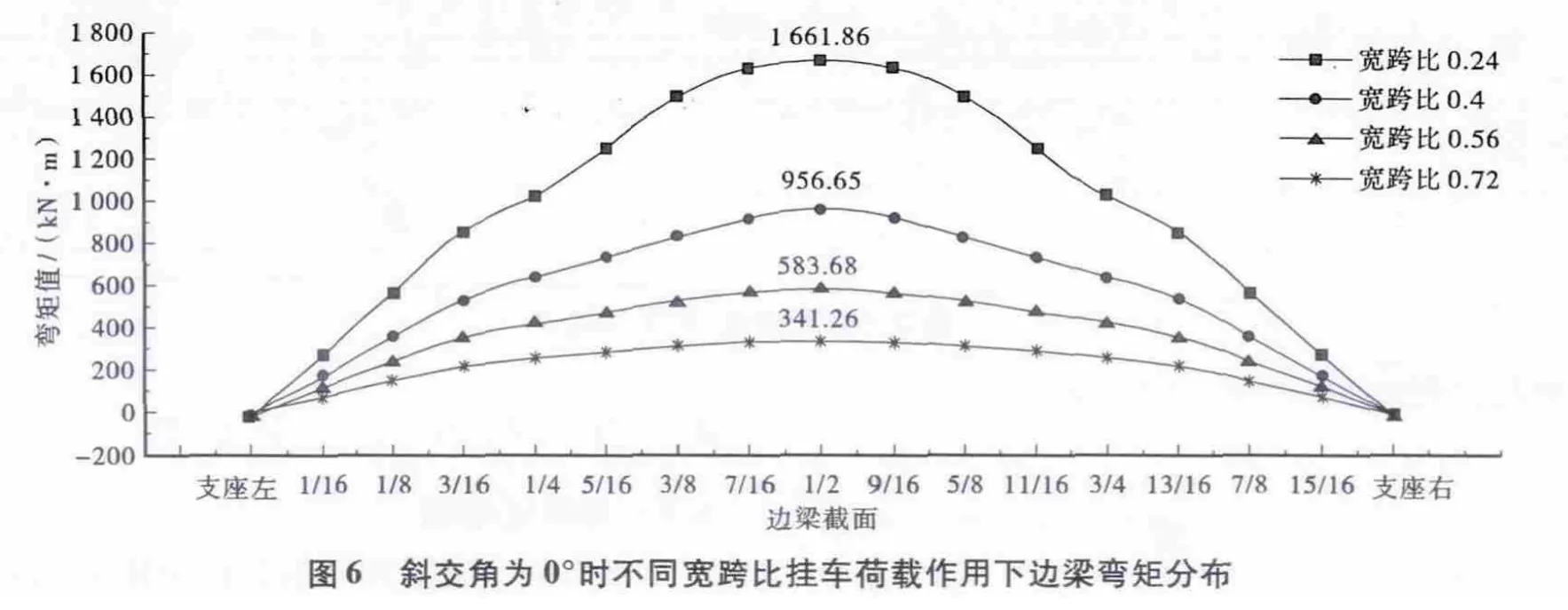
由图6可以看出，不同宽跨比在挂车－120 荷载作用下的边梁弯矩均关于跨中截面对称，符合正桥受力特征。由于挂车－120 荷载作用在横桥向的中心位置，随着宽跨比增大，边梁最大弯矩值减小。

3.3 斜交角为30°时

图7所示为斜交角φ =30°时不同宽跨比边梁弯矩分布图。

由图7可以看出，斜交角φ=30°时在挂车－120荷载作用下的边梁弯矩图关于1/2 截面大体也是对称的，由于挂车－120 荷载作用在横桥向的中心位置，随着宽跨比增大，边梁最大弯矩值减小。最大弯矩均出现在1/2 截面处，左支座处为锐角处，存在负弯矩，右支座为钝角处，由于横隔板的影响整体受力，正负弯矩均会出现。

3.4 斜交角为45°时

图8所示为斜交角φ =45°时不同宽跨比边梁弯矩分布图。

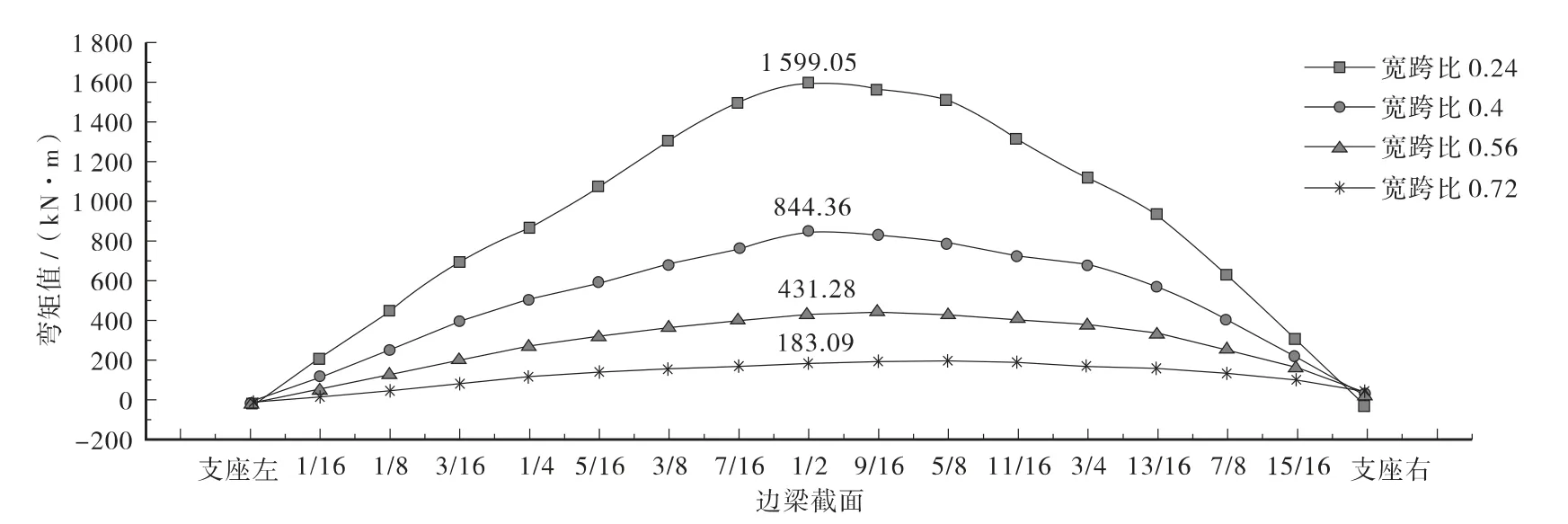
图8 斜交角φ=45°时不同宽跨比挂车荷载作用下边梁弯矩分布

由图8可以看出，由于挂车－120 荷载作用在横桥向的中心位置，随着宽跨比增大，边梁最大弯矩值减小，斜交角φ =45°时在挂车－120 荷载作用下不同宽跨比的边梁弯矩图均出现跨中截面右侧弯矩较左侧大的情况，即较大值向钝角方向偏移的情况。最大弯矩出现在1/2 截面处，左支座处为锐角处，存在负弯矩，右支座为钝角处，由于横隔板的影响整体受力，正负弯矩均会出现。

3.5 斜交角为60°时

图9所示为斜交角φ =60°时不同宽跨比边梁弯矩分布图。

图9 斜交角φ=60°时不同宽跨比挂车荷载作用下边梁弯矩分布

由图9可以看出，由于挂车－120 荷载作用在横桥向的中心位置，随着宽跨比增大，边梁最大弯矩值减小，斜交角φ =60°时在挂车－120 荷载作用下不同宽跨比的边梁弯矩图均出现跨中截面右侧弯矩较左侧大的情况，即较大值向钝角方向偏移的情况与斜交角φ=45°偏移量相比，斜交角φ=60°弯矩偏移量更大。斜交角φ =60°、3 片梁(宽跨比0.24)时，最大值出现在跨中位置;5 片梁(宽跨比0.4)最大值出现在跨中位置;7 片梁和9 片梁(宽跨比0.72)时已经很明显地出现边梁弯矩峰值向钝角方向偏移。左支座处为锐角处，存在负弯矩，右支座为钝角处，由于横隔板的影响整体受力，正负弯矩均会出现。

4 结果分析

将斜交角 φ 为 30°、45°、60°时在挂车－120 荷载作用下的边梁跨中弯矩相对斜交角φ 为0°时边梁跨中弯矩减小百分比的结果汇总，得到表1及图10。

表1 斜梁桥边梁跨中相对正梁桥边梁跨中弯矩减小百分比

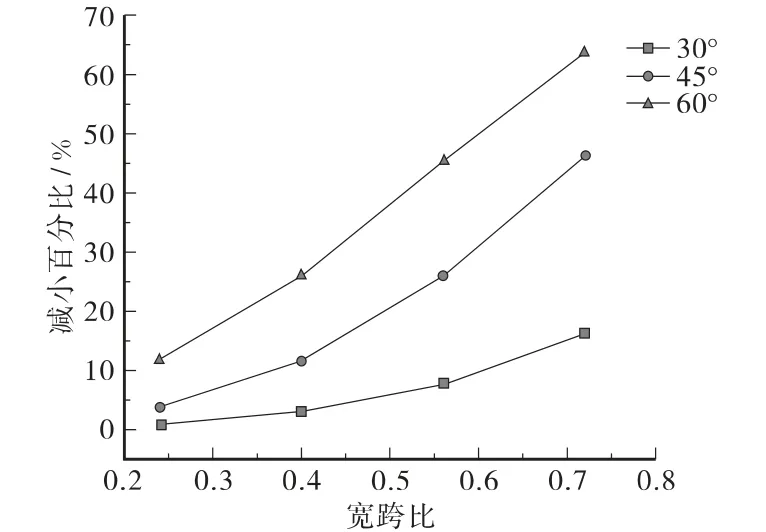
图10 斜梁桥边梁跨中相对正梁桥跨中弯矩减小百分比曲线

由表1和图10可以看出，与斜交角0°的正桥相比，斜梁桥在同一角度下，随着宽跨比的增加，边梁的弯矩减小百分比增大，斜交角为30°时的增大幅度不大，45°次之，60°最大;与斜交角0°的正桥相比，斜梁桥在同一宽跨比下，随着角度的增加，边梁的弯矩减小百分比增大，斜交角为30°时的增大幅度不大，45°次之，60°最大。

5 结论

由本文分析可以看出，随着斜交角和宽跨比的增大，斜梁桥的受力特性从类似正桥的受力特性逐渐变化，弯矩峰值向钝角方向靠拢，这种现象对边梁尤其明显，对中梁来说，越靠近桥梁纵向中心线的梁受力越接近正桥。因此在进行斜梁桥设计及加固时应当考虑斜梁桥的受力特性，制定相应的设计或加固方案。

［1］黄平明.混凝土斜梁桥［M］.北京:人民交通出版社，1995.

［2］徐 涛，吕福钢，万其柏.斜桥计算分析的发展［J］.辽宁交通科技，2005(7):71 －73.

［3］黄平明.斜梁桥横向刚度研究［J］.中国公路学报，1998，11(4):58 －63.

［4］黄平明.斜梁桥模型试验研究［J］.西安公路交通大学学报，1999，19(1):41 －47.

［5］曾 丽.斜梁桥的组合有限单元方法计算分析研究［D］.成都:西南交通大学，2001.

［6］刘菊玖.对斜梁桥荷载横向分布部分特点的探讨［J］.市政技术，2002(3):42 －45.

［7］徐晓龙，杨骊先，孙炳楠.斜交预应力混凝土板梁桥的计算模型与试验研究［J］.中国市政工程，2006(5):28 －30.

［8］杨 韬.简支转连续斜梁桥静力性能分析［D］.哈尔滨:哈尔滨工业大学，2007.

［9］史 梁，王积鑫，耿 鑫.考虑结构长期性能多梁式预应力混凝土斜梁桥合理施工方法研究［J］.北方交通，2008(6):138 －140.