集装箱自装卸运输车工作装置铰点位置对油缸载荷影响
成 凯,高 健,程 磊
(1.吉林大学 机械科学与工程学院,吉林 长春 130025;2.徐州徐工随车起重机有限公司,江苏 徐州 221000)
随着我国物流业的迅猛发展,门对门运输需求也逐步增加.我国现阶段应用最多的仍是效率较低、方法单一的装卸模式:集装箱运输车辆到达装卸货地点后,再租用集装箱起重机或正面吊进行装卸.集装箱侧面自装卸运输车是将装卸与运输结合在一起的车辆,工作效率高[1].
对集装箱侧面自装卸运输车(简称侧面吊,下同)的开发设计得到了各大企业的重视[2-3].在设计初期,工作装置铰点位置大多数时候都是通过“经验+试验”确定,需要大量人力、物力,研制周期长.基于此,本文从实际设计角度出发,结合侧面吊的实际作业工况,对侧面吊工作装置的铰点位置进行理论研究,并运用动力学仿真分析软件ADAMS进行对比试验,最终得出铰点位置对油缸载荷、工作幅度等的影响规律.图1所示为侧面吊工作状态.
1 铰点位置对油缸载荷影响的数学模型分析
1.1 数学模型
将侧面吊工作装置简化为平面动力学系统[2-5],包括上吊臂部分(包括上吊臂和上臂油缸)、下吊臂部分(包括下吊臂和下臂油缸)和支座部分等.工作机构由油缸驱动,并且以下臂油缸载荷作为主要研究目标.坐标系设定如下:横轴为x,纵轴为y,坐标系原点为车架中心线与地面的交点.
图2中各铰点意义:A为下臂油缸下铰点,B为下吊臂下铰点,C为上臂油缸下铰点,D为下臂油缸上铰点,E为上臂油缸上铰点,F为上吊臂上铰点,G为上吊臂下铰点.

图1 侧面吊工作状态图Fig.1 Working position of side container crane

图2 侧面吊工作装置油缸全收状态及边界Fig.2 Contraction state and boundary of side container crane’cylinders
假设侧面吊工作装置在工作过程中某一时刻状态如图3所示,将侧面吊工作装置按下吊臂部分和上吊臂部分进行分解,将上吊臂部分看作一个整体,建立下吊臂分离体的力学平衡方程[5].
下吊臂部分B点的矩平衡方程为

其中,

对式(1)进行整理,得

作业幅度方程为
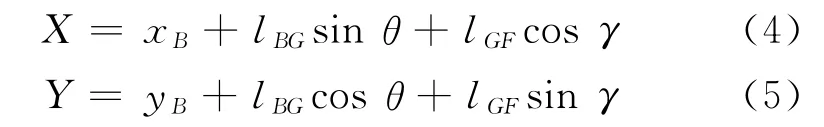
将式(2)代入式(5),得

式中:P1为下臂油缸载荷;lBD,lBG,lGF分别为铰点BD,BG,GF之间的距离;α为直线AD与直线BD所夹锐角;S为工作装置的起重力;a为铰点B与铰点F之间的水平距离;X为作业幅度中的远度,同时也是作业过程中铰点F的动态横坐标;xB为铰点B的横坐标;Y为作业幅度中的高度,同时也是作业过程中铰点F的动态纵坐标;yB为铰点B的纵坐标;θ为直线BG与纵轴所夹锐角;γ为直线GF与横轴所夹锐角.

图3 侧面吊工作装置任意工作位置Fig.3 Optional position of side container crane
1.2 各铰点位置与油缸载荷的关系
由式(3)可以看出,影响下臂油缸载荷的因素为:S,a,lBD和α.由于起重力S与铰点位置无关,在这里不予研究.下面分析各铰点通过a,lBD,α三个因素对油缸载荷P1的影响.
(1)P1随a的减小而减小.影响a的铰点有B,G,F三个铰点.因为有作业幅度的要求,假定远度不变,即式(4)中X不变.由式(6)可知,xB越大,a越小,即铰点B向右侧移动,会使下臂油缸载荷减小.
(2)lBD越大P1越小.铰点D向远离B点的方向移动,对下臂油缸载荷的影响有利.
(3)sinα越大P1越小,即α越大P1越小.当工作幅度X,Y不变时,影响α的铰点有A,B,D三个铰点.如图4所示,A点向左上移动,α变大;如图5所示B点向右下移动,α变大;如图6所示D点向上运动,α变大.由此可知,铰点A向左侧和上侧移动,铰点B向右侧和下侧移动,铰点D向远离B点的方向移动,都会使下臂油缸载荷减小,对下臂油缸载荷的影响有利.如图7所示,铰点A,D对油缸载荷的有利调整区域为区域2,铰点B的有利调整区域为区域1.

图4 铰点A对α的影响Fig.4 Effect of hinge-point Aonα

图5 铰点B对α的影响Fig.5 Effect of hinge-point Bonα

图6 铰点D对α的影响图Fig.6 Effect of hinge-point Donα

图7 有利调整区域Fig.7 Beneficial adjustment area
此外,铰点C和E包含在上吊臂分离体内部,对下臂油缸不产生影响.铰点A不变,G和F两点无论如何调整,对P1都没有影响.由式(4)可以看出,当γ=0时,X可以达到最大.为了保证作业幅度需求,在图2状态铰点G和F应该尽量靠近边界位置.
2 铰点位置对油缸载荷影响的动力学仿真试验分析
2.1 动力学仿真模型
在实际设计中,除了油缸受力这一因素外,还有油缸行程、工作幅度等因素的制约,而动力学仿真能够将这些因素同时考虑进去.
应用ADAMS软件建立工作装置的动力学模型,仿真工作装置的极限工况.模型中包括图2所示的七个铰点,每个铰点的坐标均作参数化处理,如A点的横坐标设置为变量DV_AX,其他坐标如此类推.此外,还包括边界约束、油缸行程约束、工作幅度约束等.工作装置模型如图8所示.

图8 工作装置三维模型Fig.8 Three-dimensional dynamic model of side container crane
2.2 各铰点位置对油缸载荷的设计研究
以下臂油缸载荷为目标,对七个铰点共14个变量进行设计研究[6],得出各个变量的敏感度,如表1所示.
由表1可知,对下臂油缸载荷影响最大的是DV_AX,DV_BX,DV_BY,DV_DX,DV_DY,DV_GX,DV_GY这七个变量.

表1 设计变量对下臂油缸载荷的敏感度Tab.1 Sensitivity of design variables for down cylinder
2.3 各铰点位置对油缸载荷的试验设计
为了减少计算量同时有利于分析,将最重要的的五个变量DV_AX,DV_BY,DV_DX,DV_DY,DV_GY分为两组进行试验设计[6].
(1)DV_AX,DV_BY与DV_GY
根据实际结构要求,DV_AX值域取为[-1 000,-650],DV_BY值域取为[1 750,2 450],DV_GY值域取为[2 200,2 830].确定等分水平数为8.以下臂油缸受力和工作远度为研究目标,分别进行512次试验,得到512组试验结果.对试验结果进行整理.首先按工作远度进行排序,在合理的远度范围内,均匀地选出八个远度相同的数组(远度变化极小即可认为相同).如对于远度为3 120mm,得到如表2所示数组.

表2 数组示例Tab.2 An example of the arrays
为方便观察变化趋势与规律总结,在不改变各变量自身相对变化趋势的前提下,对各组数据进行整理,使变量之间相对大小相近,以便在同一张图中表示出来.整理所用公式为

式中:U为整理后数值,即相对变化量;Qx为数组中各项(设计变量)的第x个数(即序号);Q1为数组中各项的第1个数;h为缩小因数.数组中DV_AX项的缩小因数h值取为50,DV_BY项的缩小因数h值取为100,DV_GY项的缩小因数h值取为90,油缸载荷项的缩小因数h值取为10 000.对表2中数据利用式(7)进行计算,结果如图10所示.
八个数组整理后的数据绘制成图9~16.图中横坐标表示每个数组中各项序号,纵坐标表示按照式(7)计算得出的相对变化量,正方向表示变大,负方向表示变小.“力”曲线表示油缸载荷.
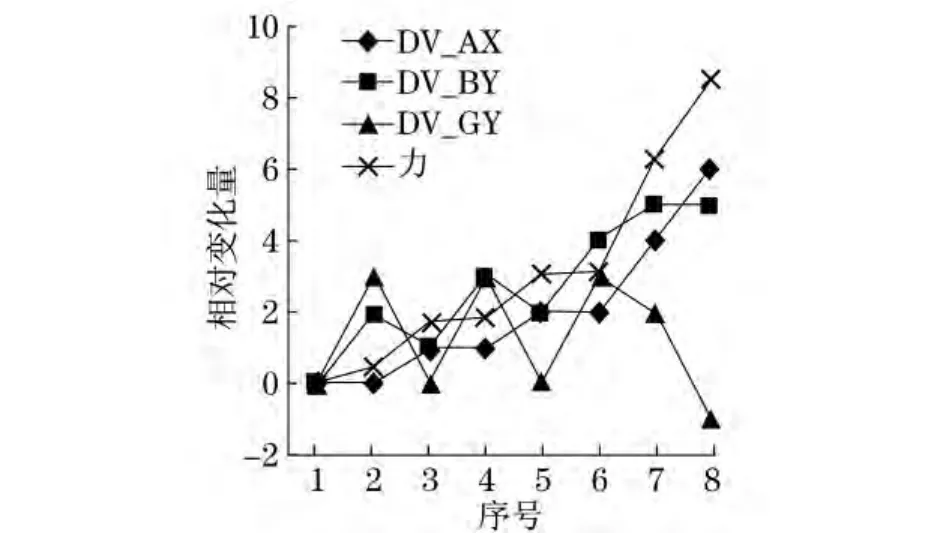
图9 工作远度为2 950mm时各变量变化曲线Fig.9 Variables’curves at a distance of 2 950mm

图10 工作远度为3 120mm时各变量变化曲线Fig.10 Variables’curves at a distance of 3 120mm
由图9~16可见,无论DV_BY与DV_GY如何变化,只要DV_AX变化,力曲线总能随着产生相同的变化.由此可知,DV_AX对下臂油缸影响最显著,下臂油缸载荷随着DV_AX的减小而减小.分析图9中的序号3与4及5与6,图10中的序号3~5,以及其他图中DV_AX折线段的水平部分,可以发现,力曲线的变化趋势与DV_BY相同.所以当DV_AX不变时,下臂油缸载荷随着DV_BY的减小而减小.在变量变化范围内,上述变量对油缸受力的影响都是单调的.DV_GY对下臂油缸载荷影响规律不明显,不难推测出,DV_GY的变化是对应不同的DV_AX和DV_BY为保证相同工作幅度而做出的调整.
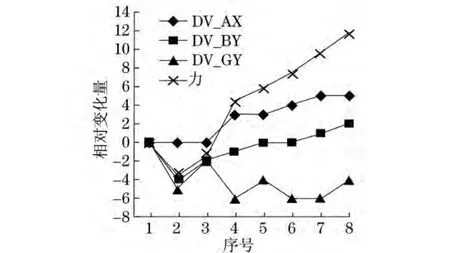
图11 工作远度为3 310mm时各变量变化曲线Fig.11 Variables’curves at a distance of 3 310mm

图12 工作远度为3 600mm时各变量变化曲线Fig.12 Variables’curves at a distance of 3 600mm
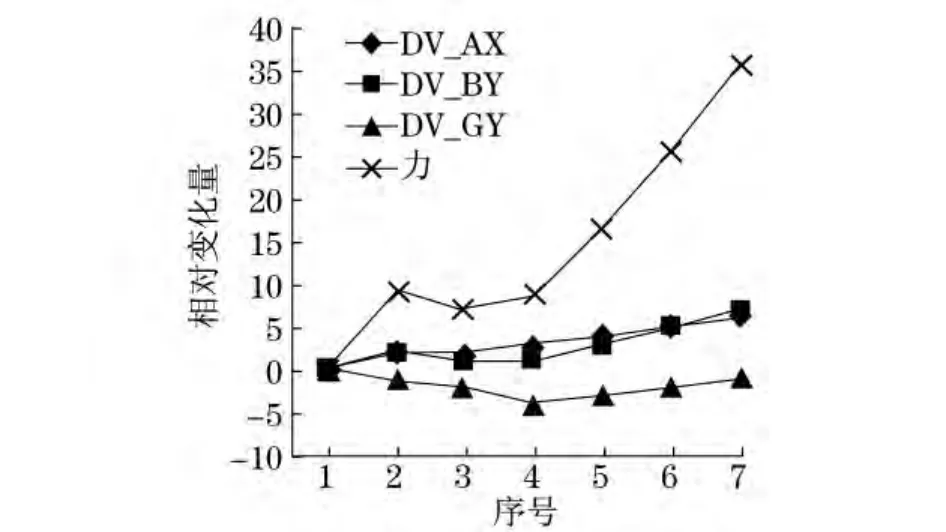
图13 工作远度为3 750mm时各变量变化曲线Fig.13 Variables’curves at a distance of 3 750mm
(2)DV_DX,DV_DY与DV_GY
根据实际结构要求,DV_DX值域取为[200,550],DV_DY值域取为[1 850,2 340],DV_GY值域取为[2 200,2 830].然后采用组(1)的方法进行处理,得到图17~24.图中横坐标表示每个数组中各项序号,纵坐标表示按照式(7)计算得出的相对变化量,正方向表示变大,负方向表示变小.

图14 工作远度为3 950mm时各变量变化曲线Fig.14 Variables’curves at a distance of 3 950mm
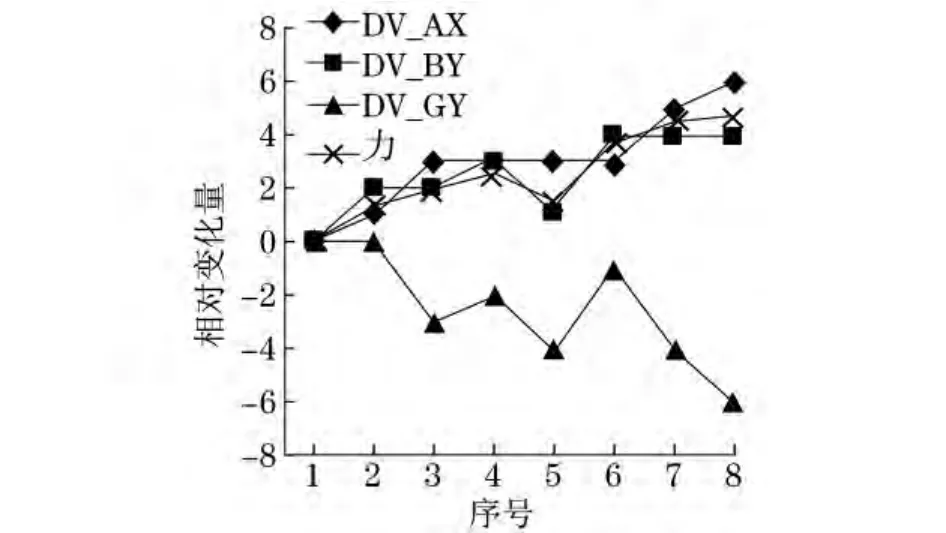
图15 工作远度为4 230mm时各变量变化曲线Fig.15 Variables’curves at a distance of 4 230mm

图16 工作远度为4 410mm时各变量变化曲线Fig.16 Variables’curves at a distance of 4 410mm
由图17~24可以发现,无论DV_DY与DV_GY如何变化,只要DV_DX变化,力曲线总能随着产生相同的变化.可见DV_DX对油缸影响最显著,DV_DX越小,下臂油缸受力越小.DV_DX减小时,DV_DY也要减小,可以推测出,这是为了满足工作幅度不变的要求.从图17中的序号3~5和6~8,图18中的序号3~7,以及其他图中DV_DX折线段的水平部分,可以发现,力曲线的变化趋势与DV_DY相反.可见DV_DX不变时,DV_DY越大,下臂油缸受力越小.在变量变化范围内,上述变量对油缸受力或工作幅度的影响都是单调的.与组(1)情况相同,DV_GY对下臂油缸载荷影响规律不明显,DV_GY的变化是对应不同的DV_DX和DV_DY为保证相同工作幅度而做出的调整.

图17 工作远度为3 050mm时各变量变化曲线Fig.17 Variables’curves at a distance of 3 050mm

图18 工作远度为3 150mm时各变量变化曲线Fig.18 Variables’curves at a distance of 3 150mm

图19 工作远度为3 250mm时各变量变化曲线Fig.19 Variables’curves at a distance of 3 250mm
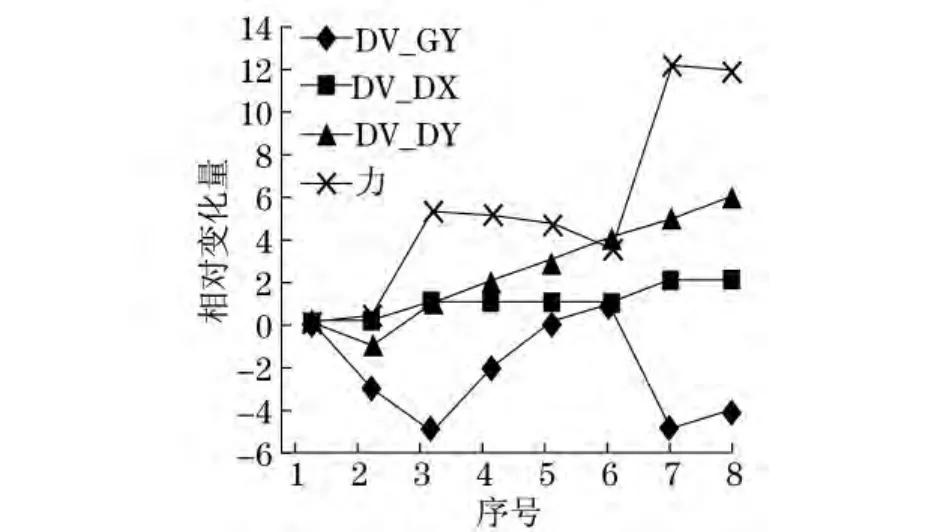
图20 工作远度为3 440mm时各变量变化曲线Fig.20 Variables’curves at a distance of 3 440mm
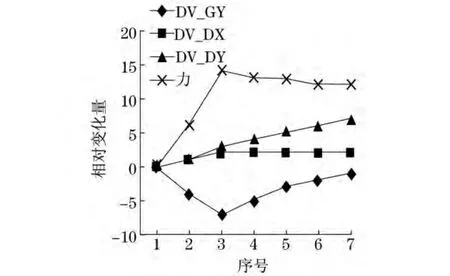
图21 工作远度为3 650mm时各变量变化曲线Fig.21 Variables’curves at a distance of 3 650mm

图22 工作远度为3 850mm时各变量变化曲线Fig.22 Variables’curves at a distance of 3 850mm

图23 工作远度为4 060mm时各变量变化曲线Fig.23 Variables’curves at a distance of 4 060mm
3 理论分析结果与仿真试验结果对比
对照图2可以看出,理论分析和仿真试验两种方法中主要铰点A,B,D对下臂油缸载荷影响趋势的分析结果是一致的,铰点G“主要影响工作幅度”的理论也相同.通过理论分析可知,铰点C,E对下臂油缸载荷不产生直接影响,可见理论分析更加全面.通过仿真试验可知,铰点A的横向位置和铰点D的横向位置对下臂油缸的影响更显著,可见仿真试验能得出各铰点的影响程度,而且试验数据更直观.理论分析与动力学仿真分析既是相互验证,又是相互补充.

图24 工作远度为4 260mm时各变量变化曲线Fig.24 Variables’curves at a distance of 4 260mm
4 结论
(1)下臂油缸下铰点对下臂油缸所受载荷影响非常大,位置越靠左,下臂油缸所受载荷越小.在作业幅度满足要求的条件下,应将此铰点尽可能靠左侧设计.
(2)下吊臂下铰点向下侧或右侧移动,都会使下臂油缸受力减小.因此,在设计过程中,应该在结构允许的条件下,尽可能使此铰点偏向右下侧,靠近边界,这样对下臂油缸载荷的影响非常有利.
(3)下臂油缸上铰点距离下吊臂下铰点越远,下臂油缸载荷越小.因此,在满足作业幅度与结构要求的条件下,应尽量拉大下臂油缸上铰点与下吊臂下铰点之间的距离.
(4)上臂油缸的上下铰点、上吊臂的上下铰点对下臂油缸载荷均不产生直接影响,而主要影响作业幅度.
本文采用的理论分析与仿真试验相结合的方法可以为同类问题的研究提供参考,得出的结论可以为结构设计人员在铰点位置设计及后续调整时提供指导,研究内容还可以为铰点优化平台的开发提供理论依据与数据库支持.
[1]肖献法.我国应大力发展公路集装箱自装卸系统[J].商用汽车,2002(10):34-37.XIAO Xianfa.Self-loading and tipper system of road container should be developed in China[J].Commercial Vehicle,2002(10):34-37.
[2]成凯.集装箱自装卸运输车用折臂式起重机的运动和受力分析[J].建筑机械,1995(8):12-14.CHENG Kai.The movement and force analysis of fold-arm hoist on self-loading and unloading container trailer[J].Construction Machinery,1995(8):12-14.
[3]成凯,秦四成,黄海东.集装箱自装卸半挂运输车[J].工程机械,1996(10):3-4.CHENG Kai,QIN Sicheng,HUANG Haidong.Self-loading and unloading container trailer[J].Construction Machinery and Equipment,1996(10):3-4.
[4]冯晓梅,詹隽秀.集装箱侧面吊起重机构优化设计[J].机械设计,2004,21(12):21-25.FENG Xiaomei,ZHAN Juanxiu.Optimization design on lifting mechanism of the side crane[J].Journal of Machine Design,2004,21(12):21-25.
[5]张子达,邹广德,刘刚.装载机铰接系统铰点位置对铰点载荷的影响[J].吉林工业大学学报,1997(2):68-72.ZHANG Zida,ZOU Guangde,LIU Gang.Effect of the location of articulated joints of wheel loader on articulated joint load [J].Journal of Jilin University of Technology,1997(2):68-72.
[6]MSC.Software.ADAMS/VIEW 高级培训教程[M].北京:清华大学出版社,2004.MSC.Software.Advanced ADAMS/VIEW training[M].Beijing:Tsinghua University Press,2004

