移动质量－梁耦合系统的动态响应分析

秦仙蓉，张立冬，张 氢，孙远韬

（同济大学 机械与能源工程学院，上海 201804）

移动质量作用下梁的动态响应问题在各个工程领域都很常见，如重物－桥吊系统的耦合振动、车－桥耦合系统的振动及火炮后座等，这些振动系统往往可以简化为移动质量－梁耦合系统.早期的理论模型仅仅研究集中力作用下等截面梁的动态响应，研究者多采用振型叠加法或积分变换的方法获得解析解，将解析解与试验结果对比，得出移动载荷相对于梁的质量较小时可以忽略移动载荷惯性力对梁动态响应影响的结论［1－2］.长期以来，这一结论在工程领域被广泛接受.随着机械系统向着高速、重载的趋势发展，工程实际中遇到越来越多的具有大质量、高速度的移动载荷作用在梁上的问题，这就要求模型中不能忽略移动载荷惯性力的影响.由于载荷是移动的，而且载荷本身也是具有质量的系统，这使得移动质量－梁耦合系统的动态特性随着载荷位置的移动而不断变化.耦合系统振动方程的系数矩阵是时变的，这给理论分析带来了极大的困难.研究表明，具有时变系数的动力学方程很难得到解析解，通常需要通过有限元方法获得数值解［3－4］.

本文考虑移动质量惯性力对梁动态响应的影响，建立具有时变系数的移动质量－梁耦合系统振动方程，采用Newmarkβ逐步积分法，对不同运动状态移动质量作用下梁的动态响应进行数值模拟.

1 移动质量－梁耦合系统建模

考察如图1所示的移动质量－梁耦合系统，长度为L的简支梁上有一质量为M，以初速度v0，匀加速度a向前运动的物体.梁单位长度的质量为m，抗弯刚度为EI，梁上x处在t时刻的瞬时挠度为u（x，t），其值设为小量.梁的科氏力、向心力以及梁的阻尼对耦合系统响应的影响很小，故此处均忽略不计，从而可以写出梁的振动方程为

式中：用撇表示对x的导数，用圆点表示对t的导数；和Mau′分别为牵连惯性力和相对惯性力对梁横向振动的影响项［5］；g为重力加速度；δ为狄拉克函数；s＝v0t＋（1／2）at2为移动质量走过的路程.设

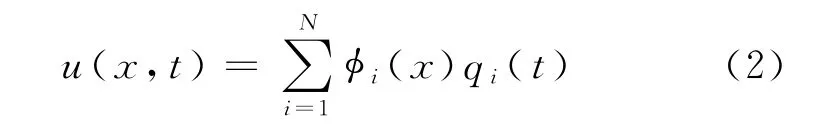
式中：φi（x）（i＝1，2，…，N）为简支梁的第i阶振型的振型函数，qi（t）为第i阶振型的广义坐标.将式（2）代入式（1）有

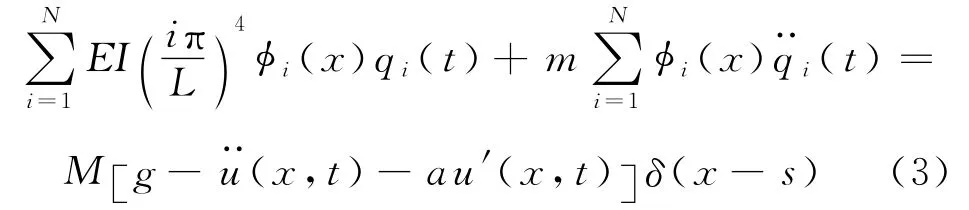
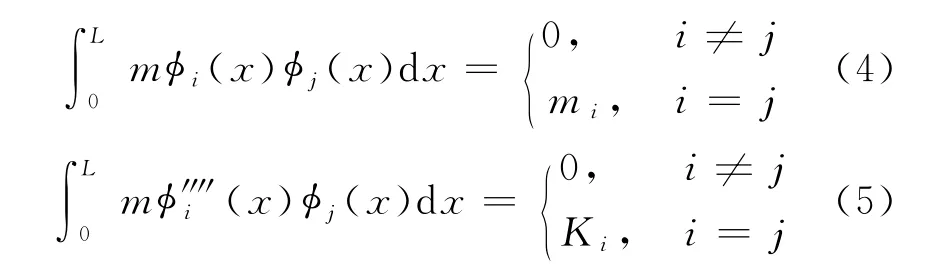
式中：mi，Ki分别为梁的第i阶模态主质量和第i阶模态主刚度.所以有

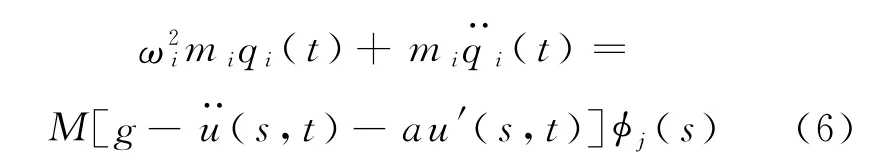
又因为有

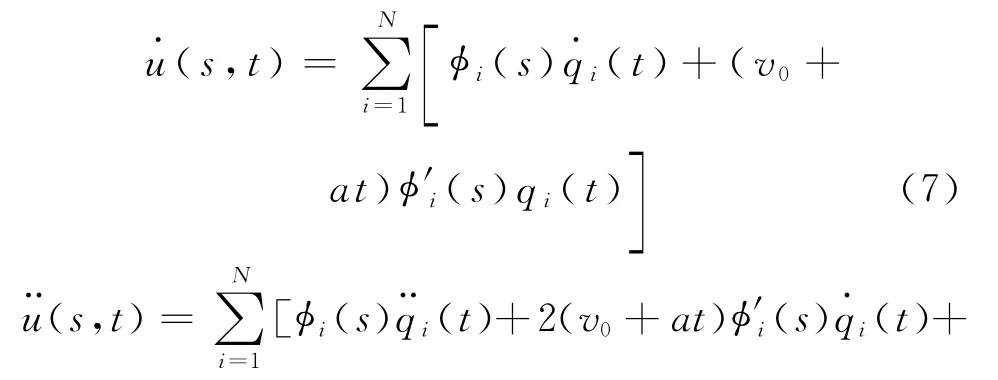
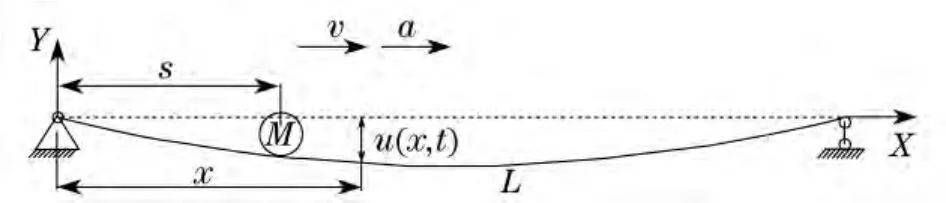
图1 耦合系统的力学模型Fig.1 Dynamic model of the coupling system

于是式（6）可以写为

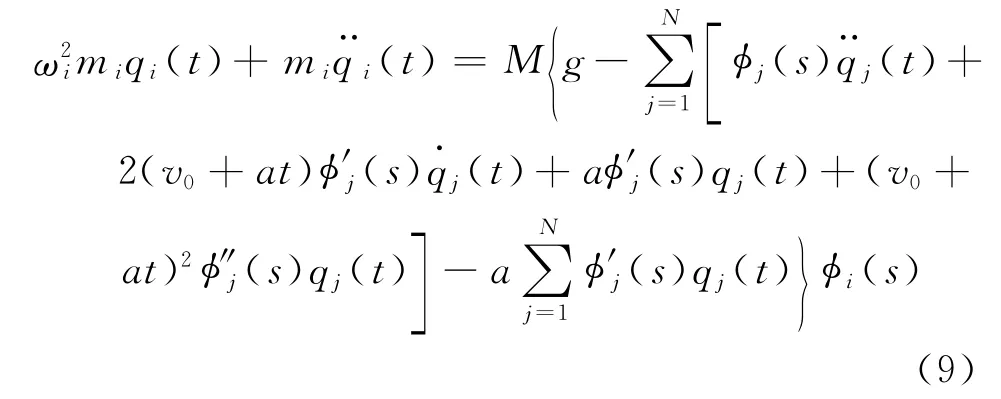
式（9）也可以写成如下的矩阵形式：

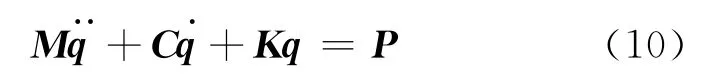
其中，

式中：Φ（s）为梁的模态函数矩阵，Φ′（s）和Φ″（s）分别是Φ（s）关于移动质量的位置坐标s的一阶和二阶导数矩阵.

从理论推导过程可以看出，上述计算对梁的边界条件未加任何限制，只要能写出梁的模态函数的解析表达式就能应用，因而适用范围较广.

2 方程求解

由于移动质量在梁上的位置不断变化，方程（10）中的质量矩阵M、阻尼矩阵C、刚度矩阵K都在随时间不断变化，这使得移动质量－梁的耦合系统动力平衡方程组成为一个二阶时变系数的微分方程组，同时方程组的系数矩阵M，C，K还随着运动参数v0和a的变化而变化.对于此类微分方程组，最有效、最常见的方法是逐步积分法.

逐步积分法的基本原理是人为假定一个反应规律，通过每一个微小时间增量Δt来逐步计算整个结构体系的反应.在计算中通常忽略体系在Δt时间内的不平衡，而体系的时变特性则是由一连串不断改变的时不变体系来无限逼近.目前，常用的逐步积分法主要有线性加速度法、Willsonθ法以及Newmarkβ法.此处采用Newmarkβ法.

设t＋Δt时刻三组未知量和它们满足动力学方程式（10），即

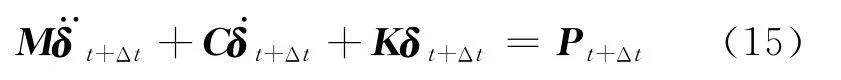
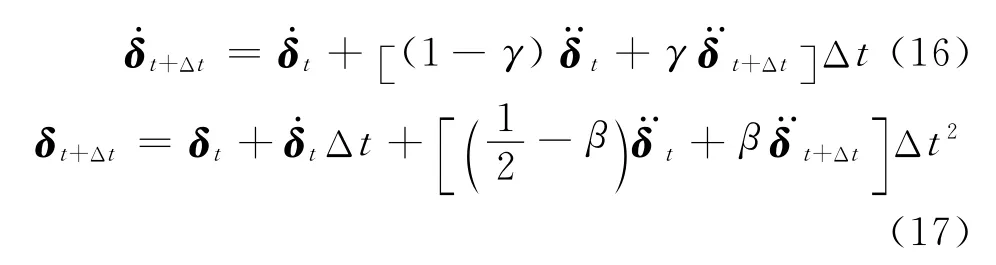
式中：γ，β为 Newmark参数.式（15）～（17）是Newmarkβ法的基本公式，将式（16）和（17）整理，代入式（15），得到t＋Δt时刻的加速度、速度和位移分别为

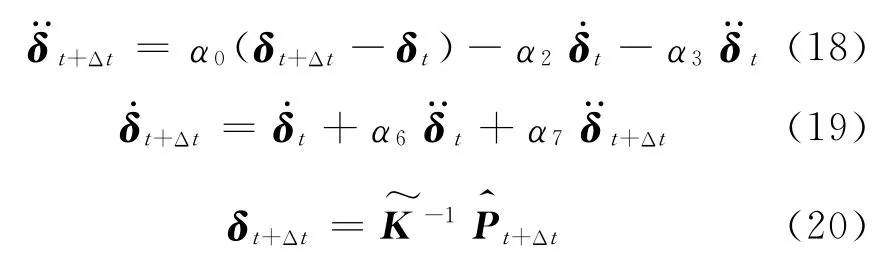
其中，

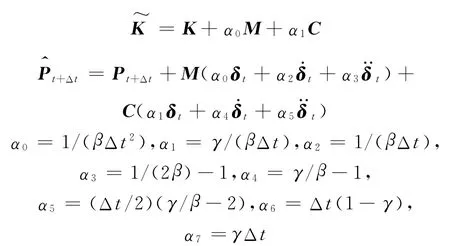
3 移动质量作用下梁的动力响应分析

参照某型号塔式起重机起重臂参数，取移动质量M＝3 000kg，梁单位长度质量m＝126kg·m－1，L＝65m，EI＝1.26×108N·m2.取积分步长Δt＝0.01s，Newmark参数γ＝0.25，β＝0.5.

首先分析移动质量在加速度为零时，初速度对梁跨中挠度的影响.图2给出了移动质量分别以0.15，0.50，1.00m·s－1的初速度匀速通过简支梁时，梁跨中挠度的变化规律.可以看出，移动质量作用下梁的挠度曲线是以一定频率围绕静挠度曲线的一种类正弦波动.随着速度的增加，波动的幅值越来越大，频率越来越低，周期越来越长.这是由于移动质量参与振动，使振动频率略有降低［6］.从局部放大图中还可以知道，梁最大挠度并不总是发生在移动质量运动到梁跨中位置处，而是在跨中位置的前后.

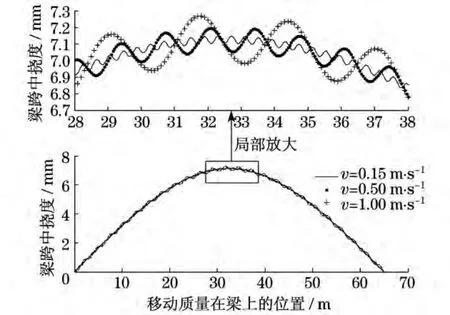
图2 不同速度移动质量作用下梁跨中挠度Fig.2 Deflection of beam subjected to the moving mass with variable velocity

移动质量加速度对梁跨中挠度的影响如图3所示.可以看出，移动质量以不同的加速度过梁与匀速过梁时梁跨中挠度曲线相似.在同一初速度的情况下，移动质量加速运动时梁跨中挠度比匀速运动时梁跨中挠度要大，且加速度越大，梁跨中位置的最大挠度也越大.移动质量加速运动时，耦合系统的振动相对平稳.同时可以看出，在匀加速运动的移动质量作用下，梁跨中挠度响应曲线的峰值沿横轴向后偏移，说明由于移动质量惯性力的影响，梁最大挠度并不是发生在移动质量运动到梁跨中位置处，在移动质量的加速度不能忽略时，这种影响尤甚.

对于移动质量减速运动的情况，只需要将加速度以负值代入式（10）计算即可.但要注意的是，如果移动质量在梁上减速到零，则只能按照式（10）计算到移动质量速度减到零的时刻，之后移动质量将停止在梁上与梁一起自由振动.

对于本文选取的初速度0.15，0.50，1.00 m·s－1，移动质量在减速度作用下速度很快减小到零随后便静止在梁上，同时移动质量运动的路程也较小，停止在梁上的位置距梁跨中还有一定距离.由力学常识可知，这种情况下梁跨中挠度值会比较小.

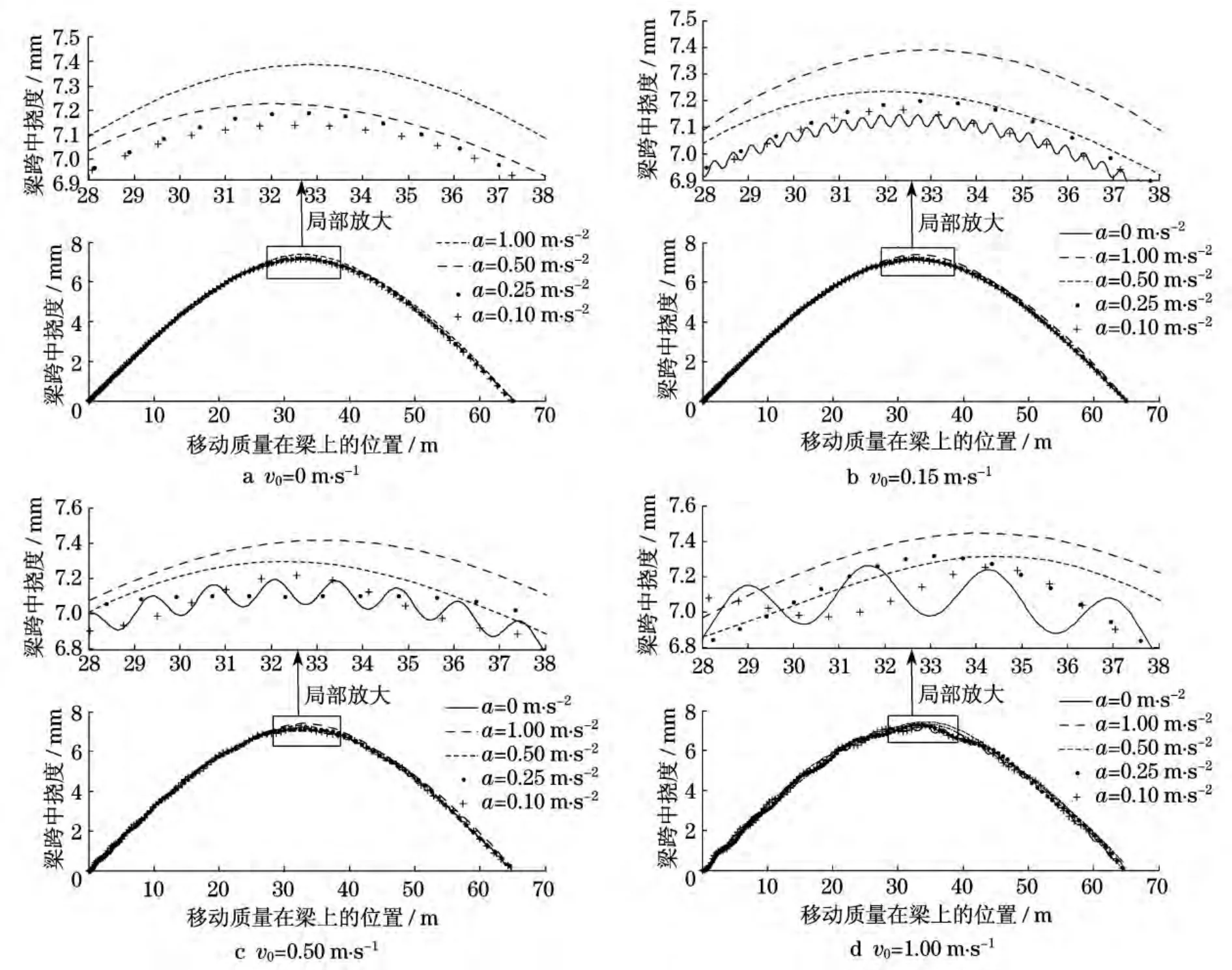
图3 移动质量加速度对梁跨中挠度的影响Fig.3 Effect of acceleration for the moving mass on the deflction

图4 移动质量减速度对梁跨中挠度的影响Fig.4 Effect of deceleration for the moving mass on the deflction

图4揭示了移动质量的减速度对梁跨中挠度的影响.由图可见，相比于加速情况，在移动质量减速运动情况下，梁跨中挠度较小，且减速度绝对值越大，梁跨中挠度值越小.这与加速运动时恰恰相反.这是由于当移动质量加速运动时，它受到梁作用的与其运动方向一致的摩擦力，同时梁受到移动质量施加的反作用力，这个力可以看作是作用在梁上的轴向压力，该压力将在梁内产生附加弯矩，从而使梁的挠度加大.相反，当质量减速运动时，梁将受到轴向拉力，该拉力在梁内产生的附加弯矩使梁的挠度减小［5］.

4 结论

（1）在移动质量具有较大速度和较大加速度的情况下不能忽略其惯性力影响.

（2）移动质量作用下梁跨中挠度曲线是以一定频率围绕静挠度线的一种类正弦波动曲线.随着速度的增加，振动的幅值越来越大，频率越来越低，周期越来越长.

（3）移动质量以不同的加速度与匀速过梁时梁跨中挠度曲线相似.在同一初速度的情况下，移动质量加速运动时梁跨中挠度比匀速运动时梁跨中挠度要大，且加速度越大，梁跨中位置的最大挠度也越大.移动质量加速运动时，耦合系统的振动相对平稳.

（4）梁最大挠度并不总是发生在当移动质量位于梁跨中时，而是发生在移动质量经过跨中位置的前后时刻.移动质量对梁挠度的影响与速度、加速度等多个因素有关，是一个相对复杂但有一定规律可循的过程.

［1］HILAL M A.Vibration analysis of beams with general boundary conditions traversed by a moving force［J］.Jounal of Sound and Vibration，2002，229（2）：377－388.

［2］BIERER T，BODE C.A semi－analytical model in time domain for moving loads ［J］.Soild Dynamics and Earth Quake Engineering，2007，27：1073－1081.

［3］WU J J，WHITTAKER A R，CARTMELL M P.The use of finite element techniques for calculating the dynamic response of structures to moving loads［J］.Computers and Structures，2000，78：789－799.

［4］WU J J，WHITTAKER A R，CARTMELL M P.Dynamic responses of structures to moving bodies using combined finite element and analytical methods［J］.International Journal of Mechanical Sciences，2001，43：2555－2579.

［5］彭献，刘子健，洪家旺.匀变速移动质量与简支梁耦合系统的振动分析［J］.工程力学，2006，6（6）：25－29.PENG Xian，LIU Zijian，HONG Jiawang.Vibration analysis of a simply supported beam under moving mass with uniformly variable speeds ［J］.Engineering Mechanics，2006，6（6）：25－29.

［6］肖新标，沈火明.移动荷载速度对简支梁动态响应的影响［J］.西南交通大学学报，2002，37（s）：35－38.XIAO Xinbiao，SHEN Huoming.Effect of speed of moving loads on dynamic responses of simply supported beams ［J］.Journal of Southwest Jiaotong University，2001，37（s）：35－38.