射影几何中不变元素的特征值特征向量解释

游学民，樊孝菊



射影几何中不变元素的特征值特征向量解释

游学民，樊孝菊

(湖北文理学院 数学与计算机科学学院，湖北 襄阳 441053)

将射影几何中的不变元素采用矩阵特征值与特征向量进行解释，并指出其不变元素即为矩阵的特征向量，明晰了不变元素的涵义.

射影几何；不变元素；特征值；特征向量

矩阵特征值与特征向量在不同环境下有着不同的解释，在《高等代数》中有着其环境下的解释，在《射影几何学》中也有其特有的解释. 本文将结合矩阵特征值与特征向量对射影几何中的不变元素本质进行阐释.

1 基本定义

定义1[1]经射影变换后元素的映象与原象重合，这种元素称为射影变换的不变元素.

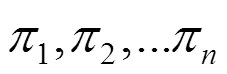
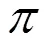
2 特征值、特征向量几何解释

3 主要成果

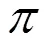
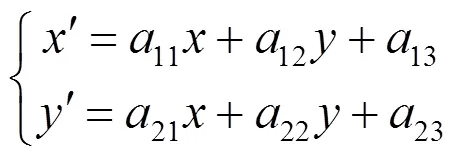
引理2[3-4]两不变点的连线是一条不变直线；对偶地，两不变直线的交点是一不变点.

证明：设不变直线为

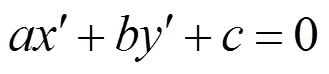
(3)

.

定理2 二维射影变换

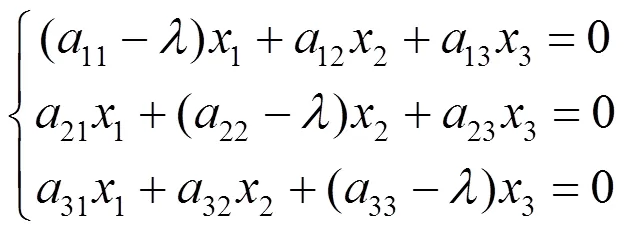
因此当式(6)有解时，二维射影变换(4)才有不变元素.

定理3 在二维射影变换有不变元素条件下，若式(6)有三个不同的特征值时，变换(4)有三个不共线的不变点，其不变点为特征值对应的特征向量，同时有三条不变直线，不变直线由任意两特征向量确定.

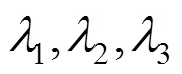
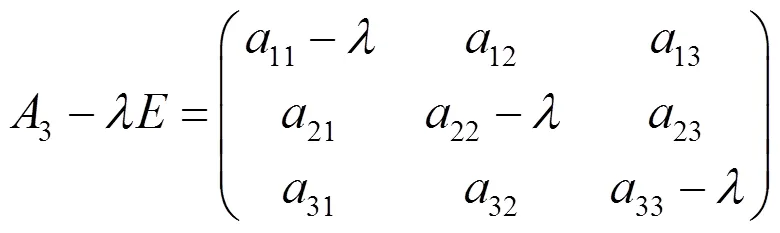
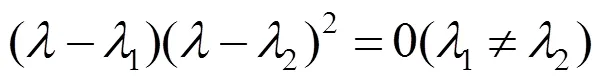
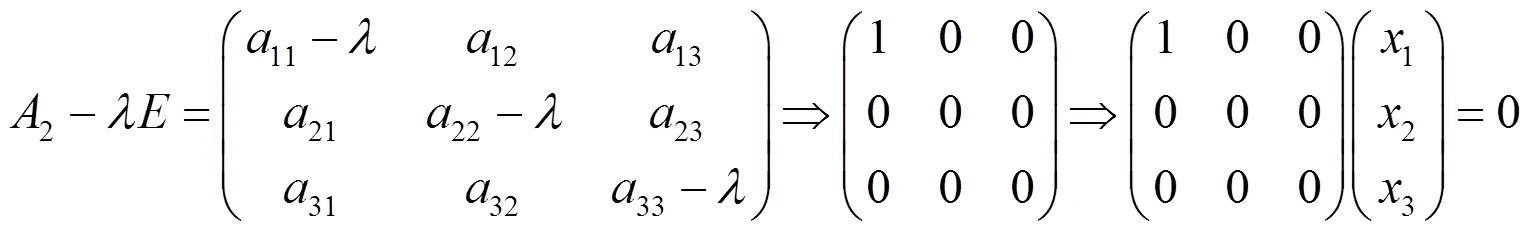
证明类似定理4.

[1] 梅向明, 刘增贤, 王汇淳, 等. 高等几何[M]. 3版. 北京: 高等教育出版社, 1998.

[2] 北京大学数学系几何与代数教研室前代数小组. 高等代数[M]. 王萼芳, 石生明, 修订. 3版. 北京: 高等教育出版社, 2003.

[3] 周明旺. 平面射影几何中二维射影变换不变元素的分布[J]. 通化师范学院学报, 2010(4): 13-15.

[4] 郭玉琳. 射影平面上不动元素的若干性质[J]. 高等数学研究, 2005(1): 47-48, 55.

Interpreting Characteristic Value and Characteristic Vector in Projective Geometry

YOU Xueming, FAN Xiaoju

(College of Mathematical and Computer Sciences, Hubei University of Arts and Science, Xiangyang 441053, China)

It explains the invariant element in projective geometry via matrix eigenvalues and characteristic vector, and it points out that the invariant element is the characteristic vector of matrice, and clears the meaning of the invariant element.

Projective geometry; Invariant element; Characteristic value; Characteristic vector

2014-05-15;

2014-06-16

湖北省教育科学“十二五”规划重点课题(2011A056); 湖北文理学院教研项目(JY201261)

游学民(1967— ), 男, 湖北安陆人, 湖北文理学院数学与计算机科学学院副教授.

O185

A

2095-4476(2014)08-0016-03

(责任编辑：饶 超)