非线性结构系统能控性参数分析

马 强，汪 云，姜 伟



非线性结构系统能控性参数分析

马 强1，汪 云1，姜 伟2

(1. 湖北文理学院 机械与汽车工程学院，湖北 襄阳 441053；2. 华中科技大学 机械科学与工程学院，湖北 武汉 430074)

文章研究了一类非线性组合系统的结构能控性，将非线性系统模型置于非交换环上用以得到非线性系统的传递函数(矩阵). 根据频域上线性系统能控的系统传递函数不存在零极点抵消的判据，获得非线性系统结构能控的条件，并用实例证明所获得的判据对分析非线性系统结构能控性是可行的.

非线性系统；结构能控性；传递函数；非交换环；多项式环

能控性概念最早由Kalman 在线性系统分析中提出，它是描述线性系统特性的一个重要概念. 对于状态空间描述的线性时不变系统，能控性可以用秩条件表示，即rank(B, AB, …，AB)=. 一个能控的线性系统一般可以通过状态反馈使得系统稳定，因此能控性分析在线性系统理论中有重要作用. 而对于非线性系统能控性研究也已经有了较多成果.

Sussmann与Jurdjevi[1]分析了非线性系统的能控性. 对于非线性系统，他们指出可达集的几何结构实际上是一个子流形. 同时对于某个点的可达集在什么时候具有非空内部给出了一个完整答案. Sussmann[2]利用Lie代数工具对具有标量输入的非线性系统进行分析，并给出了系统能控的充分条件. Stefani[3]研究了标量输入的非线性系统，并给出了系统局部能控的条件. Zheng与Cao[4]将传递函数概念引入到非线性系统分析中，为研究非线性系统特性提供了一个新的代数工具. 利用传递函数工具分析非线性系统，可以得到系统的全局性质，而不是某个工作点附近的近似特性. 同时还可以得到系统的输入输出描述，这为组合非线性系统性质分析指出了一个方向. Zheng等[5]利用传递函数方法研究了非线性系统的能控性. Halas与Kotta[6]将传递函数应用到非线性离散系统，并研究其性质. Halas[7]利用传递函数研究了非线性时滞系统.

本文的工作主要是将参量空间引入到非线性系统中，利用传递函数工具得到SISO非线性系统的结构能控性条件. 一个结构能控的非线性系统，当参数在参量空间中任意取值时，得到的具体系统几乎一定是能控的. 与Fradellos等[8]的分析不同，本文的重点在于分析参数对系统性质的作用或影响，而Fradellos等的工作在于分析非线性系统在扰动作用下系统依然保持能控性，则称之为结构能控的.

1 非线性系统的传递函数

对于如下一个由状态空间模型描述的SISO非线性系统

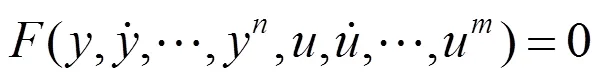
其中函数F也是meromorphic函数.

对于一个SISO系统，它一般可以由一个高阶输入输出微分方程描述

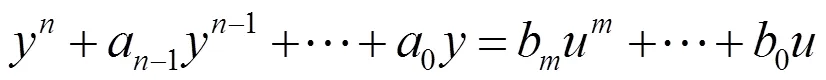
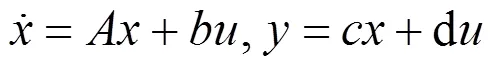
对于高阶输入输出方程(3)与状态空间描述(4)之间是等价的. 但是对于非线性系统而言，一般来说每个状态空间描述有一个与之相对应的高阶输入输出方程，但反之却不尽然. 本文主要考虑SISO的输入输出微分方程所描述的系统(2).

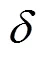
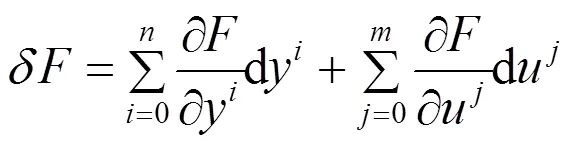
对进行求导运算有

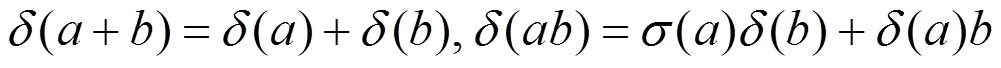
这样的一个多项式环称之为skew polynomial环.

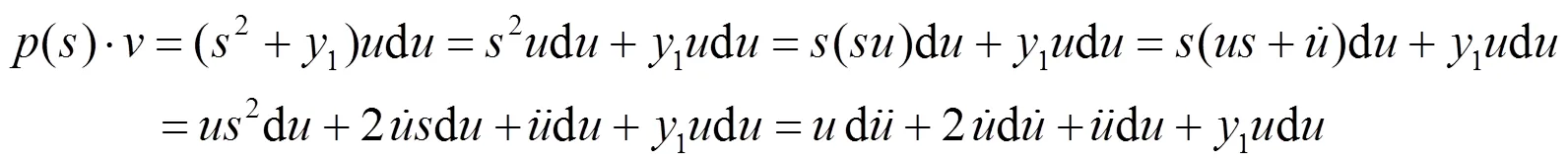
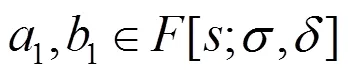
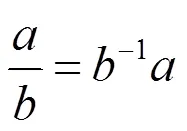
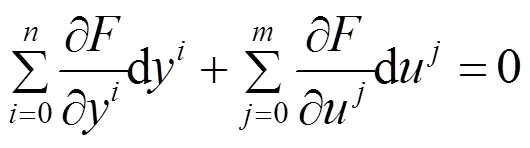
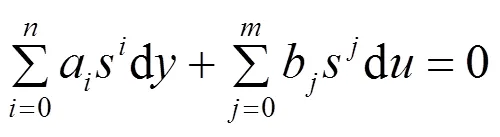
进一步得到

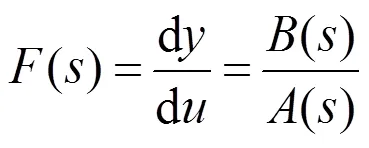
等式(9)即为SISO非线性系统的传递函数.

2 组合非线性系统的结构能控性

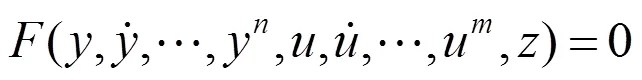
定义1 令K(z)表示所有的含有参量z的meromorphic函数域，称之为多元meromorphic函数域或简称为多元函数域.

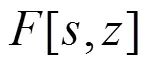
根据微分代数的定义，一个非线性系统称之为能控的是指其不存在自治变量.

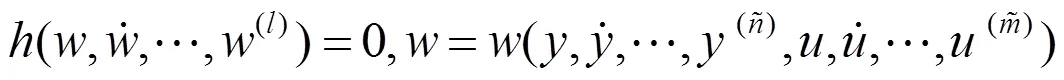
由(6)-(9)式可知非线性系统(10)的传递函数为

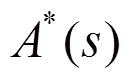
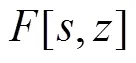
对于非线性系统的组合方式也可以分为串联，并联与反馈连接. 本文主要关注串联与并联连接方式.

考虑由(10)式描述的两个非线性系统：

∑1，它的传递函数表示为：

∑2，它的传递函数表示为：

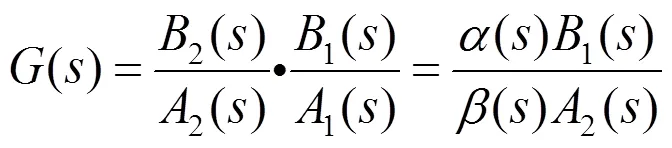
其中根据引理2有

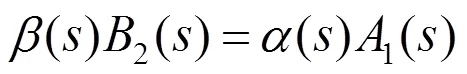
备注1 考虑到组合方式的不同及其非交换因素，对于组合系统∑21而言，其传递函数与∑12是不同的，因此以下引理成立：

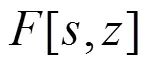
对于并联组合系统，同样考虑(14)(15)两个子系统，那么并联组合系统的传递函数可以表示为：

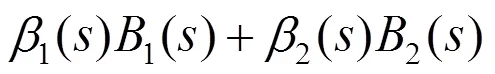
定理2 串联组合系统是结构能控的，当各子系统是结构能控的且组合系统传递函数分子与分母无域K上左公因子.

图1 一个RLC无源网络

考虑串联方式∑12，则组合系统的传递函数为

式(23)经过非交换乘法运算后变为

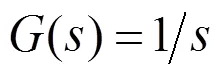
所以串联组合系统∑12是结构能控的. 如果考虑串联方式∑21，则组合系统的传递函数为

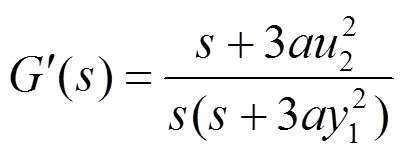
显然串联组合方式∑21的传递函数无左公因子，所示串联组合系统∑21是结构能控的.

现在考虑两个子系统的参数不同，则可以重新表示为：

仅考虑串联组合方式∑，则该组合系统的传递函数可以表示为：

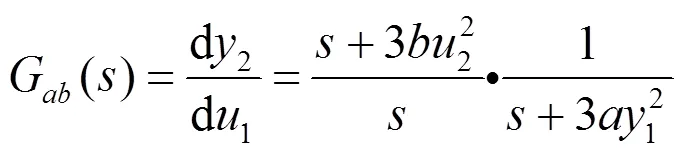
3 结语

本文利用非线性系统的传递函数和参量空间分析了SISO非线性系统的结构能控性，并对串联与并联组合系统的能控性进行了研究. 由于非线性系统的传递函数运算满足非交换法则，所以一般线性系统频域上的能控性条件不能简单扩展到非线性系统研究中来. 本文中定义了新的多元函数域()及多元skew polynomial，为研究非线性系统的结构性质建立的完善的数学框架. 研究非线性系统的结构性质，可以了解参数对系统性质的影响和作用，为非线性系统的分析和设计提供理论依据.

[1] Sussmann H J, Jurdjevic V. Controllability of nonlinear systems[J]. Differential Equations, 1972(12): 95-116.

[2] Sussmann H. Lie brackets and local controllability: a sufficient condition for scalar input Systems[J]. SIAM Journal on Control and Optimization, 1983(21): 686-713.

[3] G. Stefani. On the local controllability of a scalar input control system: Theory and Applications of Nonlinear Control Systems[M]. Amsterdam: A. Lindquist eds, 1986: 167-176.

[4] Zheng Y, Cao L. Transfer function description for nonlinear systems[J]. Journal of East China Normal University: Natural science, 1995(2): 15-26.

[5] Zheng Y, Willems J, Zhang C. A polynomial approach to nonlinear system controllability[J]. IEEE Transactions on Automatic Control, 2001(46): 1782–1788.

[6] Kotta Halas. Extension of the concept of transfer function to discrete-time nonlinear control systems[M]. Greece: European control press, 2007.

[7] Halas M, algebras Ore. A polynomial approach to nonlinear time-delay systems[M]. Nantes: on time-delay systems, 2007.

[8] Fradellos G. Rapanakis M, Evans F.J. Structural controllability in non-linear systems[J]. Inter. J. Systems Science, 1977(8): 915-932.

[9] Qiang Ma. Some Results on Structural Controllability of Nonlinear Systems[C]. Proc. of International Conference on Intelligent Systems Design and Engineering Appilications (ISDEA2010), 2010: 391-394.

Parameters for Controllability in Nonlinear Structured Systems

MA Qiang1, WANG Yun1, JIANG Wei2

(1. School of Mechanical and Automotive Engineering, Hubei University of Arts and Science, Xiangyang 441053, China；2.School of Mechanical Science and Engineering, Huazhong University of Science and Technology, Wuhan 430074, China)

This paper investigates the structural controllability of a class of nonlinear composite system. The transfer function (matrix) of nonlinear composite systems is obtained by putting the nonlinear system model on non-commutative ring. Structural controllability conditions of nonlinear systems are presented according to the criterion of linear system structural controllability in frequency domain. Some examples are used to testify the presented conditions finally

Nonlinear systems; Structural controllability; Transfer function; Non-commutative ring; Polynomial ring

2014-07-15

国家自然科学基金项目(51307047); 国家863项目(2012AA111100)

马 强(1981— ), 男, 河北定州人, 湖北文理学院机械与汽车工程学院讲师, 博士.

TH123+.1

A

2095-4476(2014)08-0005-06

(责任编辑：徐 杰)