并行计算在MOEA/D-EGO算法中的应用

马永格，吴钊



并行计算在MOEA/D-EGO算法中的应用

马永格1,2，吴钊1

(1. 湖北文理学院 数学与计算机科学学院，湖北 襄阳 441053；2. 中国地质大学 计算机学院，湖北 武汉 430074)

在MOEA/D-EGO算法中，当建模样本点集合元素太多和种群规模较大时，会导致算法运行时间过长. 为了减少MOEA/D-EGO算法的运行时间，文章对MOEA/D-EGO算法的建模过程和种群优化过程同时并行化. 在综合考虑实验条件限制的情况下，使用了基于主从式的并行模型，模型在充分考虑计算机资源的使用效率与负载均衡等因素下，增加了主进程的任务，主进程不仅需要为子进程分配计算任务、分发数据、进行算法配置、收集子进程返回的计算结果，还需要参与子进程的任务，完成与子进程相当量的计算任务. 实验结果表明文章的并行MOEA/D-EGO算法能有效求解多目标优化问题，且能够大幅缩短算法运行时间.

MOEA/D-EGO算法；并行计算；候选解；种群优化

由于MOEA/D-EGO[1]算法本身的以建模算法评价候选解策略和种群优化过程都是针对昂贵评价优化问题所设计，在求解某些类别的优化问题上已经是目前的最优的算法. 所以，使用并行计算[2]对MOEA/D-EGO算法并行化，以此来减少算法运行时间是更加合理的途径.

近年来，在使用并行演化算法来缩短算法在多目标优化问题上的求解时间，也被越来越多的学者所研究. 在2011年D.Logofatu和M.Gruber[3]结合MapReduce[4]与多目标演化算法用于数据压缩实例求解，并将算法应用于超大规模集成电路中寻找最小测试集的问题中，该框架仅适用于含大数据处理的优化问题. 2013年李晖教授[5]提出了一种新型的基于主从模式的并行演化算法大幅度的缩短了演化算法在继电器参数优化问题中的计算时间. 2013年Si-Jung Ryu, Jong-Hwan Kim[6]则针对在多目标量子演化算法中，基于非支配排序和拥挤距离分配计算时间过长的问题，使用了GPU的分布计算能力，但是算法仅适用于基于Pareto前沿的多目标演化算.

研究资料表明，在很多并行计算系统中，计算结点的CPU平均利用率仅达9%[7]. 通过实验分析，本文发现在MOEA/D-EGO算法的运行过程中，计算系统中的资源至少有1/3 到2/3 的时间是空闲的，利用这些空闲的处理能力并行求解较大的计算问题或者并行执行多个作业，可以大大缩短问题的求解时间.

1 MOEA/D-EGO并行性分析

在MOEA/D-EGO算法中，主要有种群初始化、候选解评价、种群优化过程三个大的部分，种群初始化和种群优化过程是基于MOEA/D算法[8]框架，候选解评价则是基于EGO算法[9]中的预测模型DACE模型[10](高斯随机过程模型)来评价候选解. 所以，针对MOEA/D和EGO算法，其并行化分析如下：

1)在EGO算法中，用高斯随机过程建立DACE模型的过程，每个目标都需要建立一个DACE预测模型，而在建模过程中，需要涉及到大量的矩阵运算，通过MOEA/D-EGO时间测试表4-5所示，每次建模都需要花费大量时间. 而在建模过程中每个目标的预测模型都是相互独立的，不难看出，在建模这个层次上，可以将每个目标的模型用分别在不同的进程中创建，最后将待评价的候选解分别在两个不同的进程中评价，最后交由主进程完成综合评价.

2)种群更新阶段，在定位候选解中完成. 需要执行种群个体杂交，变异操作，和更新邻居子问题表. 一方面，在这个过程中，因单个个体评估时间消耗大，而且种群数规模庞大，迭代次数较多. 所以时间开销大. 另一方面，每个个体的变异，更新都是相对独立的，更新操作只与其邻居个体有关. 所以我们可以将种群分布为几个子种群，每个子种群单独优化. 为此我们同样设计主从式模型，由于种群中的个体优化需要依赖其邻居子问题，所以我们需在每个进程上分布整个种群，每个进程只优化更新整个种群中自己所需演化的子种群中个体，子进程完成自己的任务后将优化后的种群个体发送给主进程.

2 并行MOEA/D-EGO算法实现

2.1 算法基本流程

算法的框架与实现如图1.

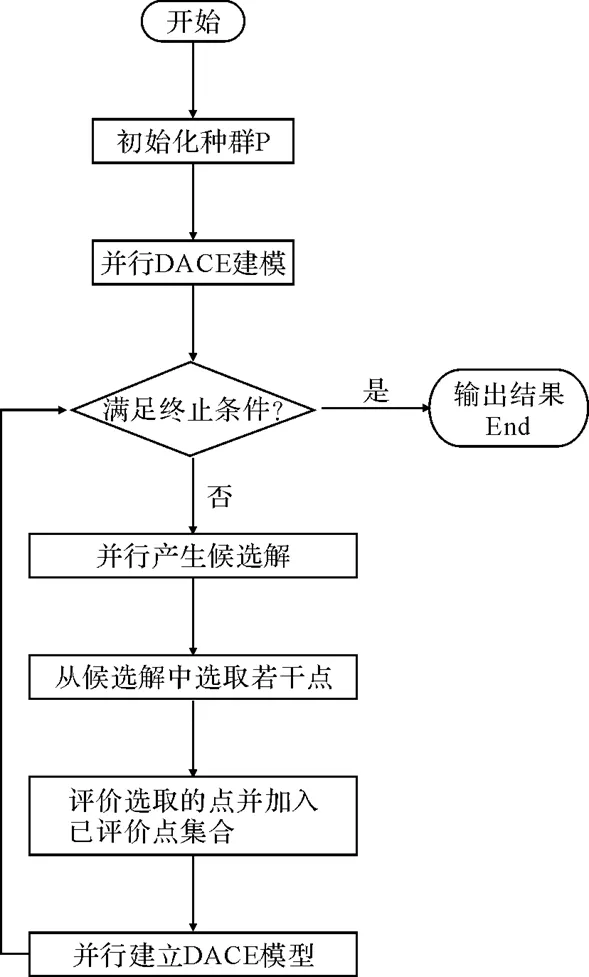
图1 MOEA/D-EGO算法流程

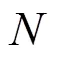
算法参数：

具体步骤：

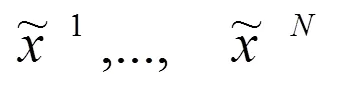
2.2 DACE建模并行化

目前，一般的单台机器大多数机器为双核，而同一台机器上的并行在数据发送，接收和节点控制上所消耗的计算机资源很少，并且Master上的Salve并不需要发送接收数据. 所以可以改进主从式并行模型[13]，我们使Master的节点同时也是Salve节点. 当MOEA/D-EGO的目标数比较少时，这种设置能够得到比较优良的结果. 模型图如2所示：

根据第1章的DACE预测模型并行化分析和图2的并行模型的设计，主进程和子进程的流程如下：

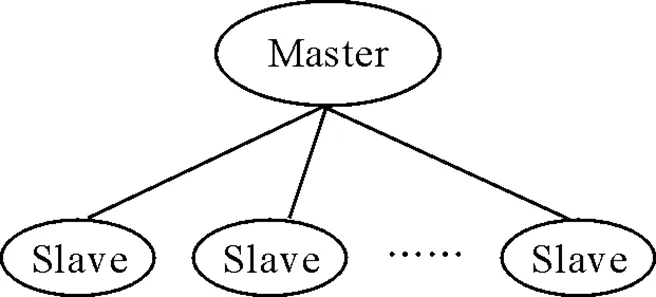
图2 多核并行模型

2.2.1主进程与子进程执行流程

上节已经对建立DACE预测模型的并行性做了分析，该模块基于主从式并行. 将每个目标的DACE预测建模设置在Master节点和不同的Salve节点上，并在不同的处理器核上运行. 由Mater将建模参数传送到Salve节点，Salve节点完成建模后，将模型传送给Master节点. 主要流程如下：

主进程：1)顺序执行到DACE建模阶段；2)主进将多个DACE建模的消息平均分布到子进程和主进程上；3)主进程完成自己所获的DACE预测模型建模；4)主进程接收子进程提交的建模模型信息并对信息进行加工处理，还原为DACE预测模型；5)主进继续执行，结束各个子进程.

子进程：1)顺序执行到DACE建模阶段；等待主进程发送建模所需参数；2)接收建模所需信息，完成DACE预测模型建模；3)将完成的DACE预测模型参数发送给主进程；4)子进程结束.

2.2.2并行DACE建模实现

1)将已评价的样本点变量值与适应值，进行封装；2)判断每个进程上所需建立的模型；3)主进程将1中封装的信息按照2的判断发送到相应的子进程；4)子进程利用3中的信息建模；5)子进程将4中得到的DACE预测模型的参数封装，发送给主进程；6)主进程将5子进程得到的信息还原为DACE预测模型；7)子进程结束，主进程继续执行.

2.3 种群优化并行化

在单机多核环境中，设置主进程运行在Mater节点上，主进程除了需要负责对各个Salve节点的控制，信息收发，信息收集和信息整合外，同时也需要演化分布在Mater节点上的子种群个体. Salve节点运行子进程，子进程完成子种群个体杂交变异，和更新个体邻居子问题表操作.

在第1章节中，已经对种群优化的并行性做了分析，该模块的并行基于主从式并行. 本论文中，由于实验条件限制，同样采用第二种方式. 即单机多核环境，将需要演化的子种群平均分配到CPU的每个核上，Master节点运行的主进程负责对节点的信息收发，控制，并且需要演化分布在自己节点上的子种群. Salve节点上的子进程负责演化分布其上的子种群，主要流程如图3.

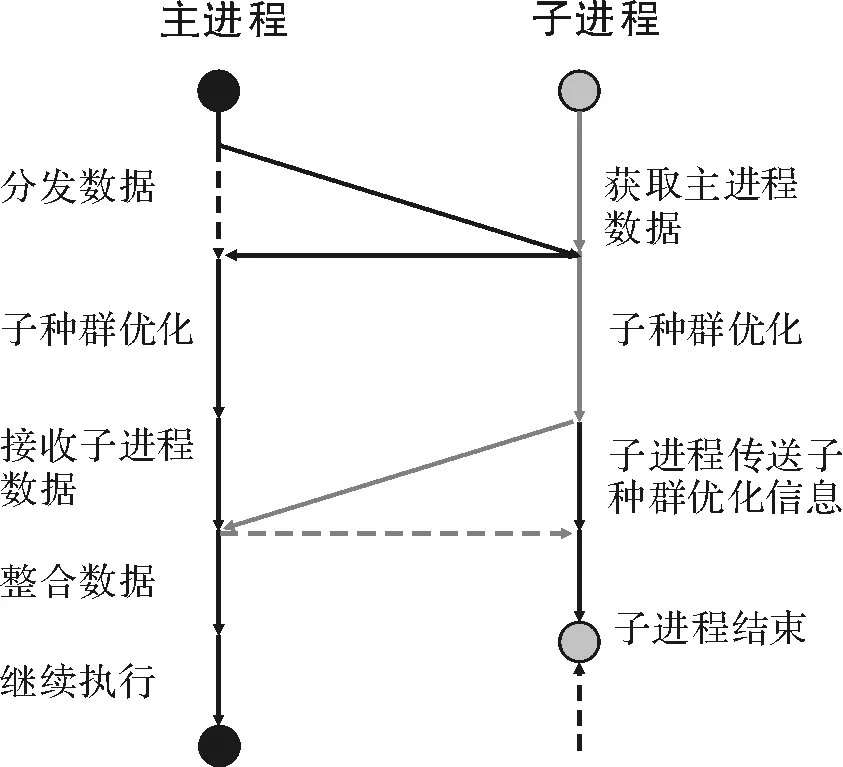
图3 并行种群优化流程示意图

3 并行MOEA/D-EGO结果分析

3.1 测试环境与参数设置

采取C++语言进行编写，开发软件为eclipse CDT，编译环境gcc version 4.4.0，并行环境是MPI，采用的并行库是MPICH，硬件上使用8核CPU的机器测试算法的并行.

表1(a) 算法性能测试硬件环境

硬件CPU内存硬盘 型号Inter (R) Core(TM)i7930@2.80GHz6 GB DDR2 800MHz500GB 7200RPM

表1(b) 算法性能测试软件环境

表2 测试函数集

3.2 算法运行结果记录与分析

为了验证并行MOEA/D-EGO算法的正确性，下面以2个目标函数的多目标问题ZDT1、ZDT3、ZDT6运行结果图和3个目标函数的的DTLZ2[11]运行结果图来说明. 图4至图7为算法在8核CPU的计算机环境中，种群大小为300个个体，评价次数为200的条件下，2个进程运行，取10次结果中的最优值. 图7为算法在8核CPU计算机环境中，种群大小为595个个体，评价次数为300的条件下，3个进程运行，取10次结果中的最优值.

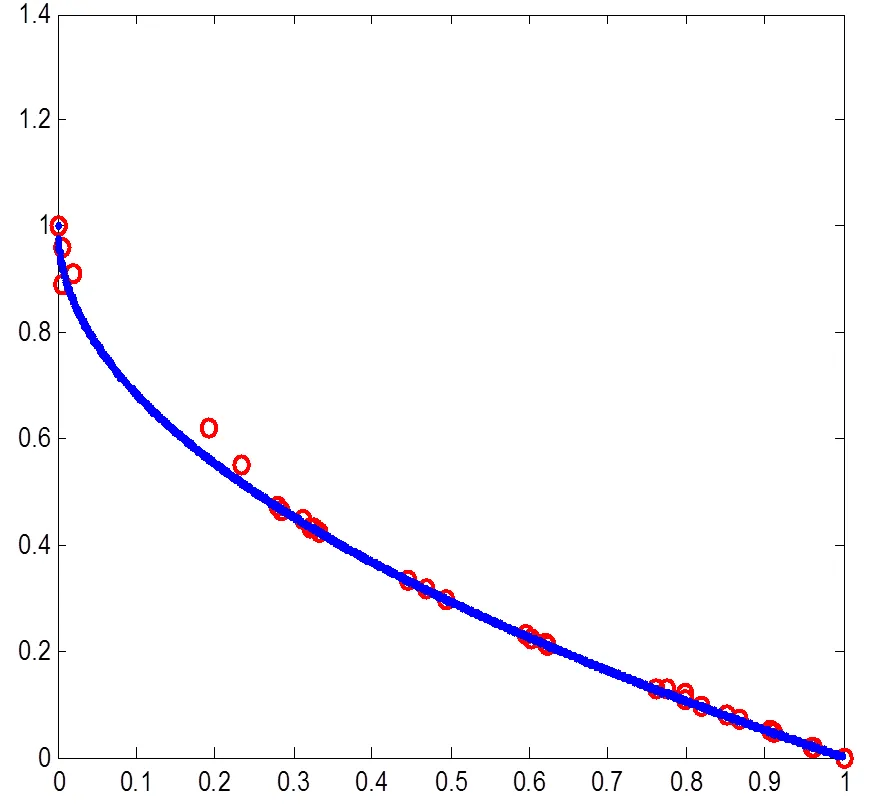
图4 ZDT1 8核2进程运行结果

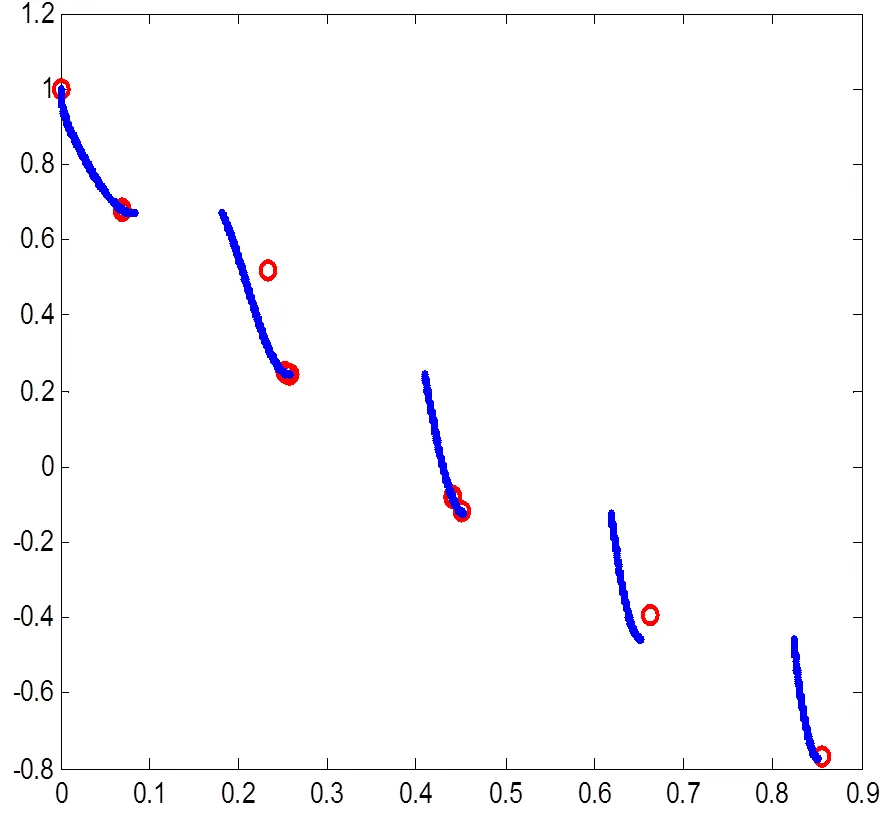
图5 ZDT3 8核2进程运行结果

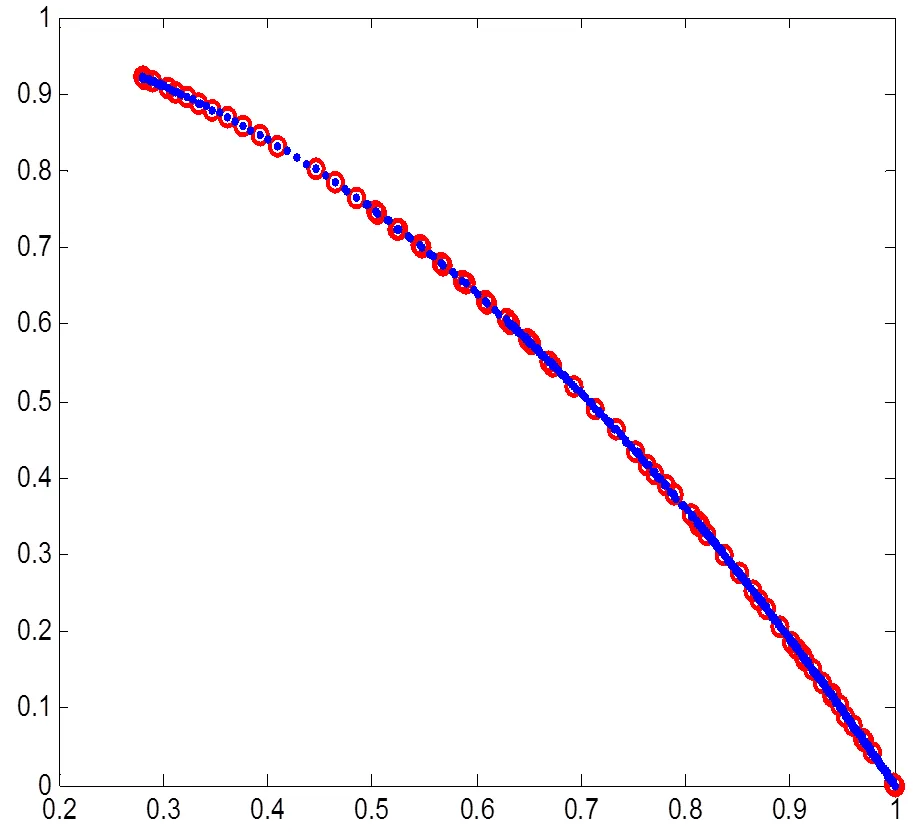
图6 ZDT6 8核2进程运行结果

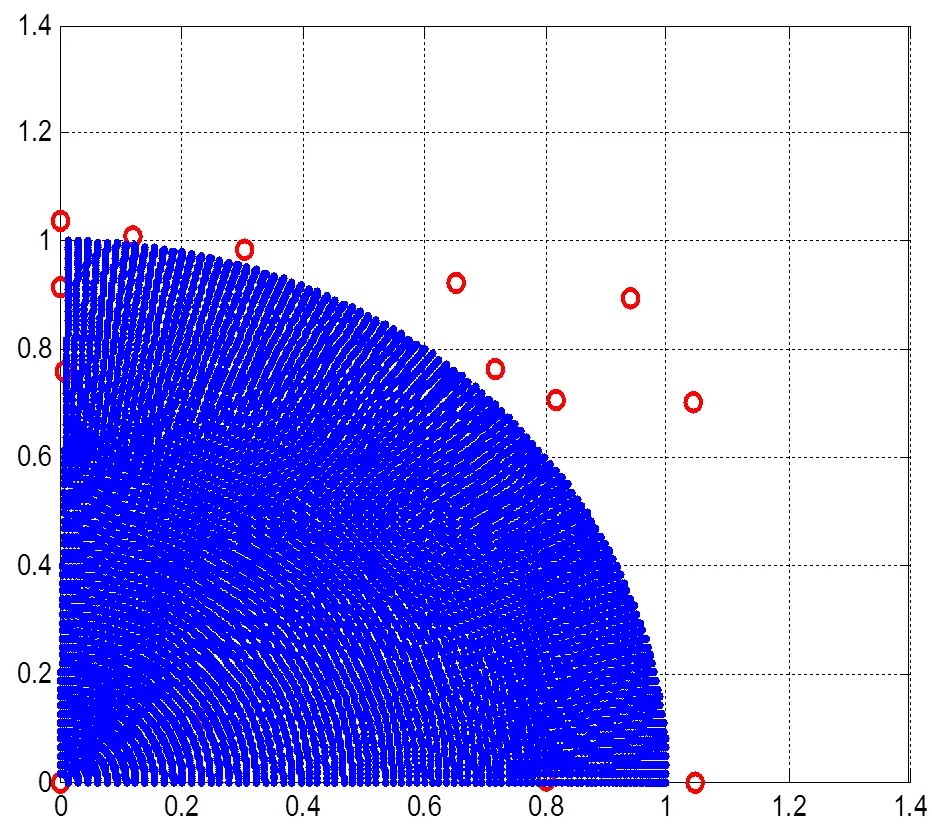
图7 DTLZ2 8核3进程运行结果

如图4至图7所示，算法在运行2个目标和3个目标的的经典测试函数时，能够得到较优的结果. 该结果验证了并行MOEA/D-EGO算法在有限评价次数之内能够得到测试问题的非支配收敛解，尽管收敛精度不能达到一般算法理论研究时的苛刻精度，但种群的非支配收敛趋势表明了算法在解决昂贵评价多目标问题上的正确性，以及算法具备实际应用能力.

为了研究并行MOEA/D-EGO算法在DACE建模过程中时间的节省，用1到8个进程执行了测试函数ZDT1. 如表3所示，测试函数40次运行过程中DACE建模时间对比，1-8个进程平均每次测试运行5次，建模时间为5次建模的平均值.

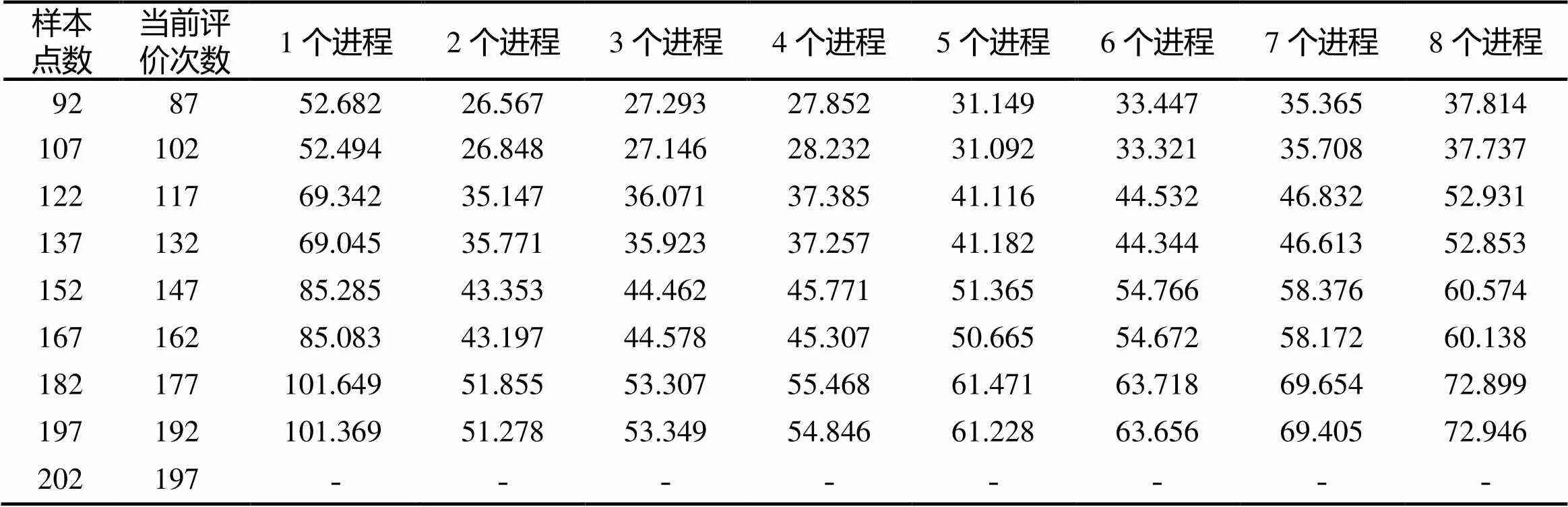
表3 8核环境多进程并行DACE建模时间对比(ZDT1测试) 单位: s

并行计算在建立DACE预测模型的过程中，因程序在建模级上作得并行即将每个模型的建立分配到不同的进程中，程序没有做粒度更小的并行，故在进程数超过目标数时，建模时间不会继续缩短，反而会因为进程的增多，计算机资源消耗增大而导致建模的时间相对增加.

为了研究并行MOEA/D-EGO算法在种群过程节省时间，采用1~8个进程执行了测试函数ZDT1. 表4所示，测试函数40次运行过程中种群优化过程花费的时间对比，1~8个进程平均每次测试运行5次，种群优化时间为程序5次运行的平均值.

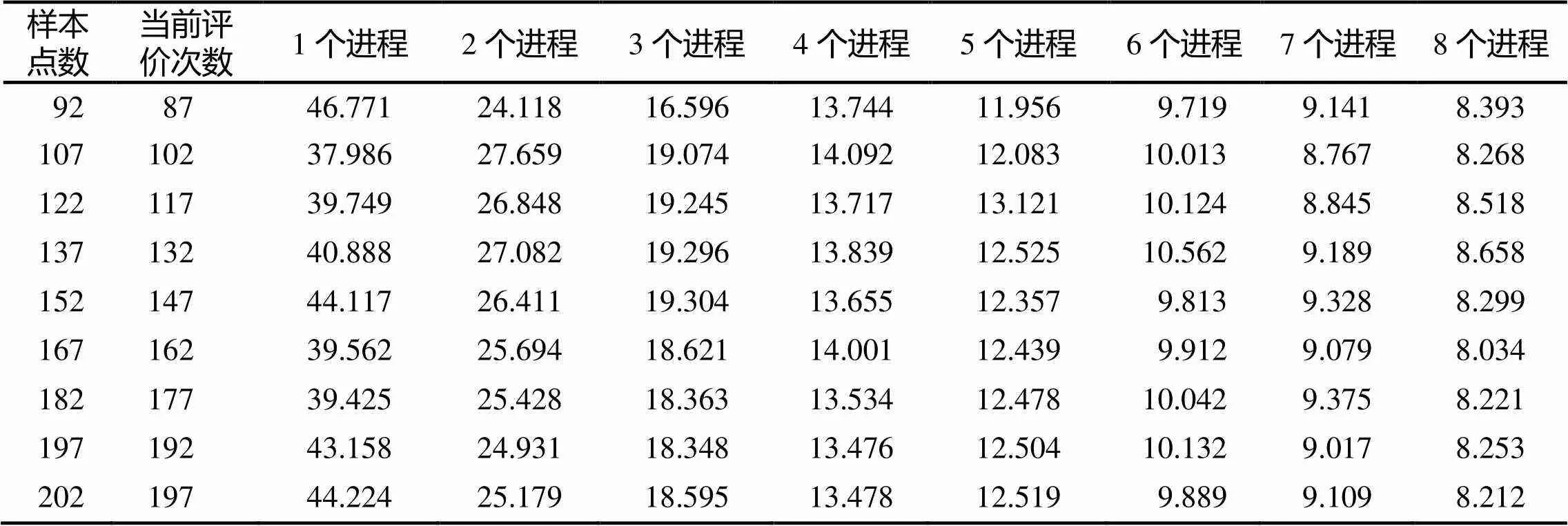
表4 8核环境多进程并行定位候选解时间对比 单位: s

并行计算在种群优化过程中，将种群的优化分布到多个进程中需要消耗一定的时间，所以在进程数继续增加过程中，种群优化过程时间的减少量的相对值变化会慢慢的减小，在实际应用中运行并行程序需要具体考虑进程数的安排个数.

为了进一步研究并行MOEA/D-EGO算法，如表5所示，算法在8核环境下，平均每次测试结果为3次程序的运行得出时间的平均值. 测试函数为2个目标的多目标函数种群大小为300，评价次数为200次；测试函数为3个目标的多目标函数种群大小为595，评价次数为300次. 为了更加清晰的现实算法的效率，本文给出了多进程运行的加速比，如表6所示.

表5 8核环境算法运行总时间对比 时间：s

表6 加速比对

通过表5所示程序运行时间对比与表6所示的加速比分析，很容易的看出当测试函数目标数为2，种群数为300，评价次数为200次的情况下，并行MOEA/D-EGO算法在进程数为3或4的时候效率最高，当进程数增加到8时候能够很明显的看出程序运行时间反而增大；当测试函数目标数为3，种群数为595，评价次数为300次的情况下，并行MOEA/D-EGO算法随着进程数的增加而运行时间减少，在进程数为8的情况下算法效率最高.

4 结语

本文围绕并行MOEA/D-EGO算法，对MOEA/D-EGO算法中的DACE建模过程和种群优化过程进行了并行性分析，采用基于主从式模型模型，实现了DACE建模的并行化和种群优化过程的并行化. 通过多个经典的测试函数的测试，实验结果不仅证明了算法能够有效解决昂贵评价多目标优化问题，而且验证了并行计算的利用能够使得MOEA/D-EGO算法在运行时间上获得较大负幅度的加速，对计算机资源的利用率有着显著的提高.

[1] ZHANG QINGFU, LIU WUDONG, TSANG E, et al. Expensive multiobjective optimization by MOEA/D with Gaussian process model[J]. IEEE Transactions on Evolutionary Computation, 2010, 14(3): 456-474.

[2] 陈国良. 并行算法的设计与分析[M]. 2版. 北京: 高等教育出版社, 2002.

[3] LOGOFĂTU DONIA, GRUBER MANFRED, DUMITRESCU D D. Distributed Evolutionary Algorithm Using the MapReduce Paradigm–A Case Study for Data Compaction Problem[M]. Berlin: Springer Berlin Heidelberg, 2011: 279-291.

[4] 李建江, 崔 健, 王 聃, 等. MapReduce并行编程模型研究综述[J]. 电子学报, 2012, 39(11): 2635-2642.

[5] 刘小明, 李 晖, 熊慕舟. 并行演化算法在MEMS继电器参数优化中的应用[J]. 计算机工程与应用, 2014, 50(6): 200-204.

[6] RYU SI-JUNG, KIM JONG-HWAN. Distributed Multiobjective Quantum-Inspired Evolutionary Algorithm[J]. Robot Intelligence Technology and Applications, 2013, 208: 663-670.

[7] JIN Y. A comprehensive survey of fitness approximation in evolutionary computation[J]. Soft Computing, 2005, 9(1): 3-12.

[8] ZHANG QINGFU, LI HUI. MOEA/D: A multiobjective evolutionary algorithm based on decomposition[J]. IEEE Transactions on Evolutionary Computation, 2007, 11(6): 712–731.

[9] JEONG SHINKYU, OBAYASHI SHIGERU. Efficient Global Optimization (EGO) for Multi-objective Problem and Data Mining[C]// IEEE. Proceedings of the 2005 IEEE Congress on Evolutionary Computation. Chicago: IEEE, 2005: 2138-2145.

[10] ULMER H, STREICHERT F, ZELL A. Evolution strategies assisted by Gaussian processes with improved pre-selection criterion[C]// IEEE. Proceedings of the 2005 IEEE Congress on Evolutionary Computation. IEEE, 2003: 692-699.

[11] DEB K, THIELE L, LAUMANNS M, et al. Scalable multi-objective optimization test problems[C]// IEEE. Proceedings of the 2002 IEEE Congress on Evolutionary Computation. Honolulu: IEEE, 2002: 825-830.

Parallel Computing in MOEA/D-EGO Algorithm

MA Yongge1,2, WU Zhao1

(1. College of Mathematical and Computer Sciences, Hubei University of Arts and Sciences, Xiangyang 441053, China; 2.School of Computer Science and Technology, China University of Geosciences, Wuhan 430074, China)

In MOEA/D-EGO algorithm, when there are too many modeling sample set elements or the population scale is large , it will lead to a long computation time. In order to reduce the run time of the MOEA/D-EGO algorithm, this paper parallelizes both the modeling process and the population optimization process. considering the experimental conditions, this paper uses the master-slave parallel model which adds the task to the main process in the condition of fully considering the efficiency of computer resources and load balance. The main process not only assigns computation task, distributes data, configures algorithm, collects the computation results, but also participates in the task of child process and complete the same amount of computation task as child process. The experimental result shows that the paralleled MOEA/D-EGO algorithm can effectively solve the multi-objective optimization problem, and can significantly shorten the running time of the algorithm.

MOEA/D-EGO algorithm; Parallel computing; Candidate solution; Population optimization

TP301.6

A

2095-4476(2014)05-0009-06

2014-03-03;

2014-04-01

国家自然科学基金重点项目(31130055); 国家自然科学基金面上项目(31372573, 61172084); 湖北省自然科学基金项目(2013CFC026); 湖北省科技支撑计划项目(2013BHE022)

马永格(1987— ), 女, 河北藁城人, 湖北文理学院与中国地质大学(武汉)联合培养硕士研究生;

吴 钊(1973— ), 男, 湖北武汉人, 湖北文理学院数学与计算机科学学院副教授, 博士, 中国地质大学(武汉)兼职硕士生导师，主要研究方向: 智能算法, 云计算.

(责任编辑：饶 超)