二维网格上经纪人模仿引起的自组织分离与聚合
杨伟松,杨德军
二维网格上经纪人模仿引起的自组织分离与聚合
杨伟松1,杨德军2
(1. 江西科技师范大学 通信与电子学院,江西 南昌 330013;2. 湖北文理学院 教育学院,湖北 襄阳 441053)
将“演化的争当少数者博弈”模型(EMG)建立在41×41的二维正方形网格上,格点代表经纪人,连线代表该两相邻经纪人存在联系,每个经纪人被随机分配一个介于0与1之间的基因策略值。数值模拟结果表明:模型的奖惩比等于或大于1时,随着演化过程的进行,系统经纪人倾向于模仿具有极端基因策略值(接近0或1)经纪人的策略,说明极端的决定策略比犹豫策略(接近0.5)的表现要好,能使经纪人获得更大收益;当经纪人策略自组织分离现象出现后,人群-反人群效应更加明显,系统一方人数的变化偏差显著降低,系统资源得到更加有效的利用. 而当模型的奖惩比小于1时,即处于困难时期时,中间犹豫策略的表现则比极端策略要好.
EMG模型;二维网格;经纪人模仿;人群-反人群效应;自组织分离与聚合
从MG及EMG模型提出以来,有许多研究者在其基础上做了些引入模仿的工作. 如Slanina研究了一维周期链结构中的模仿少数者博弈模型[1-2],Quan等人研究了模仿合金少数者博弈模型[3]及双向模仿的演化少数者博弈模型[4]. 他们发现经纪人分布在一维周期链上通过相邻经纪人的策略模仿会提高模型系统的整体效率.
本文假设将EMG模型的经纪人放在二维网格上,考察通过相邻经纪人之间的模仿以及在不同的环境奖惩比条件下系统中经纪人的策略分布变化状况以及系统整体效率的演化情况.
1 演化模型
在D. Challet等人提出“争当少数者博弈”模型(MG叫做)[5-6]的基础上,N. F. Johnson等人提出了一种“演化的争当少数者博弈”模型(EMG)[7]. 模型如下:
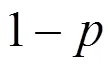
本文假设经纪人分布在一个41×41的二维正方形网格上,每个格点代表一个经纪人,连线代表该两相邻经纪人存在联系. 这样除了边界线上的格点之外,每个格点一共有上下左右四个邻居.
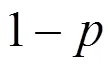
2 数值模拟
根据模型设定规则,用FORTRAN语言编程计算策略分别在从0到1的10个小区间(区间长度为0.1)内的经纪人数目,并用Origin软件画图. 开始时系统经纪人的策略分布情况见图1,经过一段时期(10000000时步)的演化后,系统中经纪人的基因策略值出现自组织分离现象,结果见图2.
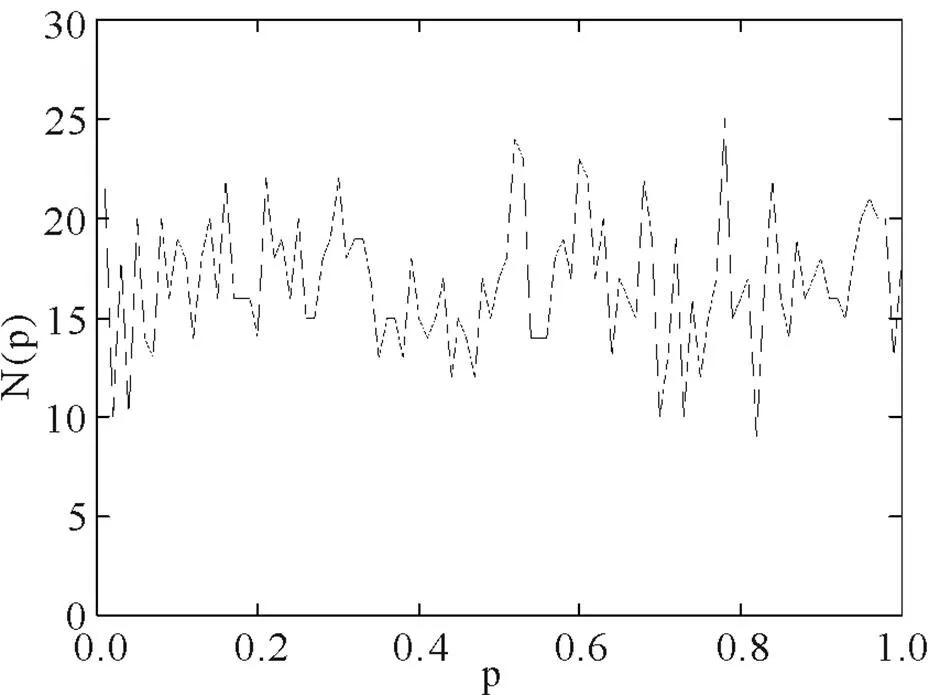
图1 开始时系统中经纪人的基因策略分布
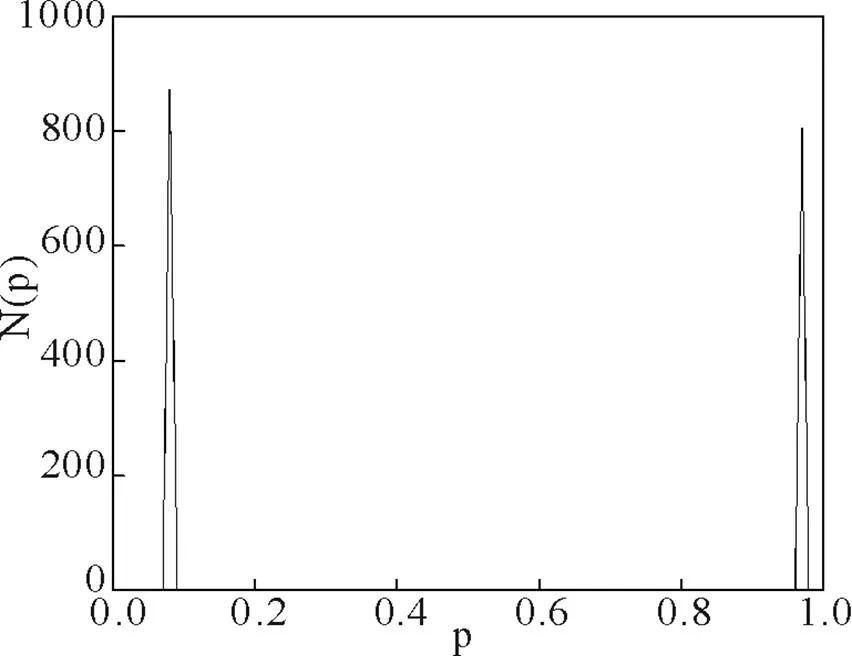
图2 经过10000000时步演化后系统中经纪人的基因策略分布
从图1和图2的结果来看,经过10000000时间的演化后,经纪人倾向于拥有两个极端策略中的一个,在策略自组织分离现象出现后,会形成典型的人群-反人群效应,从而有效降低系统某方人数的变化方差,这意味着少数方或获胜方的人数会增加,更多的人会享受到利益,从而提高系统整体资源的利用效率.
此外,以1000时步为一代,让系统运行10000代,并统计了每一代中系统一方人数的波动标准偏差,标准偏差的定义如下:
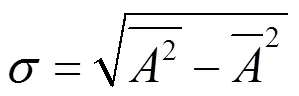
系统标准偏差随演化代数的变化关系见图3.
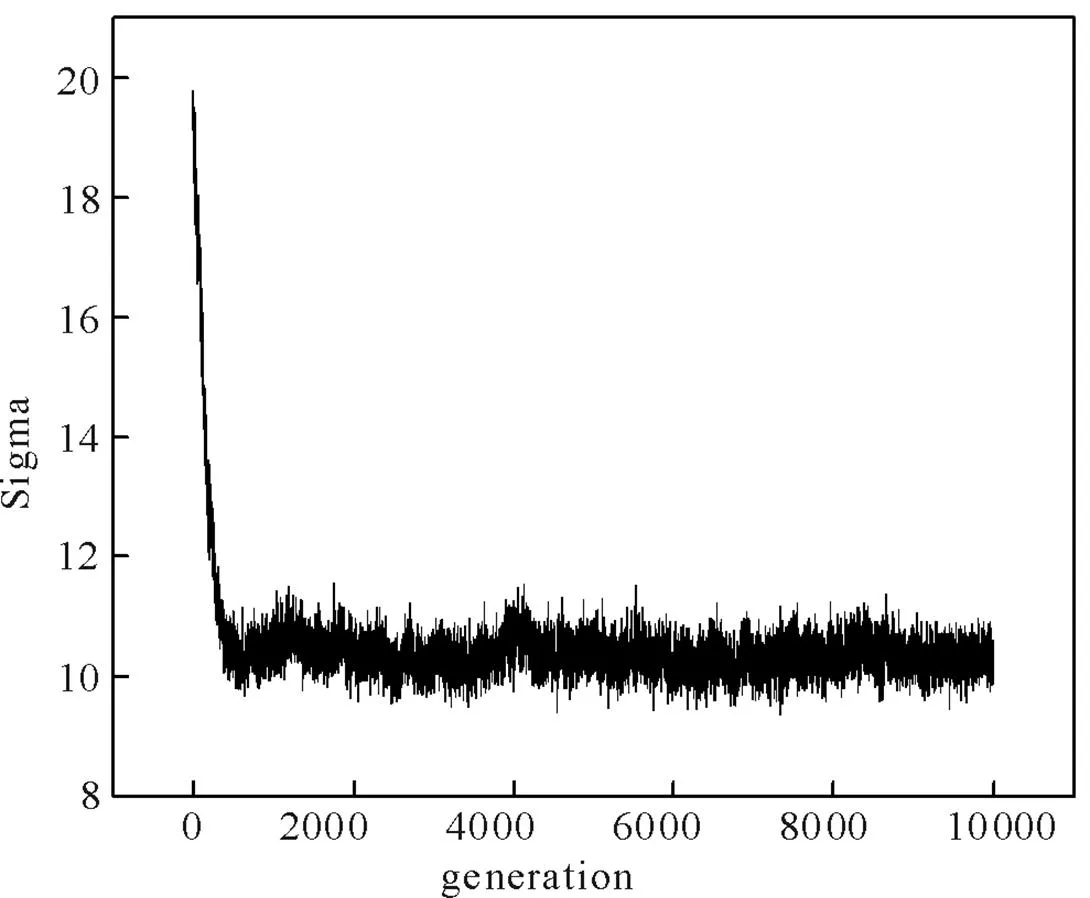
图3 系统一方人数的波动标准偏差随演化代数的变化关系
当假设模型系统的奖惩比小于1时,即设经纪人进入少数方获得的奖励为0.8分,进入多数方得到的惩罚为1分时,数值模拟计算发现,经过一段时期(10000000时步)的模仿演化后,系统中经纪人的基因策略值会出现与自组织分离相反的现象,即趋向集中于采用中间策略.
进一步考虑奖惩比情况更强烈的情况:如奖惩比更大如1.2时,模型系统经过长时期(10000000时步)演化后,经纪人策略分布状况与奖惩比等于1的模型系统的情况类似;当奖惩比更小如0.6时,模型系统经过长时期(10000000时步)演化后,经纪人策略分布状况则与奖惩比等于0.8的模型系统的情况类似. 说明安乐时期(奖惩比大于等于1)与困难时期(奖惩比小于1)系统经纪人的优势策略存在本质的区别.
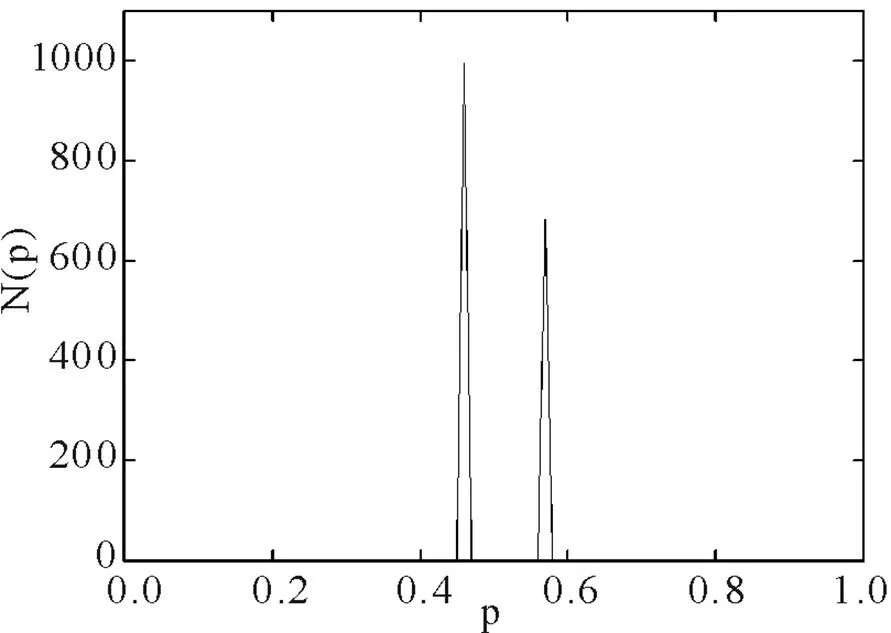
图4 奖惩比为0.8时经过10000000时步演化后系统中经纪人的基因策略分布
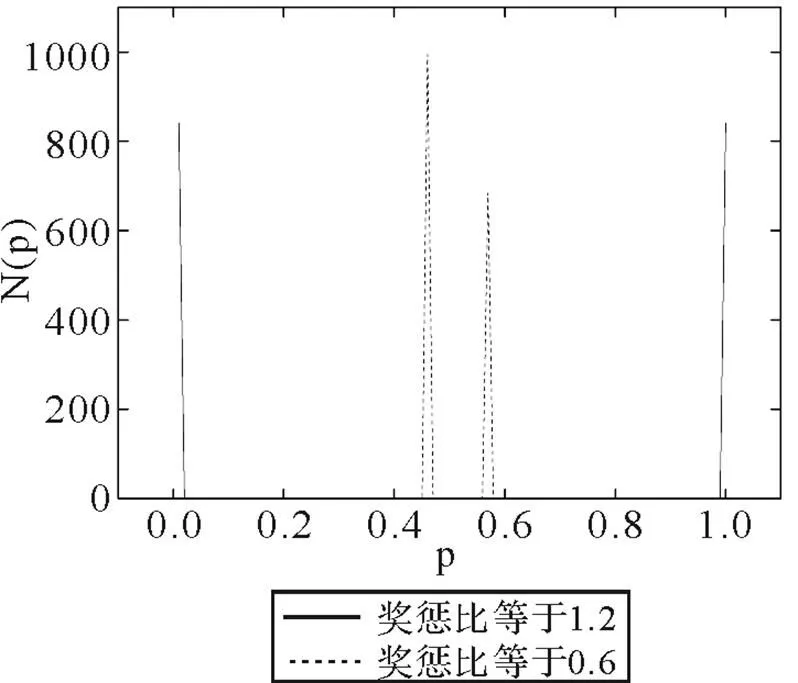
图5 奖惩比分别为1.2和0.6时经过10000000时步演化后系统中系统中经纪人的基因策略分布
3 讨论
文章数值模拟的时步比传统模型要长,结果也更可靠. 从数值模拟结果来看,当模型的奖惩比等于或大于1时,随着演化过程的进行,系统经纪人倾向于模仿具有极端基因策略值(接近0或1)经纪人的策略,说明极端的决定策略比犹豫策略(接近0.5)的表现要好,能使经纪人获得更大收益. 当经纪人策略自组织分离现象出现后,人群-反人群效应更加明显,系统一方人数的变化偏差显著降低,系统资源得到更加有效的利用. 而当模型的奖惩比小于1时,即处于困难时期时,中间犹豫策略的表现则比极端策略要好.
[1] SLANINA FRANTIŠEK. Social organization in the minority game model[J]. Physica A: Statistical Mechanics and its Applications, 2000, 286(1-2): 367-376.
[2] SLANINA FRANTIŠEK. Harms and benefits from social imitation [J]. Physica A: Statistical Mechanics and its Applications, 2001, 299(8-10): 334-343.
[3] QUAN HONGJUN, WANG BINGHONG, HUI PAK-MING, et al. Cooperation in the mixed population minority game with imitaiton[J]. Chinese Phys. Lett., 2001, 18(9):1156-1158.
[4] QUAN HONGJUN, WANG BINGHONG, HUI PAK-MING. Effects of imitation in a competing and evolving population[J]. Physica A: Statistical Mechanics and its Applications, 2002, 312(3-4): 619-626.
[5] CHALLET D, ZHANG Y C. Emergence of cooperation and organization in an evolutionary game[J]. Physica A: Statistical Mechanics and its Applications, 1997, 246(3-4): 407-418.
[6] CHALLET D, ZHANG Y C. On the minority game: Analytical and numerical studies[J]. Physica A: Statistical Mechanics and its Applications, 1998, 256: 514-532.
[7] JOHNSON NEIL F, HUI PAK MING, JONSON ROB, et al. Self-organized segregation within an evolving population[J]. Phys. Rev. Lett., 1999, 82: 3360-3363.
Self-segregation and Clustering Induced by Agents’ Imitation on Two-dimensional Lattice
YANG Weisong1, YANG Dejun2
(1. College of Communication and Electronics, Jiangxi Science & Technology Normal University, Nanchang 330013, China; 2.College of Education, Hubei University of Arts and Science, Xiangyang 441053, China )
With EMG model on 41×41 two-dimensional lattice, lattice point represents agent, ligature represents communication of two neighbouring agents, and each agent is assigned a gene strategy p value between 0 and 1 randomly. Numerical simulation shows that when prize-fine ratio of model is equal to or larger than 1, with proceeding of evolution, agents in system tend to imitate the strategy of agents who have extreme gene strategy(near 0 or 1), which shows extreme strategy performs better than hesitate strategy(near 0.5), and may brings more benefit to agents; when self-segregation phenomenon of agent strategy appears, crowd-anticrowd effect is more evident, the variance of the number of agents in one side reduces significantly, the system resource is utilized more efficiently. When the prize-fine ratio is less than 1, namely in difficult period, middle hesitate strategy performs better than the extreme strategy.
EMG model; Two-dimensional lattice; Agent imitation; Crowd-anticrowd effect; Self-segregation and clustering
O225
A
2095-4476(2014)05-0021-03
2013-12-05;
2014-03-20
杨伟松(1977— ), 男, 江西南昌人, 江西科技师范大学通信与电子学院讲师.
(责任编辑:饶 超)

