基于光折射定律的虹成因分析及其应用

郑其明

(南京化工职业技术学院，江苏南京 210048)

0 引言

彩虹是常见的自然现象，常在夏日的雨后发生。对于彩虹形成的原因，早在十七世纪时，法国物理学家Rene Descartes就已经用几何光学的原理分析过［1］，此后物理学家通过波动光学和微分方程对彩虹原理解释得更加精确［2］，但这些解释对普通大学生而言很难理解。本文在基于光的折射定律的基础上［3］，通过理论和实验两个角度，利用简单的数学方法，对彩虹形成原因进行了解释，让学生更直观地了解彩虹形成的原因，进而利用本文提出的原理，发展出一种测量液体折射率的新方法。

1 虹形成原因的理论分析

虹的形成是由于光线射入空气中的小水滴，经另一侧内反射后，光线从同一侧面折射出来，从而观察到虹。由于阳光(白色光)是由7种单色光组成，不同单色光对水的折射率不同，白色光经过水滴折射后，折射光线会分解成不同单色光，因此观察到的虹是彩色的。最容易被观察到的彩虹是经过水滴一次内反射后形成的，其观察角往往在与水平面成α=42°角处［4］(即彩虹形成的观察最大角度)。在适当的条件下肉眼也可以看到经过多次内反射后形成的高阶彩虹。由于高阶彩虹形成原理比较复杂，本文只研究单阶彩虹的情况。

在一般教材或相关资料中都会介绍到彩虹与水平面形成42°的角，但一般并不说明形成42°的角的原因和其物理意义，本文从理论和实验两个角度对此问题进行分析。

图1 彩虹形成原理的光路示意图

考虑一道单色光在小水滴内单次内反射的情形，如图1所示，θ为入射角，φ为折射角，光线经过水滴内反射和折射后的偏折角是入射角θ的函数，并随着入射角的变化而变化，记作A(θ)。由图可知，出射光线与水平线的夹角为α。有:

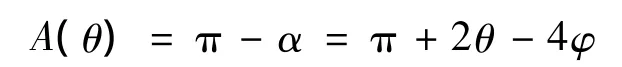
根据光的折射定律，设空气的折射率为n，可得，sin θ=nsin φ，代入上式得:

同时由图1可知，入射光线(或其延长线)到水滴中心宽度:h=Rsin θ，h随着入射角θ的变化而变化，对具体小水滴而言，其半径为常数，则有:

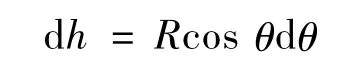
而A(θ)是关于 θ的函数，故有:对θ的导数即为A(θ)函数曲线上任意一点的斜率。所以，代入 dh=Rcos θdθ，可得:

由以上分析和式(2)可知，对一小段偏折出来的光线dA(θ)而言，所得到的入射光线的宽度越大，出射光线就越明亮，越容易通过肉眼观察到。当dh/dA(θ)取最大值时，即A'(θ)为极小值时，出射光线将会最强。

对函数关系式(1)求极值，取光对水的折射率为n=1.333，以 θ为横坐标，A(θ)为纵坐标，由数学软件可得到如下函数图像［5］(如图2所示)。并由图像2可得，A(θ)可取极小值138°，因此虹最大观察角 αmax=π－A(θ)=42°。当然不同的单色光折射率不同，形成虹时其最大观察角也不同，白色光形成虹时，各种单色光被分解开来，因此由阳光形成的虹是彩色的。

3 虹形成原因的实验验证

以上理论分析的结果可以通过实验进行验证。如图3所示，取一个薄的圆柱形玻璃管注满水，让一束激光从玻璃管的一侧射入，从玻璃管的同侧和另一侧都会有光线折射出来，改变入射光的角度，观察从玻璃管的两侧折射出来的光线的角度和强度的变化。

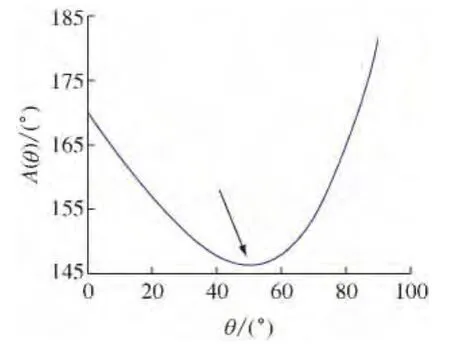
图2 偏折角与入射角的函数关系图像

由实验观察的现象可知，当入射光的角度发生变化时，从两侧折射出来光线角度和强度都会产生变化。当从同侧折射出来的光线与水平面夹角为最大时，这时从同侧折射出来的光线强度最强、宽度最窄，其折射光线将形成一束明亮的细光束(如图4(b)所示)，而在其他角度时，从同侧折射出来的光线较宽，亮度也较暗(如图4(a)所示)。本实验过程中使用是绿色激光，其相对于纯水的折射率为1.333，当从同侧折射出的光线与水平面夹角为42°左右时，出射光的宽度最窄、强度最强。由实验可以看出，当光线以不同角度入射时，经过水滴反射和折射后，从不同侧面折射出的光线的角度与强度都会产生变化，当从同侧面折射出来的光线与水平面夹角为最大角度时，折射出来的光线的宽度最窄、强度最大，在这个角度上也就最容易看到折射出来的光线。在其它角度上观察到的折射光线都比较弱，不容易观察到。当然对于彩虹的形成而言，当阳光照射向水滴时，在折射光线与水平面成42°角度方位上就容易观察到彩虹。若将本文实验中使用的绿色激光换成一束白色自然光，就可以模拟彩虹形成的现象。

图3 激光射入注满水的薄圆柱形玻璃管时的情形

4 利用虹形成原理测量液体的折射率

根据上面对虹形成的原因分析过程可以看出，当折射率不同时，从水滴中折射出来的光线与水平面最大夹角αmax也不同。如果能测量出从水滴中折射出来的光线与水平面最大夹角αmax，并得出最大夹角与液体折射率之间的关系，就可得到一种全新的测量折射率的方法。

图4 从圆柱体同侧折射出光线宽度与强度随出射光角度的变化

在上述分析中已经得出关系式(1)。又由图1可知:sin θ=h/R，设 sin θ=h/R=，其中R为水滴的半径。代入式(1)可得:

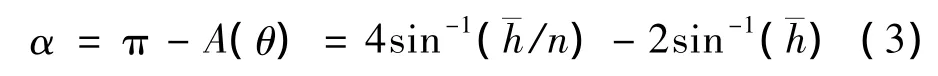
其中，n为液体的折射率，对于已知液体而言，其折射率为常数，α随着变化而变化。

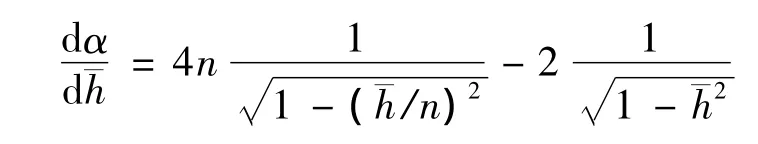
当dα/d=0时，α取最大值。当α取最大值时，由上式可得。代入式(3)得:

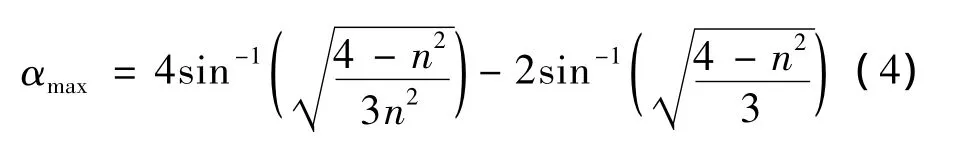
由式(4)可知，取不同的折射率为n的液体可得到不同的αmax，利用数学软件可绘制出(4)式的函数图像［5］，如图5所示，并可列出相应的数据表，如表1所示。

图5 αmax与折射率的函数关系

表1 αmax与折射率的数值关系

图5为αmax与折射率n的函数关系图。如果光束照射过某液滴的αmax可以被精确测量，那么由式(4)的关系式可推得出此液体的折射率n。由于图5应用在实际的测量上很不方便，于是为了方便由αmax的量测查出与其相对应的折射率n的值，利用图5的结果制作了表1。只要测量出某一液体的αmax，就可以利用表1查出此液体相对应的折射率n。与传统测量液体的折射率方法相比，利用此方法测量液体折射率有以下几个优点:

(1)由式(4)推导过程可知，该公式推导没有取近似，不存在系统误差，并且αmax与n具有严格一对一关系，因此只要测量一个参数αmax就能够计算出液体折射率，需要测量参数少，测量误差就小，测量结果的精度就高。

(2)参数αmax是光从水滴中折射时出来时，折射光线与水平面最大夹角，此时折射光线最窄、最强，容易通过视觉确定其位置，因此参数αmax比较容易准确测量。在条件许可时αmax容易实现自动测量，可以减少由于人为因素造成的误差。

(3)该测量所需要的仪器少，实验装置结构简单，一般实验室都能进行此测量。

(4)在进行测量时，既可以固定液体，测量不同单色光对同一种液体的折射率，又可以改变液体，测量同一种光对不同液体的折射率，测量方便易行。

在常温下，通过实验测得绿色激光对饱和食盐水的αmax值为35°，查所对应的折射率表，可以得到，绿光对饱和食盐水折射率:

与用其他方法测量的结果相比较，运用本文提出方法测量的结果的准确性更高。

同时由式(4)可知，αmax与水滴的半径无关，只与液体的折射率有关。在彩虹形成时，空气中小水滴的半径并不相同，但由于是同种液体，所有小水滴形成的αmax都约是42°，根据几何学原理，很容易证明出来所观察到的虹常常是圆弧形。只不过当水滴半径越大，观察到的虹越明亮。

5 结语

虹是一种常见的自然现象，但要从理论上对虹进行准确的解释是不容易的，本文从理论和实验两个角度解释了虹形成的原因，文中理论推导过程中使用的数学工具简单，避开了复杂的数学技巧，容易为普通大学生掌握和应用，本文的实验验证也容易在实验室开展，并且在理论和实验的基础上发展出更为精确的一种测量折射率的新方法。本文提出的方法对拓展学生知识面，引导学生运用物理学与数学原理对自然现象进行解释，提升学生运用知识的能力是十分有益的。同时本文提出的测量折射率的新方法，对液体折射率测量同样有着实际意义。

［1］Marion J B.Thornton S T.Classical Dynamics［M］.Harcourt Brace＆ Company，1995:217.

［2］John David Jackson，Classical Electrodynamics［M］.John Wiley ＆Sons，1999.

［3］姚启钧.光学教程［M］.4版.北京:高等教育出版社，2009.

［4］郁道银，谈恒英.工程光学［M］.北京:机械工业出版社，2003.

［5］张磊.MATLAB实用教程［M］.北京:人民邮电出版社，2008.

［6］Wolfgang G，Peter H.Interface analysis in biosensor design［J］.Biosensors＆ Bioelectronics，1995，10(9):853-883.

［7］郑其明.基于迈克尔逊干涉原理的反射式光电检测仪测量高分子材料的折射率［J］.安徽师范大学学报(自然科学版)，2012，35(1):32-34.

ZHENG Qi-ming.Measurements of Refractive Index of Polymer Materials Using Photoelectricity Reflectometry Based on Michelson Interference Method［J］.Journal of Anhui Normal University(Natural Science)，2012，35(1):32-34.

［8］同济大学数学系.高等数学［M］.上海:同济大学出版社，2009.

［9］吕斯骅，段家忯.新编基础物理实验［M］.北京:高等教育出版社，2006.

［10］沈元华，陆申龙.基础物理实验［M］.北京:高等教育出版社，2003.

［11］孙礼林，冯 松，李庆海，等.聚氧乙烯(PEO)、丙烯酰胺与甲基丙烯酸甲酯三元共聚物的合成与表征［J］.安徽师范大学学报(自然科学版)，2003，26(3):249-252.

SUN Li-lin，FENG Song，LI Qing-hai，SHEN Liang-jun.Synthsis and characterization of tri-copolymer poly(ethylene oxide)macromonomer acrylamide and methyl methacrylate［J］.Journal of Anhui Normal University(Natural Science)，2003，26(3):249-252.

［12］万新军，褚道葆，陈声培，等.不锈钢表面修饰纳米合金膜电极的电催化活性研究［J］.安徽师范大学学报(自然科学版)，2007，30(5):567-569.

WAN Xin-jun， CHU Dao-bao， CHEN Sheng-pei， et al.Electrocatalytic Activities of the Film Electrode Modified Nanocrystalline Alloy on the Stainless Steel［J］.Journal of Anhui Normal University(Natural Science)，2007，30(5):567-569.

［13］Tearney G J，Brezinski M E，Southern J F，et al.Determination of the refractive index of highly scattering human tissue by optical coherence tomography［J］.Appl Opt，1995，20(21):2258-2260.

［14］左则文.等厚干涉法测量薄膜厚度的两种方法［J］.安徽师范大学学报(自然科学版)，2012，35(1):32-34.

ZUO Ze-wen.Two Methods for Measuring the Thickness of Films Based on Equal Thickness Interference［J］.Journal of Anhui Normal University(Natural Science)，2012，35(1):32-34.

［15］房晓勇.固体物理学［M］.哈尔滨:哈尔滨工业大学出版社，2004.