基于遗传模拟退火算法的汽车动力总成悬置系统优化设计

严小俊，蒋伟康，曹 诚

（1．上海大众汽车有限公司，上海 201805；2．上海交通大学机械与动力工程学院，上海 200240）

基于遗传模拟退火算法的汽车动力总成悬置系统优化设计

严小俊1，2，蒋伟康2，曹 诚1

（1．上海大众汽车有限公司，上海 201805；2．上海交通大学机械与动力工程学院，上海 200240）

针对某轿车在发动机低速工况下，动力总成悬置系统隔振效果不足，以悬置系统的固有频率配置和系统的解耦率为综合优化目标，应用遗传模拟退火算法对悬置刚度参数进行了优化设计，优化后的悬置系统固有频率配置更加合理，主要方向的解耦率增大。整车试验结果表明，优化后的悬置系统隔振效果满足了设计要求。

动力总成；悬置系统；隔振；解耦；优化设计；遗传模拟退火算法

某紧凑型轿车在发动机低速工况下，动力总成悬置系统的隔振性能差，动力总成传递到车身的振动过大，降低了乘坐舒适性，需要对现有悬置系统进行优化设计从而提高产品质量。

本文使用遗传模拟退火优化算法，以悬置系统的固有频率配置和系统的解耦率为综合优化目标，以三个悬置的刚度为优化设计变量，对现有悬置系统进行优化设计，优化后的悬置系统装车后进行整车隔振性能试验，验证其在整车上的隔振效果，用振动传递率作为隔振效果的评价指标，要求振动传递率要大于20 dB［1］。

1 动力总成悬置系统试验

针对现有悬置系统隔振性能差的问题，本文先在整车上进行悬置系统隔振性能试验，通过得到的振动传递率定量评价现有悬置系统的隔振效果，从而发现问题。

试验时，在左悬置、右悬置和后悬置的主动端和被动端布置加速度传感器，用来采集发动机在整个转速范围内的加速度信号。

试验数据处理时需要得到振动传递率，传递率是指主动端加速度值与被动端加速度值的比值［1］。比值越大表示隔振效果越好。用分贝的形式表示为：

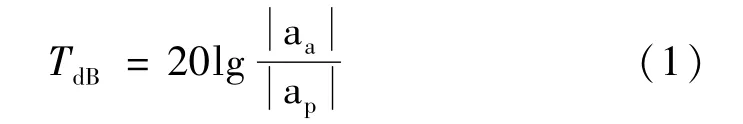
式中aa为悬置元件发动机侧的加速度，ap为悬置元件车身侧的加速度，用LMS Test-Lab处理试验数据时，只抽取在z方向的二阶振动加速度，得到三个悬置元件的振动传递率，如图1所示。

从图1中可以看出，右悬置和后悬置的传递率在各个工况中均大于20 dB，隔振效果较好，但左悬置在发动机低速段振动传递率小于20 dB，隔振效果有待改进。

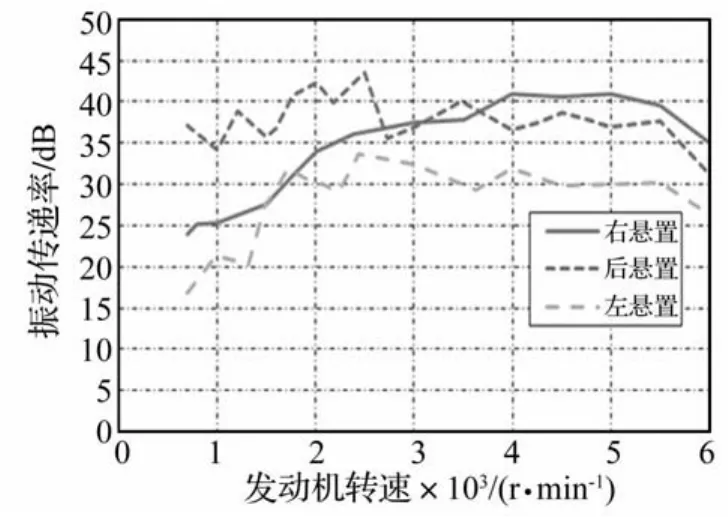
图1 悬置元件振动传递率Fig．1 Vibration transfer rate of engine mount

2 动力总成悬置系统的动力学模型

要提高悬置系统在整车上的隔振效果，需要对悬置系统本身进行优化设计，固有频率分配和解耦率是悬置系统的两个重要特性，要分析现有悬置系统的固有特性有哪些不足，首先需要建立悬置系统六自由度振动模型［2］，图2为悬置系统三维模型。

图2 悬置系统六自由度模型Fig．2 Powertrain mounting system six DOF model

图2中，坐标系Go-XYZ为定坐标系，原点Go位于动力总成质心处，X轴正方向与汽车的前进方向相反，Y轴与曲轴中心线重合，指向发动机前端，Z轴的正方向垂直于地面向上。坐标系G-xyz为动坐标系，静平衡时，动、定坐标系重合。动力总成的广义坐标为总成质心沿定坐标系X、Y、Z轴的x，y，z平移及绕X、Y、Z轴的转角θx，θy，θz，记为q＝［x，y，z，θx，θy，θz］T。

在分析悬置系统的固有特性时，不考虑系统的阻尼和外力作用，悬置系统的动力学方程［3］表达如下：

式中，M为悬置系统的质量矩阵，可由动力总成的质量和惯性参数得到，参数如表1所示。

表1 动力总成相对于质心坐标系的惯性参数Tab.1 Inertia parameter of powertrain mounting system

K为悬置系统的刚度矩阵，可由三个悬置元件的位置和刚度参数得到，参数如表2，表3和表4所示。

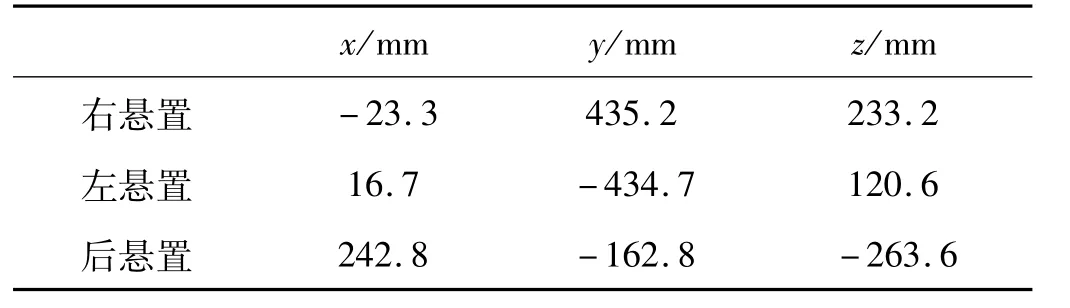
表2 动力总成悬置点相对质心位置坐标Tab.2 Coordinates of powertrain mounts position

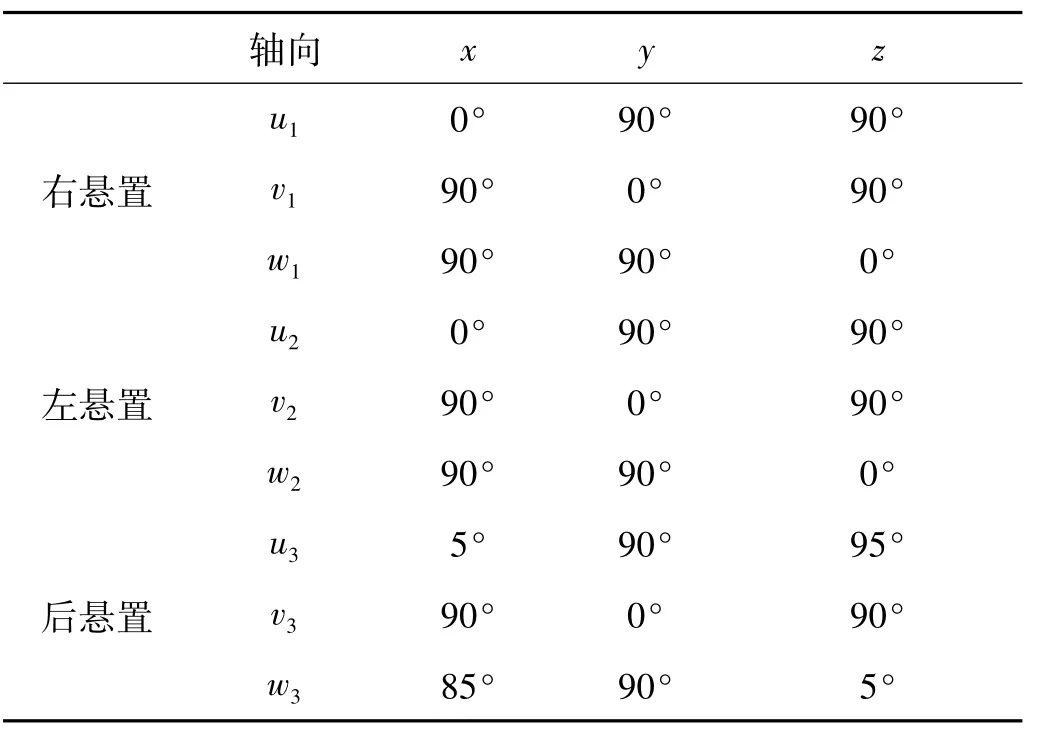
表3 悬置元件与广义坐标系的夹角Tab.3 Angles between powertrain mounts and the generalized coordinates

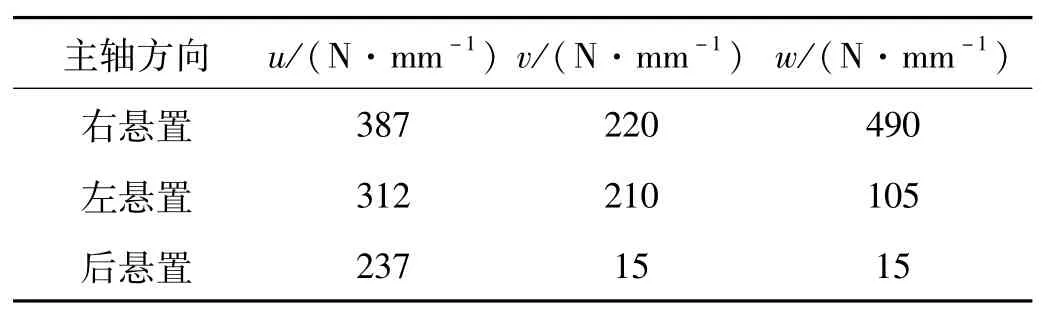
表4 悬置件主轴方向动刚度Tab.4 Powertrain mounts stiffness in main axle

用Matlab编程并计算现有悬置系统的固有频率和解耦率［4］，如表5所示：

表5 现有悬置系统固有频率和解耦率Matlab计算结果Tab.5 Matlab calculated frequency and decouple rate of old powertrain mounting system

从计算结果的固有频率来看，在z方向的固有频率为6．1 Hz，落在在4～8 Hz之间，而人体在垂直方向上对这个区间的频率最敏感［5］，需要避开。当发动机工作时，θx方向存在转动力矩激励［6］，此方向的固有频率要小于激励频率的才能达到隔振效果［7］，本车型发动机的怠速转速为700 r／min，也就是要小于16．5 Hz。原系统θx方向的固有频率为17．2 Hz，略大于要求值，原系统固有频率需要重新配置。

从计算结果的解耦率来看，z方向的解耦率为49．5%，θy方向的解耦率为61．2%。这两个方向为发动机的主要激振方向，期望这两个方向的解藕率达到90%以上［8］，原系统解耦率需要提高。

3 遗传模拟退火优化算法的实现

3.1 优化设计的目标函数

传统的优化方法是以悬置固有频率或者解耦率为优化目标，这无法解决本课题的问题，因为从上节悬置系统固有特性的分析中，发现悬置系统不仅固有频率配置不合理，而且解耦率也有待提高，所以本文选择固有频率的配置和六自由度解耦组成的统一目标函数作为优化目标函数，解决十二个关键性能参数的同时优化问题。

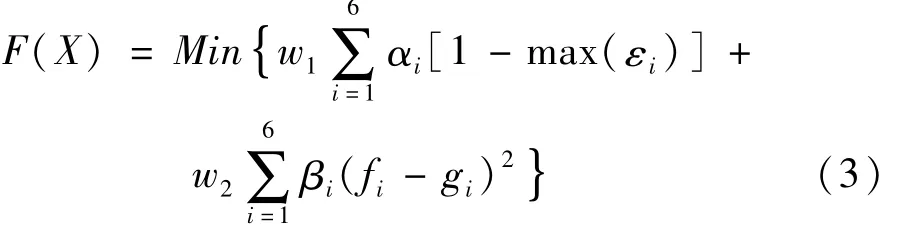
式中，εi为六个方向的解耦率；αi为六个方向解耦率的加权因子，取z方向的加权因子α3为0．3，θy方向的加权因子α5为0．3，其他四个方向的加权因子为0．1；fi为六个方向的固有频率；βi为六个方向固有频率的加权因子，取z方向的加权因子β3为0．3，θy方向的加权因子β5为0．3，其他四个方向的加权因子为0．1；gi是六个固有频率的约束范围；w1，w2是统一量纲系数。

3.2 优化设计变量

由于设计和制造成本的限制，本文以三个悬置元件在三个方向的主轴动刚度作为设计变量。包括右悬置三个主轴方向的刚度：ku1，kv1，kw1。左悬置三个主轴方向的刚度：ku2，kv2，kw2。

对于给定的一组优化设计变量，通过Matlab可以计算得到悬置系统六个方向的固有频率fi和解耦率εi，从而通过式3得到目标函数值。

3.3 约束条件

约束条件包括悬置系统固有频率的约束和悬置元件主轴刚度约束，本车型悬置系统固有频率的理论配置范围如表6所示。

一组优化设计变量可计算得到悬置系统六个方向的固有频率fi，对于gi的取值情况，可以分为三种情况，当悬置系统某一个方向的固有频率fi在约束的频率范围之内时，则令gi等于fi，当悬置系统某一个方向的固有频率fi小于约束频率范围的最小值时，则令gi等于gmin，当悬置系统某一个方向的固有频率fi大于约束频率范围的最大值时，则令gi等于gmax。

表6 悬置系统固有频率的配置Tab.6 Frequency allocation of powertrain mounting system

从隔振要求出发，悬置的刚度应设计得尽量小。为避免汽车起动、制动等瞬态工况下动力总成产生过大的位移量，从而和发动机外围件产生干涉，悬置的刚度不能太小，实际中，兼顾隔振性能和位移要求，并参考类似车型的设计数据，左右两个液压悬置元件主轴刚度的约束范围设定如下：

抗扭拉杆侧悬置主要受力方向为整车的前后方向，上下方向和左右方向几乎不受力，所以只要优化拉杆悬置ku3的刚度，kv3，kw3的刚度很小，作为优化设计变量的范围可以为0。

3.4 遗传模拟退火优化算法的设计

从式3悬置系统优化数学模型可以看出，很难用具体的数学表达式来表达优化变量和优化目标函数的关系，所以在求解过程中难以进行凹凸性分析以及梯度分析，传统的优化算法，如复合形法、二次规划法等，优化搜索是从解空间中的一个初始点开始最优解的迭代搜索，容易陷于局部最优解而使搜索过程停滞不前，所以解决这种问题一般采用智能算法。遗传算法是目前比较流行的一种智能算法，该算法全局搜索能力强［9］，但是进化后期搜索效率较低，在局部范围内寻找的次优解的概率大，而模拟退火算法局部寻优能力强的优点正好可以来弥补遗传算法的缺陷，这两种算法的结合称为遗传模拟退火算法，该算法用在悬置系统的优化设计中尚不多见。

遗传模拟退火算法首先初始化种群并计算各个体目标函数值和适应度值，根据适应度值，遗传算法进行选择、交叉、变异操作得到新种群，这时的新种群并不直接作为下一代的进化种群，而是需要计算新种群各个体的目标函数值，用模拟退火算法替代初始种群中的个体，更新后的初始种群作为下一代的进化种群。遗传模拟退火算法的参数设置如表7所示。

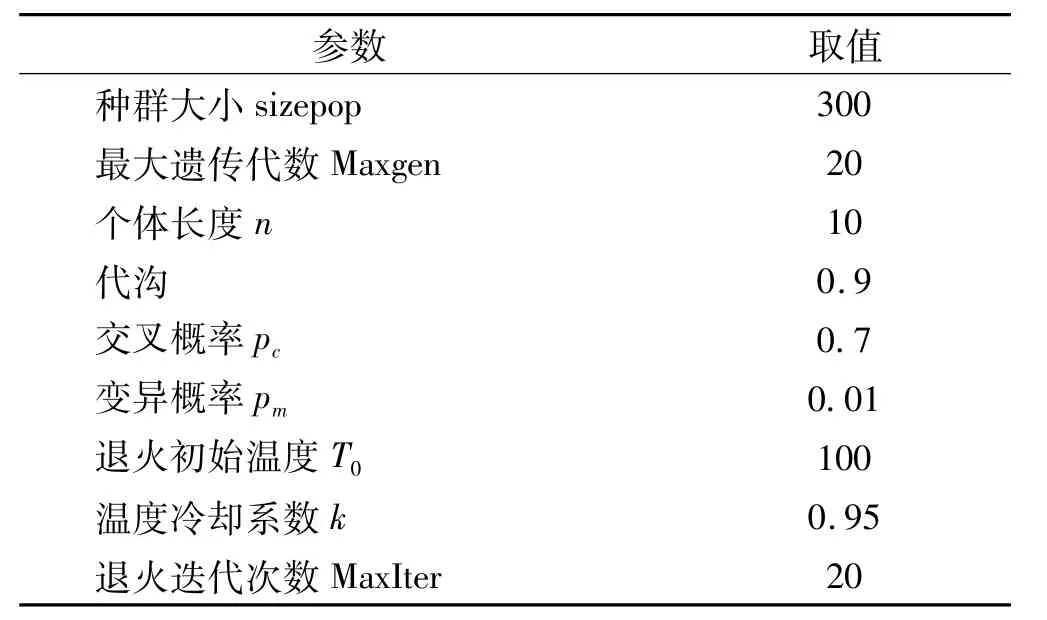
表7 遗传模拟退火算法参数设置Tab.7 Parameter of simulated annealing and genetic algorithm

优化流程图用图3表示，对优化流程解释如下：

（1）算法相关函数的选择：9个变量采用二进制的编码方式，每个变量使用n位编码，则染色体的长度为9×n；适应度函数采用排序的适应度分配函数：FintV＝ranking（Fi）；选择算子采用随机遍历抽样；交叉算子采用最简单的单点交叉算子；变异算子是以一定的概率产生变异基因数，用随机方法选出发生变异的基因。

（2）按照表7设定控制参数。

（3）生成初始种群Chrom，并计算每个个体的目标值Fi，i＝1，2，…，sizepop。

（4）设循环计数变量gen＝0。

（5）对种群Chrom实施选择、交叉和变异等遗传操作，对新产生的个体计算目标值F′i。若F′i＜Fi，则以新个体替代旧个体；否则，以概率P＝exp（Fi－F′i）接受新个体，舍弃旧个体。

（6）若gen＜Maxgen，则gen＝gen＋1，转至步骤（5）；否则，转至步骤（7）。

（7）若Iter＜MaxIter，执行降温操作Ti＝kTI，转至步骤（4），否则，算法结束，返回全局最优解。

3.5 优化步骤

（1）根据图3所示的优化流程图，编写Matlab优化程序。

（2）确定优化程序中的目标函数统一量纲系数w1和w2，首先将式（3）中w2取为0，只考虑解耦率对目标函数值的影响，将目标函数代入并运行Matlab优化程序，得到目标函数的最大值Fdmax和最小值Fdmin。同样的方法得到只考虑固有频率对目标函数值的影响时，目标函数的最大值Fgmax和最小值Fgmin。则w1和w2可由下式计算得到［7］：

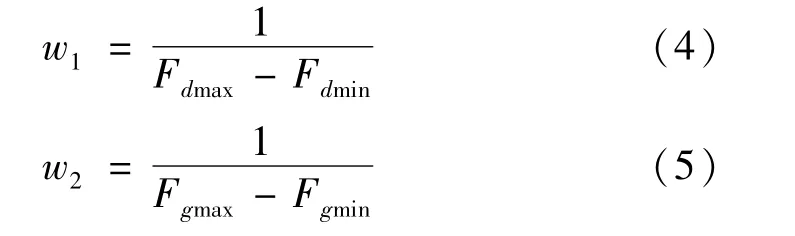
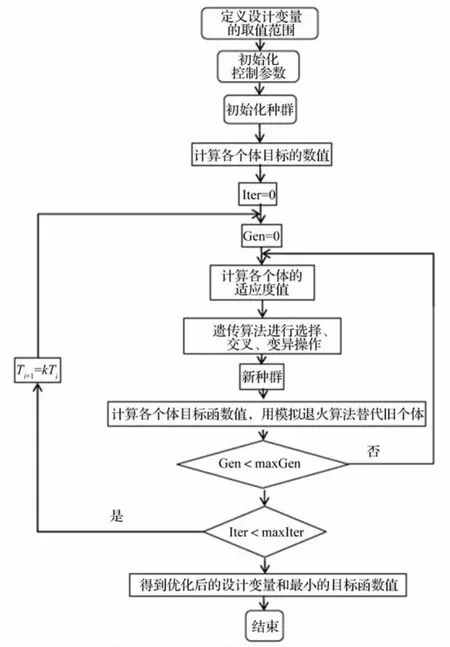
图3 遗传模拟退火算法的优化流程图Fig．3 Optimum flow chart of simulated annealing and genetic algorithm

（3）将带有w1和w2的目标函数代入优化程序，得到优化后的设计变量和最小的目标函数值。图4为某次得到的最优解目标函数值历程曲线。

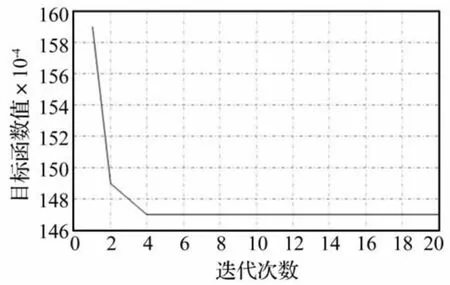
图4 某次得到的最优解目标函数值历程曲线Fig．4 The optimal solution of objective function value history curve

4 优化后固有频率和解耦率分析

表8优化后悬置元件的刚度值，表9为优化后的固有频率和解耦率。

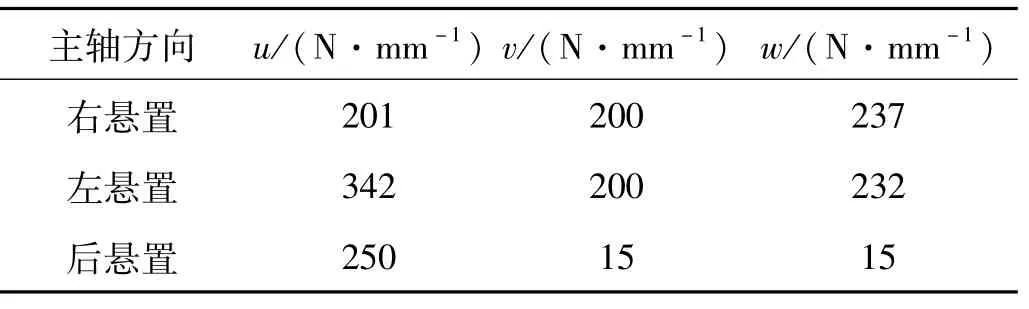
表8 优化后悬置件主轴方向动刚度Tab.8 Optimized powertrain mounts stiffness in main axle

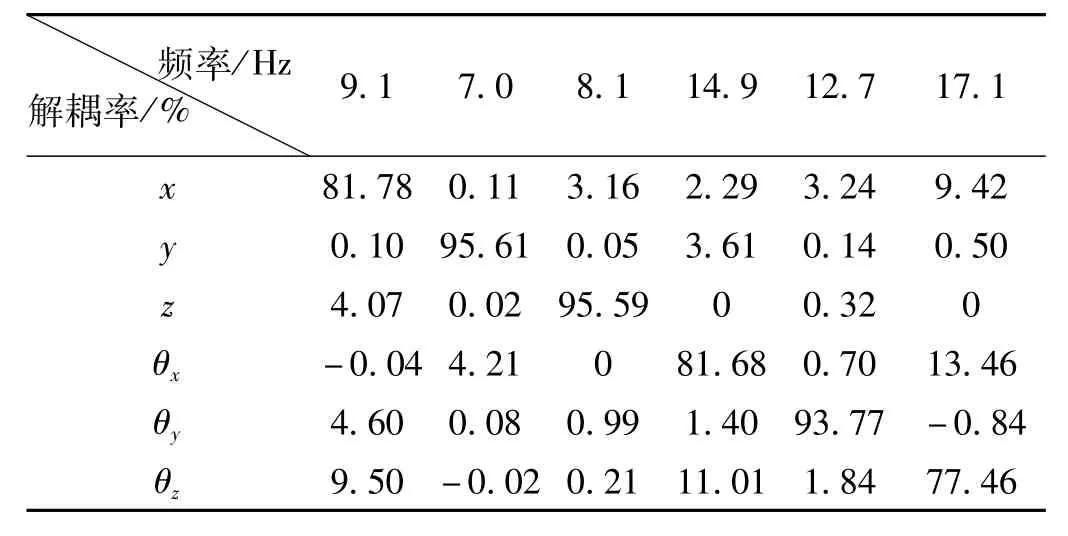
表9 优化后悬置系统固有频率和解耦率Matlab计算结果Tab.9 Matlab calculated frequency and decouple rate of new powertrain mounting system

从表5和表9对比可以看出，优化后z方向的固有频率由6．1 Hz上升到8．1 Hz，避开了人体垂直方向的敏感频率段。θx方向的固有频率由17．2 Hz降为14．9 Hz，小于16．5 Hz，达到了隔振理论的要求。

从优化前后的解耦率可以看出，z方向的解耦率由49．5%上升到95．6%。θy方向的解耦率由61．2%上升到93．8%，其他四个方向上的解耦率也有不同程度的提高。

5 优化后整车隔振效果评价

根据优化后的悬置元件刚度参数，试制新样件后组织换装，实车测量了新悬置系统的振动传递率，并和原左悬置的振动传递率作对比，如图5所示。

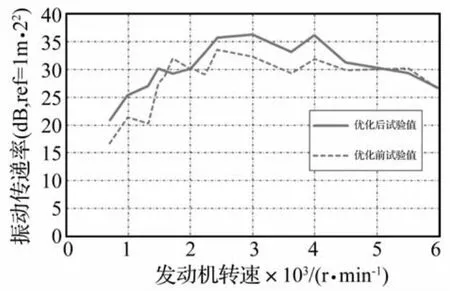
图5 左悬置z向振动传递率试验值比较Fig．5 Test transfer rate comparison of left mount in z direction

从图5中可以看出，优化后的悬置系统在左悬置低速段处的振动传递率均大于20 dB，在怠速时的振动传递率由16．7 dB上升到20．9 dB，发动机转速1 200 r／min时的振动传递率由20．7 dB上升到25．9 dB，达到了悬置系统的隔振设计要求。

6 结 论

本文以悬置系统的六个方向的固有频率和六个方向的解耦率为综合优化目标，应用遗传模拟退火算法优化了悬置系统的刚度参数。在整车上对优化后的悬置系统进行了实车试验，隔振传递率大于20 dB，达到了隔振要求。说明该算法可以用于悬置系统的优化设计，从而有效提高悬置系统的隔振效果。

［1］王峰．汽车动力总成悬置系统振动分析及优化设计［D］．上海：上海交通大学，2008．7．

［2］Zou Chun-ping，Hong Xing．Modal synthesis［J］．Journal of Sound and Vibration，2002，80（32）：105－112．

［3］Swanson D A，Wu H T，Ashrafiuon H．Optimization of aircraft engine suspension systems［J］．Journal of Aircraft，1993，30：979－984．

［4］Johnson S R，Subhedar J W．Computer optimization of engine mount systems［R］．SAE Paper．790974．

［5］时培成，陈无畏，高立新．基于蒙特卡罗法的动力总成悬置系统稳健性设计［J］．汽车工程，2010，32（8），707－710．

SHI Pei-chen，CHEN Wu-weil，GAO Li-xin，Robustness design of powertrain mount system based on monte carlo method［J］．Automotive Engineering，2010，32（8），707 －710．

［6］史文库，林逸，吕振华，等．动力总成悬置元件特性对整车振动的影响［J］．汽车工程，1997，19（2）：103－107．

SHI Wen-ku，LIN Yi，LÜ Zhen-hua，et al．Influence of characteristics of engine mount elements on vehicle vibration ［J］．Automotive Engineering，1997，19（2）：103－107．

［7］Tao J S，Liu G R，Lam K Y．Design optimization of marine engine-mount system［J］．Journal of Sound and Vibration，2000，235（3）：477－494．

［8］吴杰，周胜男．动力总成悬置系统频率和解耦率的稳健优化方法［J］．振动与冲击，2012，31（4）：1－7．

WU Jie，ZHOU Sheng-nan．Robustness optimization method for frequency and decoupling ratio of powertrain mounting systems［J］．Journal of Vibration and Shock，2012，31（4）：1 －7．

［9］周密，侯之超．基于遗传算法的动力总成悬置系统优化设计［J］．汽车技术，2006，9：13－16．

ZHOU Mi，HOU Zhi-chao，Optimization on engine mounting based on genetic algorithm［J］．Automobile Technology，2006，9：13－16．

Vibration isolation optimization of a vehicle powertrain mounting system based on simulated annealing and genetic algorithm

YAN Xiao-jun1，2，JIANG Wei-kang2，CAO Cheng1
（1．Shanghai Volkswagen Automotive Co．Ltd，Shanghai 201805，China；2．School of Mechanical and Power Engineering，Shanghai JiaoTong University，Shanghai 200240，China）

Aiming at vibration isolation effect of one vehicle powertrain mounting system was insufficient，its natural frequencies and the decouple rate of the system were taken as integrated optimal objectives，and the simulated annealing and genetic algorithm（SAGA）were used to optimize the mounting stiffness parameters．The optimized results showed that its natural frequency deployment is more reasonable and the decouple rate in the major vibration direction increases．The vehicle vibration isolation test results showed that the vibration isolation effects of the optimized mounting system meet design requirements．

powertrain；mounting system；vibration isolation；decouple rate；optimization；simulated annealing and genetic algorithm

TB53；U461

A

10．13465／j．cnki．jvs．2014．23．028

2013－10－21 修改稿收到日期：2013－12－04

严小俊男，硕士生，1981年6月生

蒋伟康男，博士，教授，博士生导师，1961年8月生