采煤机截割部传动系统的动力学仿真

赵丽娟，兰金宝

（辽宁工程技术大学机械工程学院，辽宁 阜新 123000）

采煤机截割部传动系统的动力学仿真

赵丽娟，兰金宝

（辽宁工程技术大学机械工程学院，辽宁 阜新 123000）

基于刚－柔耦合多体接触动力学理论，对采煤机截割部传动系统进行了研究，给出了其模型参数的确定方法。在RecurDyn软件环境中建立了截割部传动系统刚柔耦合多体接触动力学模型，并施加MATLAB计算出的基于实际工况的载荷。在仿真环境下直观动态地描述了齿轮啮合接触过程，计算出了各级齿轮的动态等效应力，并根据仿真结果对齿轮进行了优化。解决了大型机械传动机构进行柔性接触仿真的难题，增加了虚拟样机技术研究的可靠性，揭示了齿轮传动系统的刚度激励与啮合冲击激励引起响应的周期性波动现象。

齿轮传动；RecurDyn；多体动力学；接触力

齿轮传动是机械系统中广泛应用的一种传动形式，具有传动速度和功率范围大，传动效率高，结构紧凑等特点。近年来已有国内外学者采用虚拟样机技术对齿轮啮合接触过程进行了研究，取得了一些研究成果［1－3］，建立了轮系的非线性动力学方程并给出了数值解，但在求解的过程中要经过繁杂的迭代过程，对于具体工程问题，应用时还不够直观、方便。本文从接触理论的角度结合多体动力学仿真软件RecurDyn，基于某公司开发的免维护新型采煤机截割部仿真分析项目，对其传动系统进行动力学仿真，试图探讨描述齿轮动态啮合过程和齿轮传动动力学模型方法，为其动力学分析提供一种新的手段。

1 RecurDyn接触算法

接触计算是一个不断检测的过程，在每一个增量步，都需要通过检查几何位置来判断接触状态是否存在，并根据穿透深度及其变化来计算接触力。

1.1 齿轮接触模型

虚拟样机中的齿轮接触可以通过简化的圆弧来模拟其接触状况。如图1所示，弧k和弧l分别为齿轮i 和j的轮齿齿廓上的弧段，t点和p点分别为两个弧的中心点，在t点和p点上分别建立坐标系和，两个坐标系的X轴分别固定在弧段的起点方向上。坐标系XiYiZi和XjYjZj分别为齿轮i和j的坐标系，XYZ为全局坐标系。由图1可知，如果弧k中心点t到弧l中心点p的长度小于两弧半径和，则认为这两段弧接触。

弧k相对于全局坐标系的姿态由式（1）得到

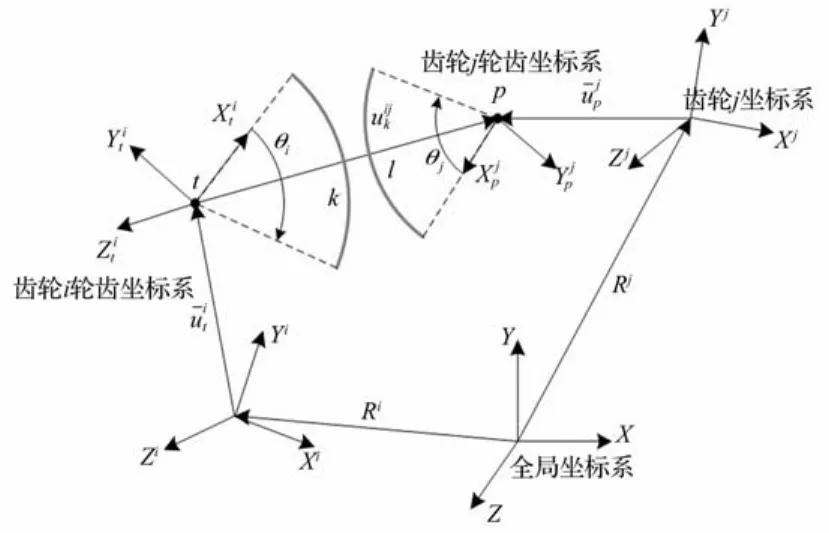
图1 弧—弧接触模型Fig．1 Arc-arc contact model

因此，弧l中心点p关于弧k中心点t的位置向量可由式（5）得到

式中：rt和rp分别为齿轮弧k和l的半径；wt和wp分别为轮齿的半齿宽。

在满足以上条件的基础上，还需要检查接触点是否在弧的范围内，即是否满足式（8）

式中：θm和θn分别为与齿轮弧k和l的坐标系的夹角；θk和θl分别为齿轮弧k和l的中心角。

如果满足式（1）至（8），那么穿透深度δij被定义为

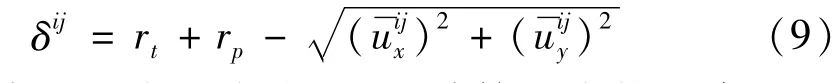
根据穿透深度的大小，即可计算出齿轮啮合时的接触力。

1.2 RecurDyn接触力计算模型

Lankarani提出了基于Hertz接触理论的非线性阻尼模型，其接触力可由式（10）得到

式中：k为接触刚度系数；c为阻尼系数；m1、m2、m3分别为刚度指数、阻尼指数及凹痕指数；δ和δ′分别表示穿透深度及接触点的相对速度（穿透深度的导数），这些参数取决于材料的类型、尺寸等。

图2 接触力计算模型Fig．2 The calculation model of contact force

根据模型尺寸及材料，得到接触力计算模型中刚度、阻尼、渗透量等参数的取值如表1。

表1 接触力计算模型参数Tab.1 The calculation of the contact force model parameters

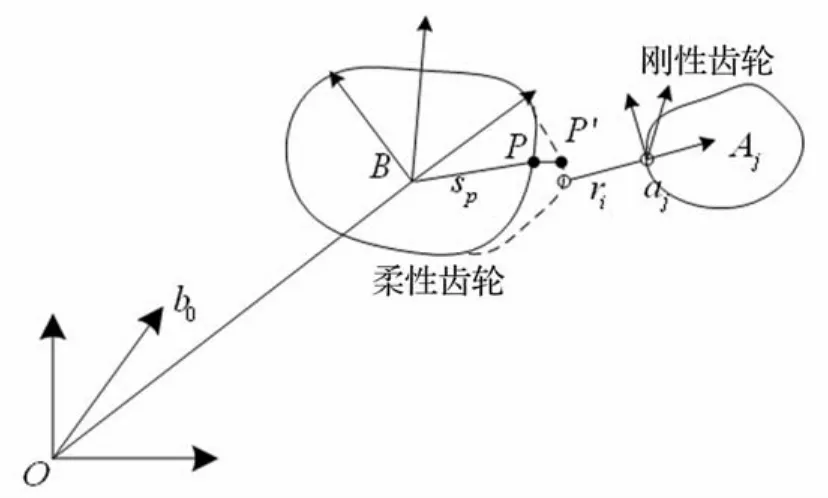
图3 采煤机多柔体系统示意图Fig．3 Multi-flexible body system schematic diagram of shearer

2 刚－柔耦合虚拟样机模型的建立

复杂煤层赋存条件下工作的采煤机是典型的刚柔耦合多体系统，滚筒截齿截割煤壁时，刚性构件的大位移运动与柔性构件的小变形运动相互影响，强烈耦合［4－5］。图3为多柔体系统示意图。其中B为柔性齿轮，Aj为刚性齿轮，O为惯性坐标系。aj为刚性齿轮Aj的局部坐标系，其原点设在刚性齿轮的内铰ri处。柔性齿轮上某一节点p的位置向量为

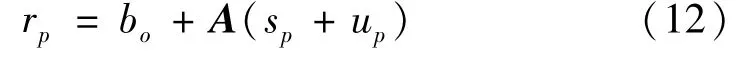
式中，rp是p点在惯性坐标系中的位置向量，bo为惯性坐标系原点到局部坐标系原点的位置矢量，A为局部坐标系相对惯性坐标系的变换矩阵，sp为柔性齿轮未变形时节点p在局部坐标系中的位置向量；up为相对变形量，可以用变形模态矩阵Φp与变形的广义坐标ξ的乘积来表示。对式（12）求导可得p点速度为

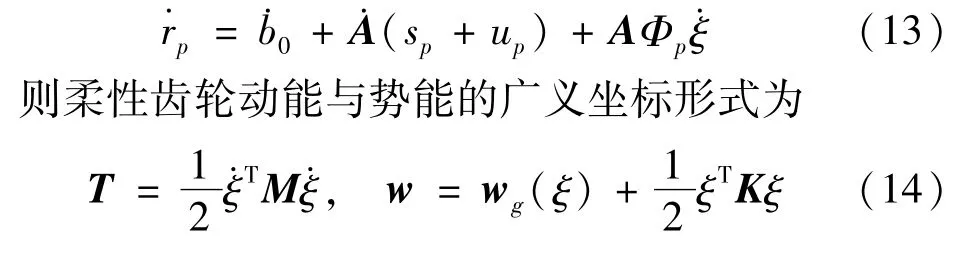
式中，M是广义质量矩阵，wg（ξ）为重力势能，K为广义刚度矩阵。将T、W以及能量损耗函数Γ代入式（15）的Lagrange方程

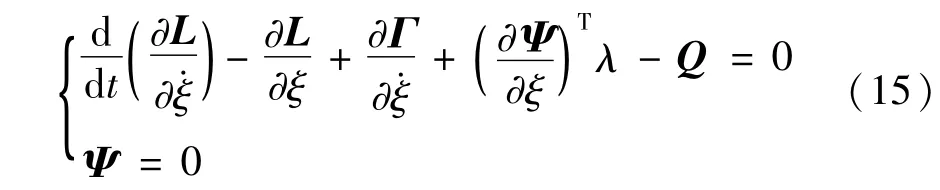
式中，则多柔体系统的运动微分方程为［6－9］

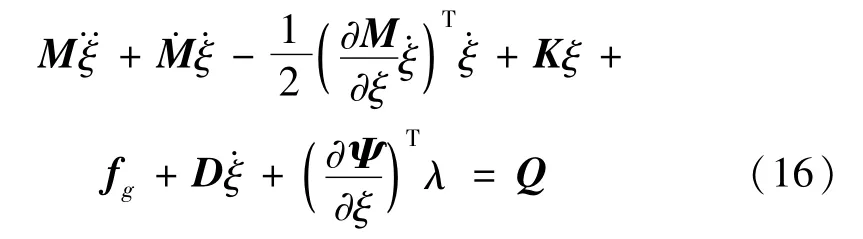
式中，L＝T－W；D为模态阻尼矩阵；fg为多体重力；λ为拉格朗日乘子；Ψ为约束方程；Q为外部施加的载荷；M·为柔性体质量矩阵对时间导数。

3 刚柔耦合动力学模型的建立和分析

3.1 截割部模型建立

多体动力学仿真软件RecurDyn的分析功能强大，而几何建模功能相对较差，选择专业三维实体造型软件Pro／E完成采煤机截割部主要零部件的建模与虚拟装配并进行静态干涉检查，略去对传动系统仿真影响较小的部分端盖、螺栓等小零件。

由于Pro／E与RecurDyn没有专用的接口，故将模型组件存为step（．stp）中性文件，并导入到RecurDyn软件中，将与传动系统无关的零、部件合并，以减少分析时间，重新定义材料，质量和marker点。添加约束后截割部如图4所示。

图4 RecurDyn中采煤机截割部导入图Fig．4 the import figure of shearer cutting part into RecurDyn

3.2 刚体柔性化

RecurDyn软件支持两种类型的柔性体，模态柔体（RFLEX）和有限元柔体（FFLEX），有限元柔体可以求解非线性的接触问题，这是RecurDyn的优势所在。但是柔性体数目的增加，会极大降低求解的速度，针对本文研究的问题，对离滚筒最近的输出端齿轮应用专业有限元软件ANSYS进行柔性化，生成RecurDyn所需要的有限元柔体文件，将此文件导入到RecurDyn中替换相应的刚性齿轮并完成约束、驱动与载荷的添加。

3.3 动力学仿真与可靠性分析

基于前苏联破煤理论，利用项目组开发的采煤机载荷模拟程序［10］，得到前滚筒抬起最大角度、截割煤岩坚固性系数f为3．11的全煤；牵引速度v＝8m／min工况的载荷力和载荷力矩，将Matlab所生成的载荷文本（．txt文件）导入RecurDyn中，施加在滚筒质心处，在RecurDyn后处理模块中提取模拟工况下的三向力与三向力矩如图5所示。

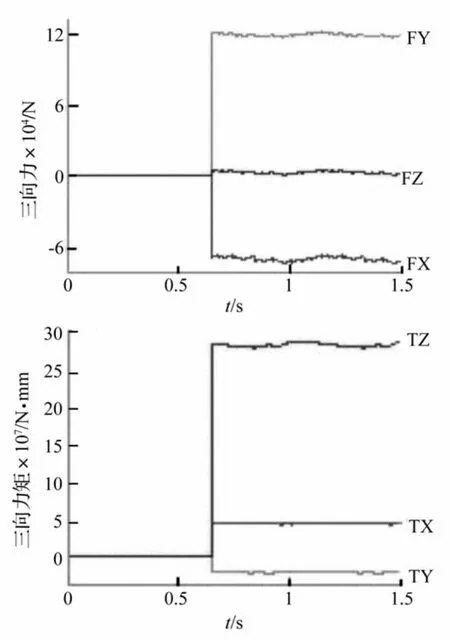
图5 滚筒三向力与三向力矩曲线Fig．5 Three-axis force and torque load curves for the drum

由图5可见，滚筒截割煤壁的瞬时，滚筒所受合力和合力矩最大，分别为139．63 kN和2．92×104N·m；稳定截割过程中合力和合力矩平稳波动，其平均值分别为138．66 kN和2．88×104N·m。

3.4 RecurDyn动力学仿真设置

按给定的工况施加驱动，主动轮上施加驱动转速1 500 r／min，在电机稳定后添加载荷，驱动使用渐进函数STEP施加，运动方程为

根据式（11）确定接触刚度系数k及阻尼系数c。按Hertz接触理论，可推导出接触刚度计算式为

式中：E为材料杨氏模量；b两齿轮有效啮合宽度；s为齿轮变位系数；r为刚度比。

考虑润滑条件下，根据经验，定义静、动摩擦因数分别为0．08和0．05，最大静、动摩擦对应的相对滑移速度分别为0．1 mm／s和1 mm／s。

选择HYBRID作为动力学模型的积分器，设定计算误差为0．01，最小积分时间步长为0．000 1 s，仿真输出步数为1 500步。

4 仿真结果及分析

对齿轮传动的动力学模型进行仿真，提取接触力和接触转矩如图6和图7所示。

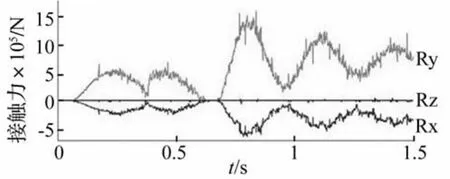
图6 刚－柔耦合接触力Fig．6 Rigid-flexible coupling contact force

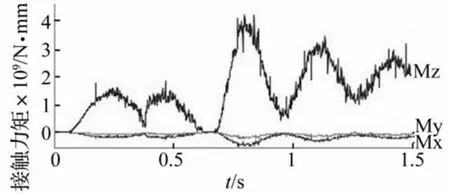
图7 刚－柔耦合接触转矩Fig．7 Rigid-flexible coupling contact torque

由图6和图7可见，在仿真开始阶段，接触力和接触转矩波动较大，运行平稳后波动幅度逐渐减小，而且呈明显的周期性，这是由于齿轮传动具有周期性的内部激励引起的［12］。在施加载荷后，接触力和接触力矩激增，并周期性衰减逐渐趋于稳定。由于考虑轮齿变形，刚柔耦合齿轮接触力较全刚体模型的接触力更加平缓，无尖峰状突变，与实际情况相符。接触应力最大值出现在0．795 s齿轮啮入过程齿顶处，此时等效应力为1 781．3 MPa，节点号为6 887，接触力最大时刻等效应力如图8所示，节点6 887等效应力时间历程曲线如图9所示。

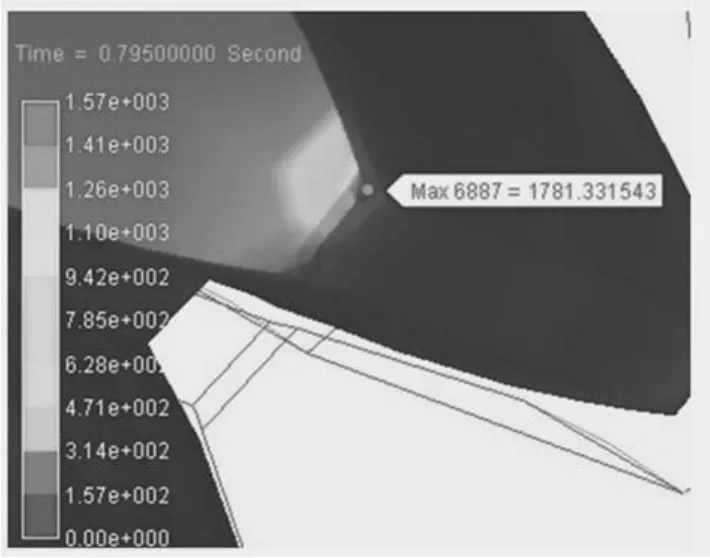
图8 接触力最大应力图Fig．8 Maximum stress of contact force

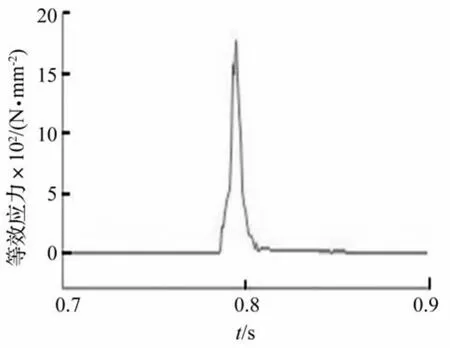
图9 最大应力点时间历程曲线Fig．9 Time history of curve maximum stress

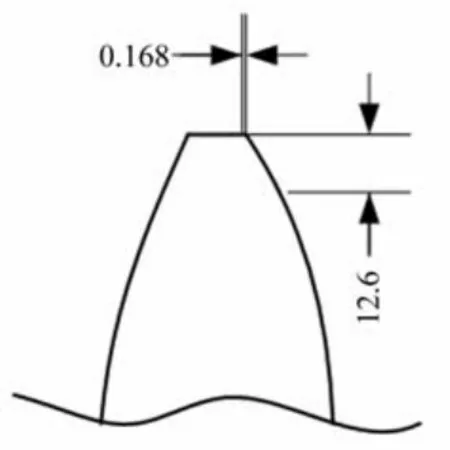
图10齿顶修缘尺寸Fig．10 Addendum modification size

通过接触力曲线可知，接触力等效应力最值均在800～1 400 MPa之间，而最大的等效应力为1 781．3 MPa，大于该齿轮材料的屈服强度1 570 MPa，可见该齿轮在传动过程中会出现局部屈服；齿轮上等效应力最大值在运动中重复出现，齿面发生塑性变形，破坏了齿面啮合的正确性，引起很大的动载荷，最终导致轮齿的失效。

由图8可见，最大应力出现在齿轮啮入过程齿顶处。齿轮啮合时，力的作用位置的任何突然改变都会引起高频振动，因此，需进行齿顶修缘，使力的转换时间尽可能延长，避免轮齿受到较大冲击。对于外啮合圆柱齿轮，当圆周速度大于6 m／s时，需要按7级精度进行齿顶修缘，选择e＝0．006。齿顶修缘尺寸如图10所示。

再次对齿轮传动的动力学模型进行仿真，得到接触应力最大值出现在0．738 s齿轮啮出过程分度圆靠近齿根处，此时最大等效应力为849．47 MPa，小于其材料的许用应力，满足要求。节点号为638，最值时刻等效应力如图11所示。

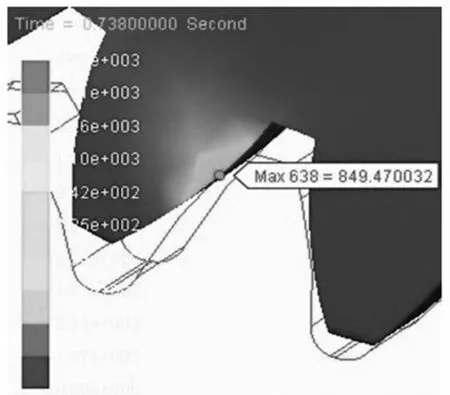
图11 接触力最大应力图Fig．11 Maximum stress of contact force

经过优化改进的采煤机截割部于2013年9月在神东大柳塔煤矿52 305工作面投入使用，如图12所示。一个月的试运转和完成配采任务后，安装了该摇臂的采煤机正式承担起了矿井主采任务，日采原煤3万吨以上，使用情况良好。

图12 在52305工作面投入使用的采煤机Fig．12 Coal mining machine put into use in 52305 working face

5 结 论

（1）建立了采煤机截割部传动系统的刚－柔耦合动力学分析模型，应用新一代多体动力学仿真软件RecurDyn成功计算了轮齿之间的动态接触力，同时得到了有限元柔体齿轮和刚性齿轮的动态等效应力分布云图，对齿轮进行齿顶修缘，避免了较大的等效应力对轮齿的破坏，优化后齿轮的最大等效应力为849．47 MPa，发生在柔性齿轮齿根处。

（2）利用RecurDyn多体动力学软件进行刚－柔耦合动态仿真，为刚－柔耦合齿轮多体动力学模型在工程分析中的应用奠定了基础。

（3）基于本文的研究方法，可以及早发现大型工矿装备在构件的大位移刚性运动与柔性构件的小变形运动相互影响，强烈耦合时的应力、变形规律，预测构件在交变载荷作用下的薄弱环节；基于仿真结果的优化可以极大地提高齿轮工作的可靠性，延长其使用寿命，提高企业的经济效益。

［1］毕凤荣，崔新涛，刘宁．渐开线齿轮动态啮合力计算机仿真［J］．天津大学学报，2005，11：991－995．

BI Feng-rong，CUIXin-tao，LIUNing．Involutegear dynamicmeshingsimulation［J］．JournalofTianjin University，2005，11：991－995．

［2］龙凯，程颖．齿轮啮合力仿真计算的参数选取研究［J］．计算机仿真，2002，06：87－88．

LONG Kai，CHENG Ying．Study on the selection of computer simulation for［J］．parameter Calculation of Gear Meshing Force Simulation，2002，06：87－88．

［3］阎绍泽，陈鹿民，季林红，等．含间隙铰的机械多体系统动力学模型［J］．振动工程学报，2003，03：36－40．

YAN Shao-ze，CHEN Lu-min，JI Lin-hong，et al．Dynamic modeling of multibody system［J］．Journal of Vibration Engineering with Clearance Joints，2003，03：36－40．

［4］刘杰，戴丽，赵丽娟，等．混凝土泵车臂架柔性多体动力学建模与仿真［J］．机械工程学报，2007，11：131－135．

LIU Jie，DAI Li，ZHAO Li-juan，et al．Concrete pump truck arm frame of flexible multi-body dynamics modeling and simulation of［J］．Mechanical Engineering，2007，11：131－135．

［5］陆佑方．柔性多体系统动力学［M］．北京：高等教育出版社，1996：l－15．

［6］廉自生，刘楷安．采煤机摇臂虚拟样机及其动力学分析［J］．煤炭学报，2005，6：801－804．

LIAN Zi-sheng，LIU Kai-an．Shearer rocker virtual prototype and its dynamic analysis［J］．Journal of China Coal Society，2005，6：801－804．

［7］韩清凯，罗忠．机械系统多体动力学分析、控制与仿真［M］．北京：科学出版社，2010：152－170．

［8］鲁明，胡聪良，孙伟，等．基于刚柔耦合的导轨滑块移动副建模［J］．中国工程机械学报，2010，3：279－281．

LU Ming，HU Cong-liang，SUN Wei，et al．Mobile guide based on rigid-flexible coupling pair of modeling［J］．China Mechanical Engineering Journal，2010，3：279－281．

［9］黄文虎，邵成勋．多柔体系统动力学［M］．北京：科学出版社，1996：32－51．

［10］赵丽娟，董萌萌．含硫化铁结核薄煤层采煤机工作机构载荷问题［J］．煤炭学报，2009，34（6）：840－844．

ZHAO Li-juan，DONG Meng-meng．With iron ore working mechanism of thin coal seam shearer load problem［J］．Journal of China Coal Society，2009，34（6）：840－844．

［11］Ebrahimi S，Eberhard P．Rigid-elastic modeling of meshing gear wheels in multibody systems［J］．Multibody Syst Dyn，2006，16：55－71．

［12］李润方，王建军．齿轮系统动力学［M］．北京：科学出版社，1997．

Dynamic simulation for transmission system of coal winning machine cutting part

ZHAO Li-juan，LAN Jin-bao
（School of Mechanical Engineering，Liaoning Technical University，Fuxin 123000，China）

To study transmission system of a coal winning machine's cutting part，the theory of rigid-flex coupled multi-body system dynamics was applied，a method for determining its model parameters was presented．The rigid-flexible coupled multi-body contact dynamic model for the transmission system was built in RecurDyn software environment and MATLAB was employed to calculate the loads under the actual conditions．In order to optimize the simulation results of the gear system，the gear meshing process was described intuitively and dynamically and the dynamic equivalent stresses of gear pairs were calculated under the simulation environment．The problems of a large mechanical transmission mechanism's flexible contact simulation were solved and the reliability of virtual prototype technology was improved．The periodic oscillation phenomen a of the responses of the gear transmission system to the stiffness excitation and meshing impact excitation were revealed．

gear transmission；RecurDyn；multi-body dynamics；contact force

TH132．413

A

10．13465／j．cnki．jvs．2014．23．019

2013－10－09 修改稿收到日期：2013－12－24

赵丽娟女，博士，教授，博士生导师，1964年4月生