基于CAE/CAT/CAO的齿轮箱轴承结合部等效刚度识别方法
楼江雷,唐进元
(中南大学高性能复杂制造国家重点实验室,中南大学机电工程学院,长沙 410083)
基于CAE/CAT/CAO的齿轮箱轴承结合部等效刚度识别方法
楼江雷,唐进元
(中南大学高性能复杂制造国家重点实验室,中南大学机电工程学院,长沙 410083)
基于CAE/CAT/CAO技术,提出一种有限元模态分析、试验模态分析与Isight集成优化方法相结合的精确识别轴承结合部等效刚度的方法:①采用Abaqus有限元分析软件建立齿轮箱有限元分析模型,通过spring单元模拟轴承三个方向的等效刚度,并将其作为设计变量;②基于LMS模态测试分析系统对齿轮箱进行试验模态分析,得到包含轴承结合部信息的各阶固有频率和振型,并以试验模态分析得到的固有频率值作为优化目标值;③通过Isight软件集成Abaqus对轴承刚度进行寻优,使有限元模态分析的结果与试验模态分析的结果相一致。分析结果表明,该方法综合考虑了齿轮轴、箱体的柔性,具有较高的精度,优化后的齿轮箱有限元模型与试验模型动态性能一致性好。
齿轮箱;轴承刚度;有限元模态分析;试验模态分析;CAE/CAT/CAO
在建立具有结合部的多零件系统动力学分析模型时,普遍存在结合部难于精确模拟问题,联接部位的刚度、阻尼特性等结合部参数对机械结构的动态特性却有着举足轻重的影响[1]。齿轮箱的振动是轴、齿轮、轴承、箱体等多种振动的综合作用,齿轮轴系和箱体通过轴承组成一个系统。因此,轴承的支承刚度对齿轮系统的动力学特性有重要的影响,它将直接影响到轴系和箱体的固有频率和频响。准确地建立齿轮箱的动力学有限元模型,关键技术之一在于准确地识别轴承结合部的参数。
理论计算与试验测试相结合的方法,是当前结合面等效参数识别中比较经济有效的途径。Fritzen等[2-3]曾用整体结构的动态实验数据,对结构做整体有限元反解,从而获得结构的刚度与阻尼矩阵,但是这样做不仅计算量很大,而且很难得到其反解;Choy等[4]采用三自由度的等效弹簧模型来模拟轴承三个方向的刚度值,通过有限元分析与动态试验结果的相关性分析验证了这种方法的可行性;杨家华等[5]在模态分析的基础上应用结合面单元建立了机床结构的动力学方程,经过优化计算识别了机床立柱和床身之间的结合面参数;李润方等[6-7]采用有限元法和试验模态分析相结合,建立了齿轮齿轮传动模型的模态坐标模型和物理坐标模型,然后通过齿轮轴的各个方向的锤击试验得到了轴承的刚度和阻尼,但在轴承参数识别过程中假定了齿轮箱体是刚性的,忽略了锤击试验时齿轮箱体的柔性对齿轮轴系耦合振动的影响。
模态分析是研究结构动力特征的一种主要方法,分为理论模态分析和试验模态分析[8]。对于简单的单个部件,边界条件理想,有限元模态分析计算精确度很高;但对于多零件组成的复杂机械装置,由于存在结合部联接、边界条件难模拟的问题,有限元模态分析结果精度较差。而试验建模方法是对现有结构的典型工况进行动态试验,所以避免了结构各结合部联结条件及其等效动力学参数,阻尼假设,各种边界条件的近似及简化,以及近似计算等带来的误差,故所得试验模型与现有机械结构的实际工况有较高精度的吻合。因此,可采用试验结果对有限元模型进行参数修正来获得结合部的参数,并建立更准确的有限元模型。
本文基于CAE/CAT/CAO技术,提出一种有限元模态分析和试验模态分析相结合精确识别轴承结合部等效刚度的方法。方法的主要内容是:综合考虑了齿轮轴及箱体的柔性,建立齿轮箱有限元分析模型,通过Spring弹性单元模拟轴承三个方向的等效刚度,并将其作为设计变量,以试验模态分析得到的固有频率值作为目标值,通过优化方法对轴承的等效刚度进行参数寻优,使得有限元模态分析与试验模态分析得到的固有频率相一致,此时Spring参数变量的值即为轴承的等效刚度值。该方法通过有限元模态分析与试验模态分析相结合,准确地识别了轴承三个方向的等效刚度值,建立的齿轮箱有限元分析模型有较高的精度和工程应用价值。
1 齿轮箱有限元模态分析关键技术
有限元模态分析是根据结构的几何形状、边界条件和材料属性,不考虑阻尼,把结构的质量分布和刚度分布用质量矩阵和刚度矩阵表示出来,然后通过特征值提取算法得到结构的模态参数。
论文研究使用的齿轮箱为开式,如图1所示,齿轮箱中的两个直齿轮型号相同,模数为4,齿数为61,传动比为1,轴承型号为6210-LS,齿轮箱底座通过地脚紧固螺栓和压块固定在实验室的试验台上。

图1 试验齿轮箱Fig.1 Test gearbox
齿轮箱体的结构比较复杂,箱体上分布有倒角、凸台、螺栓联接孔、密封圈等。实际上,箱体结构上分布的这些微小特征对模型的质量、质心等影响不大,而对网格划分带来比较大的麻烦,因此在建立有限元模型时,对箱体实际结构进行了适当的等效简化处理。
1.1 网格单元的选择
采用不同的网格单元可能对最后的分析结果影响很大。对于三维问题,Abaqus中主要提供Hex单元(六面体单元)和Tet单元(四面体单元),按照节点位移差值的阶数,可分为线性单元、二次单元和修正的二次单元。因此首先使用各种不同的单元类型来对简单的单个齿轮部件进行有限元模态分析,其中各种单元网格具有相同的种子分布,分析结果见表1所示。
对各种三维实体单元的单个齿轮模态分析结果进行比较,可以看出,除四面体线性单元(C3D4)、六面体线性完全积分单元(C3D8)和六面体线性缩减积分单元(C3D8R)外,采用其他各种单元类型得到的结果差别不大,都具有较高的精度;基于相同的网格种子,使用四面体二次单元与六面体二次单元得到的结果很接近,但四面体二次网格的计算代价更大一些。四面体单元网格,可以在装配体(Assembly)上直接划分,而不必对每个部件都进行剖分,在建模效率上高一些,对于模态分析而言,其精度已足够,求解效率也可接受。考虑到方便划分网格,且各个部件网格类型要统一,因此,采用四面体二次单元(C3D10)来统一划分网格。
1.2 定义结合部及边界条件
对于轴承结合部,在Abaqus中可以采用Spring弹簧单元来模拟轴承三个方向的等效刚度。首先将齿轮轴与轴承内圈、箱体与轴承外圈的接触进行绑定处理;在轴承内圈与外圈的圆心位置分别设置参考点,并与各自对应的参考点进行耦合处理;在参考点之间添加Spring弹簧单元,设置X,Y,Z方向的刚度值,分别模拟轴承三个方向的刚度特性。由于四个轴承同型号,安装方式、负载均相同,因此四个轴承的等效刚度值可认为是相同的,有限元模型中引入了3个参数变Kx,Ky,Kz,初始值均设置为1×108N/m。

表1 各种三维实体单元的模态分析结果比较Tab.1 The comparison of results of modal analysis through different 3D solid element
考虑到实际安装的齿轮副在啮合线的方向上存在0.733 7 mm(实际测量得到)的侧隙,在进行模态试验的时候齿轮副其实是没有啮合相互作用的,其对轴承等效刚度的识别不存在影响,因此忽略齿轮副的啮合约束。齿部属于不规则体,繁密的网格会增加计算负担,因此在保证质心及质量的前提下,将齿轮简化为圆柱体。
齿轮箱装配时,还存在齿轮和轴的键连接,齿轮箱顶盖和齿轮箱底座的螺栓连接等。相较于轴承结合部,它们对齿轮箱的动态特性影响很小,可以将它们看成刚性连接。齿轮箱底座通过地脚紧固螺栓和压块固定在试验台上,因此对齿轮箱底座的下表面施加固支边界条件。
齿轮箱有限元模型如图2所示,整个模型由19 062个单元,35 724个节点组成。
定义分析步类型为频率提取分析步,采用Lanczos方法提取特征值,提交分析作业,在后处理中提取有限元模态分析结果。齿轮箱系统的各阶模态中,对轴承刚度较敏感的是轴系的固有频率,而试验齿轮箱传动比为1,输入轴输出轴是对称的,在分析结果中也表现出对称相近的固有频率,因此只提取输出值的前5阶固有频率和振型列入表2。

图2 齿轮箱有限元模型Fig.2 The finite element model of gearbox
2 齿轮箱试验模态分析关键技术
试验模态分析是理论模态分析的逆过程,通过实验测得结构上的激励和响应的时间历程,运用数字信号处理技术求得频响函数或脉冲响应函数,然后运用参数识别方法求得系统模态参数。
实验采用比利时LMS公司的模态测试分析系统,该系统由激振系统、测量系统和分析系统组成。激励方式可以有锤击激励、激振器激励,响应信号由加速度传感器获取,通过LMS测试前端及LMS Test.lab对模态试验的输入和输出信号进行采集、处理和分析。
2.1 单个部件有限元模态分析与试验模态分析比较
为了验证试验模态分析与有限元模态分析的精度,对单个齿轮进行模态试验,然后与齿轮的有限元模态分析结果进行比较。将齿轮用弹性绳悬挂起来,布置16个测点,在测点9和10的位置分别固定一个单向加速度传感器,采用移动力锤法对齿轮各个测点施加脉冲激励。传感器安装及测点布置如图3所示。

图3 传感器安装及测点布置Fig.3 The installation of sensors and test points arrangement
单个齿轮有限元模态分析与试验模态分析得到的前六阶固有频率比较如图4所示。从图中看出,单个齿轮的有限元模态分析与试验模态分析结果很接近,分析误差原因,主要是有限元模型结构等效简化及离散化带来的误差和试验过程中测量及信号处理过程中的误差。
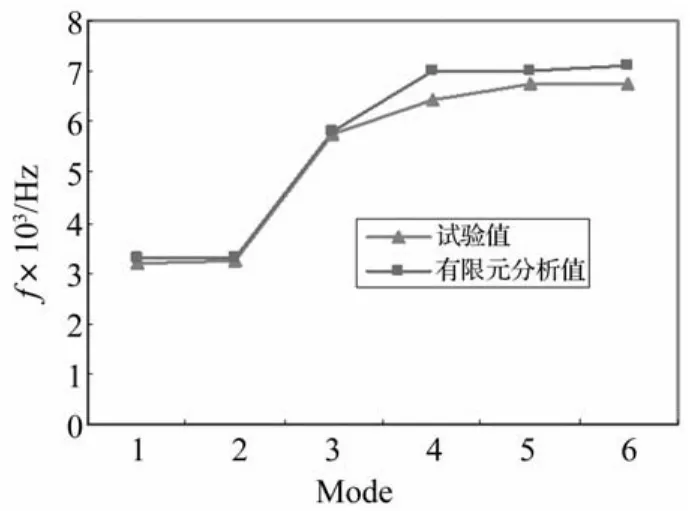
图4 单个齿轮部件有限元模态分析与试验模态分析结果比较Fig.4 The comparison of results of finite element modal analysisand experimental modal analysis
2.2 齿轮箱激振器试验
为了获得更大的激励能量和更好的激励效果,齿轮箱的模态试验采用激振器激励,试验方式为SIMO(单点激励多点输出)。激振头与测点表面用胶水固定,三向加速度传感器与测点表面用蜂蜡固定,激振头与测点表面用胶水固定,总共布置52个测点,通过移动4个三向加速度传感器分批获得齿轮箱上的响应信号。激振器及测点布置如图5所示。

图5 激振器及测点布置Fig.5 The arrangement of exciter and test points
激振器的激励信号采用猝发随机激励,模态参数识别方法采用Polymax算法。模态试验得到输出轴前5阶固有频率和振型,与有限元模态分析得到的结果进行比较,如表2及图6所示。

表2 齿轮箱模态分析结果比较Tab.2 Comparison of Modal analysis results of gearbox

图6 模态振型比较Fig.6 Comparison of modal shape
从齿轮箱有限元模态分析与试验模态分析的比较结果看,振型都能对应上,但是固有频率值有较大的偏差,需在保证振型对应的前提下,优化有限元模型中Springs单元的参数值,使得有限元模态分析的固有频率值尽量与实验模态分析得到的固有频率值接近。
3 基于Isight的轴承结合部参数寻优
Isight是一款用于多学科多目标优化设计的CAO (Computer Aided Optimization)软件,通过将不同的CAE软件集成到Isight中,采用相应的优化算法进行优化分析。在齿轮箱有限元模态分析和试验模态分析的基础上,采用Isight优化分析软件对轴承的刚度参数进行寻优,使得有限元模态分析的结果与试验模态分析的结果相一致。
3.1 结合部参数寻优数学模型
本次优化为多目标优化,一般情况下,多目标优化问题的各个子目标之间是矛盾的,一个子目标的改善有可能会引起另一个或者另几个子目标的性能降低,也就是要同时使多个子目标一起达到最优值是不可能的,而只能在它们中间进行协调和折中处理使各个子目标都尽可能地达到最优化[9]。
多目标优化问题的数学模型可表示为

式中x为D维设计变量,y为目标向量,N为优化目标总数,F(x)为目标函数,fn(x)为第n个目标函数,gi(x)为第i个不等式约束、hj(x)为第j个等式约束,xd-min和xd-max为每维设计变量搜索的上下限。
论文取设计变量为有限元模型中Spring单元参数Kx,Ky,Kz,即
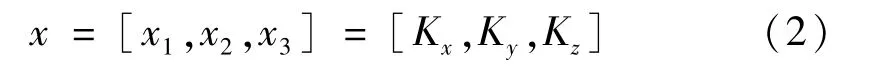
式中Kx为轴承轴向方向等效刚度,Ky为轴承径向水平方向等效刚度,Kz为轴承径向竖直方向等效刚度。
论文取优化目标为有限元模态分析得到的固有频率与试验模态分析得到的固有频率之差,即

论文取不等式约束为有限元模态分析与试验模态分析的每一阶固有频率之差的绝对值小于等于一个给定的值,本文经过试算,取给定的不等式约束范围值为50 Hz,设计变量的取值在5×106~5×108N/m之间,即:

3.2 优化历程及结合部参数寻优结果
Isight提供了与Abaqus的直接接口,可以在Isight中直接调用Abaqus计算数据,为了减少实际仿真软件的调用次数,提高优化分析任务的效率,首先对设计变量进行试验设计,得到近似模型。采用最优拉丁超立方[10](Optimal Latin hypercude)设计方法对设计变量在可行域之内均匀采样,设置样本点数为100,通过试验设计得到的样本数据,基于响应面模型得到设计变量与目标变量之间的近似模型,运用近似模型替代仿真程序,定义设计变量、设计目标及设计约束,采用NCGA[11]多目标遗传算法进行模型优化。
通过88次的迭代运算过程后,算法收敛,得到一组不同权值的Pareto解集,利用Isight自带的Pareto解集后处理模块得到设计变量取不同权值时优化目标的响应及Pareto解的分布,当取权值Kx∶Ky∶Kz=1∶1∶1时得到最优解,此时得到轴承等效刚度参数寻优的结果,如表3所示。

表3 参数寻优结果Tab.3 Results of parameter optimization
将优化前后有限元模态分析得到的固有频率与试验值进行比较,如图7所示。

图7 优化前后分析值与试验值比较Fig.7 Analysis values before and after optimization Compared with the test results
优化前,有限元模态分析得到的固有频率值与试验值最大误差达39.4%,优化后最大误差减小到4.9%,有限元模型的精度得到了很大的改善。
4 结 论
(1)论文工作表明,在有限元模态分析与试验模态分析的基础上,采用ISIGHT软件的集成优化方法对轴承结合面等效刚度进行识别,能得到较理想的结合面等效刚度,为有限元精确建模提供了基础参数。
(2)为了保证该方法的可靠性,须保证有限元模态分析和试验模态分析的精度,在优化时,应合理选定模态的数目,太少会得不到最优解导致识别误差,太多会增加数据处理的工作量,一般可取反映结合部特性的振动模态。
(3)本文给出CAE/CAT/CAO相结合方法得到精确的齿轮箱有限元分析模型,给出的详细技术细节与方法对其他机械装置的整体建模具有参考价值。
[1]张学良,徐格宁,温淑花.机械结合面静动态特性研究回顾及展望[J].太原重型机械学院学报,2002,23(3):276 -281.
ZHANG Xue-liang,XU Ge-ning,WEN Shu-hua.Review and prospect of the research on the static and dynamic characteristics of machine joint surfaces[J].Journal of Taiyuan Heavy Machinery Institute,2002,23(3):276 -281.
[2]Fritzen C P.Identification of mass,damping,and stiffness matrices of mechanical systems[J].Journal of Vibration Acoustics Stress and Reliability in Design,1986,108(1):9 -16.
[3]NalitolelaN,PennyJ,FriswellM.Updatingmodel parameters by adding an imagined stiffness to the structure [J].Mechanical Systems and Signal Processing,1993,7(2):161-172.
[4]Choy F K,Ruan Y F,Zakpajsek J,et al.Modal simulation of gear box vibration with experimental correlation[J].Journal of Propulsion and Power,1993,9(2):301-306.
[5]杨家华,陈为福,黄旭东,等.机床床身立柱结合面参数识别的研究[J].北京工业大学学报,1999,25(1):44-49.
YANG Jia-hua,CHEN Wei-fu,HUANG Xu-dong,et al.Reserch of joint surface parameter idengtification for bed column of machine tool[J].Journal of Beijing Polytechnic University,1999,25(1):44-49.
[6]李润方,韩西,林腾蛟,等.齿轮传动系统结合部动力学参数识别[J].中国机械工程,2001,12(12):1333-1335.
LI Run-fang,HANG Xi,LIN Teng-jiao,et al.Joint structure dynamic parameter identification for gear transmission system [J].China Mechanical Enginering,2001,12(12):1333 -1335.
[7]韩西,李润方,林腾蛟,等.齿轮轴横向弯曲振动结合部参数识别[J].机械设计与研究,2000,2(2):31-33.
HANG Xi,LI Run-fang,LIN Teng-jiao,et al.Joint structure parameter identification for lateral bending vibration of gear shaft[J].Machine Desigh and Research,2000,2(2):31 -33.
[8]傅志方.振动模态分析与参数辨识[M].北京:机械工业出版社,1990.
[9]肖晓伟,肖迪,林锦国,等.多目标优化问题的研究概述[J].计算机应用研究,2011,28(3):805-808.
XIAO Xiao-wei,XIAO di,LIN Jin-guo,et al.Overview on multi-objectiveoptimizationproblemresearch[J].Application Research of Computers,2011,28(3):805 -808.
[10]Park J S.Optimal latin-hypercube designs for computer experiments[J].JournalofStatisticalPlanningand Inference,1994,39(1):95-111.
[11]Watanabe S,Hiroyasu T,Miki M.NCGA:Neighborhood cultivation genetic algorithm for multi-objective optimization problems[J].GECCO Late Breaking Papers,2002:458 -465.
A method of equivalent stiffness identification for bearing joint of a gearbox based on CAE/CAT/CAO
LOU Jiang-lei,TANG Jin-yuan
(State Key Laboratory of High-performance Complex Manufacturing,School of Mechanical and Electrical Engineering,Central South University,Changsha 410083,China)
Based on CAE/CAT/CAO technology,a method to identify bearing stiffness of a gearbox was proposed with the combination of finite element modal analysis,experimental modal analysis and Integrated optimization of isight.Firstly,the finite element analysis model of a gearbox was built with the finite element analysis software Abaqus,and a spring element was used to simulate the equivalent stiffnesses of the bearing in 3 directions,they were taken as design variables.Secondly,the natural frequencies and vibration modal shapes containing information of bearing joint interfaces were acquired with the experimental modal analysis of the gearbox using LMS modal test and analysis system,and the natural frequencies acquired from tests were taken as the optimal objective values.Finally,the results of finite element modal analysis and those of experimental modal analysis were made to be in consistent through optimization of bearing stiffnesses using Abaqus combined with integrated Isight.Analysis results showed that the proposed method considers the flexibility of gear shaft and gear box,it has a higher precision,and there is a good agreement between the dynamic performances of the finite element model of the gearbox after optimization and those of the test model.
gearbox;bearing stiffness;finite element modal analysis;experimental modal analysis;CAE/CAT/CAO
TH132.41;TH113.1
A
10.13465/j.cnki.jvs.2014.23.015
973计划项目(2011CB706800);国家自然科学基金项目(51275530)资助
2013-08-20 修改稿收到日期:2013-10-23
楼江雷男,硕士生,1989年生
唐进元男,硕士,教授,1962年生

