爆炸容器法兰变形试验研究与数值模拟
王等旺,李 捷,王 昭,随亚光,唐仕英,李 焰
(西北核技术研究所,陕西西安 710024)
0 引言
法兰接头是爆炸容器密封的关键构件,是由法兰、垫片和螺栓连接件构成的独立组件,其作用是使容器的各承载壳体组合在一起,抵抗内部载荷的作用、并保证连接部位的密封性[1]。容器内炸药爆炸时内部将产生高温、高压的气体产物,一旦发生泄漏,将产生严重的次生灾害,严重威胁容器本体、周围设备及人员的安全,因此容器法兰的设计将对爆炸容器的安全评估和保障试验的安全性有着关键作用[2-5]。在化爆试验中,经常出现爆后容器筒体连接法兰密封面严重泄漏现象,图1示出爆后容器法兰变形情况。法兰部位发生塑性变形,使法兰的外圆柱面变成圆锥面,造成接触平面内凹,使得O形橡胶密封圈密封失效,致使内部爆炸气体外泄。目前,爆炸容器的法兰设计还没有专门的设计标准,大多是参考压力容器法兰设计方法进行设计,再通过原型或缩比考核试验的方式来验证。用这种方法设计的爆炸容器法兰虽然是安全的,但以此设计的爆炸容器法兰存在尺寸大、成本高、运输难等问题,其主要原因是没有考虑法兰在筒体塑性条件下的法兰结构响应,没有充分利用法兰结构在保持足够密封能力前提下的承载能力。有关爆炸容器法兰结构优化设计的研究工作较少,有待进一步开展理论分析和试验研究。

图1 化爆试验容器法兰变形情况
1 爆炸容器法兰载荷分析
密封容器中高能炸药爆炸,除对容器器壁施加瞬态冲击载荷外,随之在容器内部还将产生一个应力幅值比冲击载荷峰值小得多的静态气体压力(见图2)。由于爆轰产物与周围介质的热传导,爆炸产物气体的温度在不断下降,因而气体压力也随之下降,这种压力的改变相对是缓慢的,因此称之为准静态压力。冲击波压力和准静态压力是内部炸药爆炸载荷对爆炸容器的连续作用,在时序上有先后之分。冲击波压力峰值高、作用时间短;准静态压力峰值低、作用时间长,容器的结构响应也主要在准静态压力的作用时间内。

图2 密封容器筒体上的典型压力波形
一般在爆炸容器设计中忽略上述准静态气体压力,但定量分析准静态压力随时间的变化规律及最终压力状态具有重要的科学和工程意义。TROTT 等[6]曾发现导致直径 0.61 m,壁厚12.7 mm球形爆炸容器破裂的主要原因就是气体产物的准静态压力作用的结果,而非瞬态的爆炸冲击载荷。1999年,美国进行的OBOE系列次临界试验,准静态压力也是进行容器设计时所需考虑的主要参数[7]。美国学者 SHELL等[8]的数值计算表明,对于质量较小的核装置和容器内接近真空的初始条件下,后期准静态压力会使容器壁出现较严重的屈曲变形,局部应变会显著增大,可能比由冲击载荷引起的应变峰值高约2~4个数量级。在爆炸容器设计中,容器壁厚最小值、法兰结构和密封设计主要取决于爆后准静态压力。另一方面,对于大当量爆炸容器设计,通常采用双层或多层筒体结构:早期的冲击波载荷主要被内层筒体消耗,外层筒体将主要承受准静态压力的作用。容器法兰是连接容器最外层的重要部件,容器整体密封的有效性很大程度上取决于法兰在准静态载荷下的密封性能,这也使得研究准静态压力下爆炸容器法兰的变形行为及密封失效的判据变得尤为重要。
2 法兰结构的数值模拟和试验研究
2.1 试验概况
试验容器的筒体法兰内径φ204 mm,筒体厚度2 mm,试验法兰装置见图3,图中给出了法兰关键尺寸参数。
共进行7组法兰试验,分别研究改变法兰环厚度H、毂的长度h和法兰外径Do等法兰尺寸参数对法兰整体结构强度和刚度的影响。测量系统包括法兰关键点应变测量和水压实时监测,应变测点分为法兰环内侧环向、法兰环外侧环向、法兰筒体轴向和环向,具体测点如图4所示。其中,法兰环外侧和筒体测点使用量程为5%的国外应变片,其余测点使用国产应变片。
在不同几何尺寸下,法兰结构发生泄漏时的压力即最大承载能力,其越大认为法兰强度和刚度就越好。法兰由法兰环、毂、筒体三部分组成,其变形相互影响和制约,改变法兰某个尺寸,对法兰各部分的应力、应变的影响也不尽相同。从数值模拟结果来看,法兰最大应力多处于法兰环外侧的螺栓连接位置的下方(即法兰后毂与螺栓之间的区域),但此处做应变测量有很大困难,所以,选择法兰环上应变值表示改变法兰尺寸对法兰强度和刚度的影响。
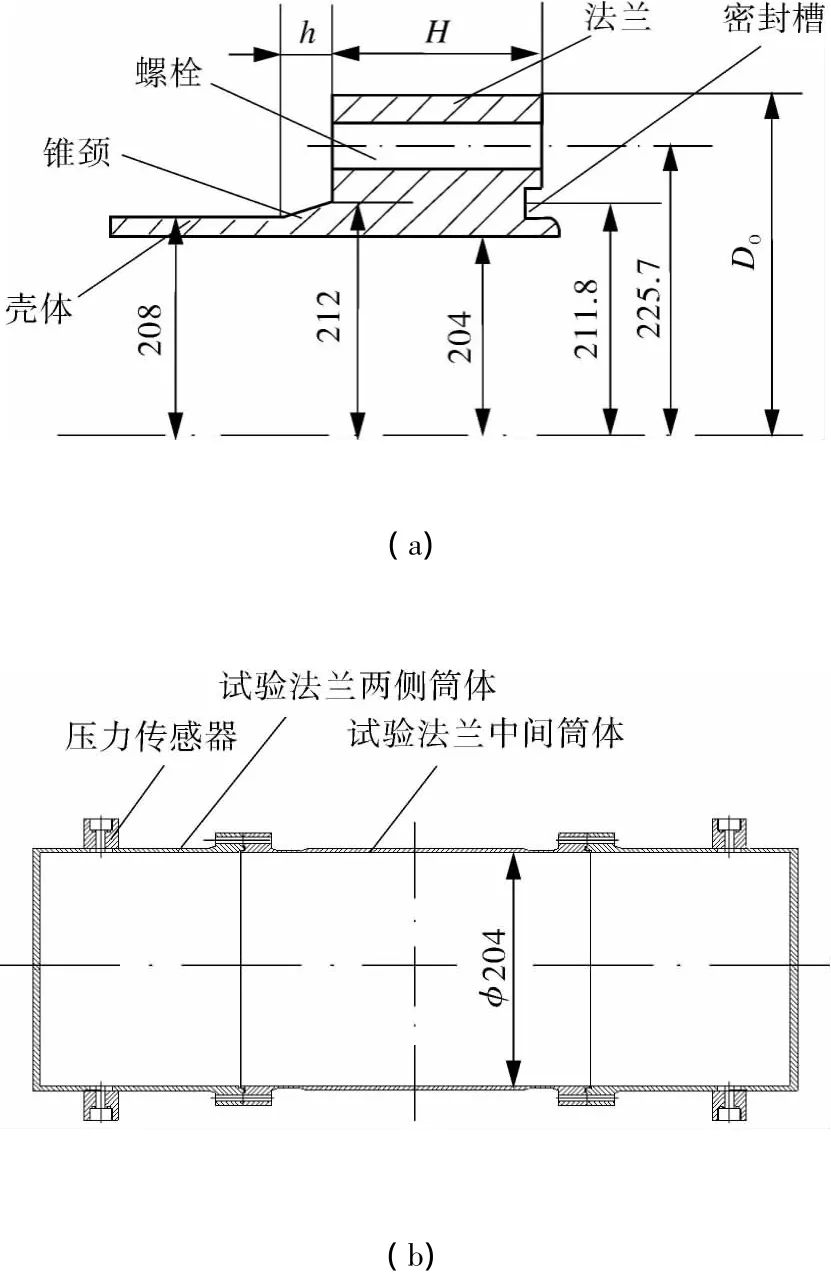
图3 试验法兰装置示意

图4 法兰连接系统的关键测点
2.2 数值模拟
利用ANSYS有限元分析软件,对法兰连接结构进行三维有限元计算,研究容器筒体发生塑性变形时法兰接头的变形,并给出详细的应力分析。法兰连接系统中,法兰、壳体为轴对称结构,45根螺栓沿法兰环均匀分布,螺栓直径φ5 mm,总体结构为周期性对称模型,取整体结构的1/45来构造计算模型,包角为2°,包含半个螺栓连接件。为了避免边界效应,根据圣维南原理[9],取连接法兰的壳体长度为200 mm,如图5所示。
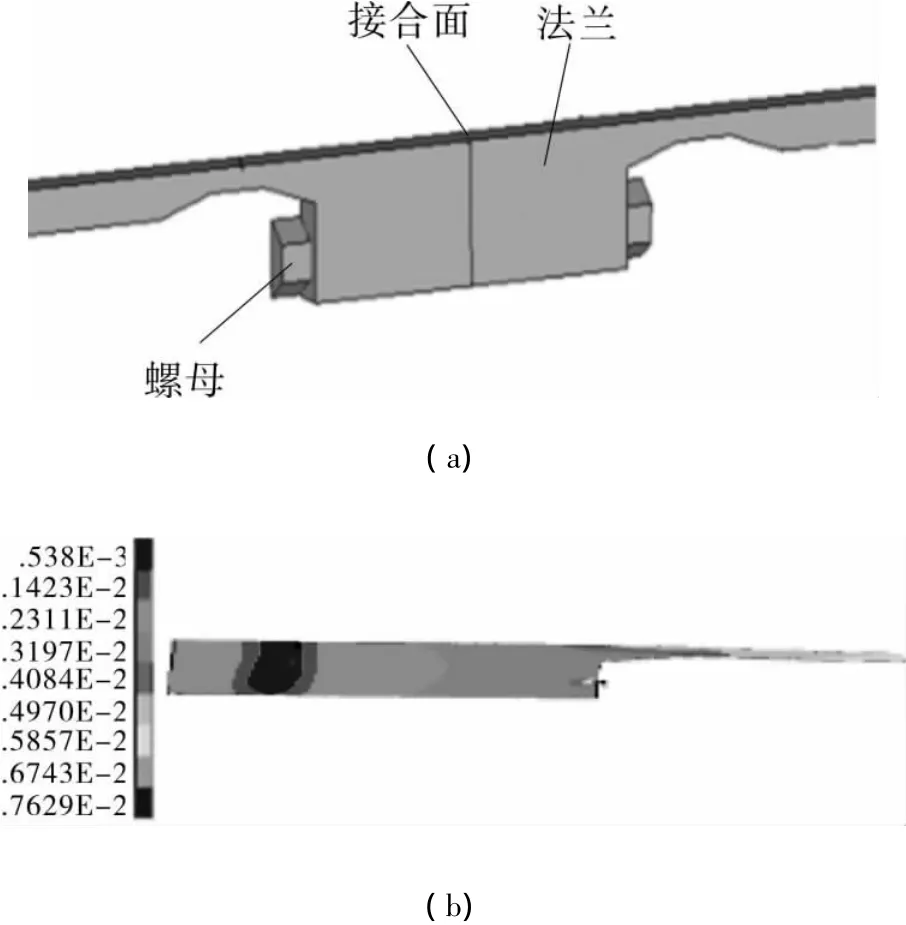
图5 法兰有限元模型和应力分布图(1/45部分)
材料本构关系选用双线性随动硬化模型,法兰、筒体材料弹性模量200 GPa,泊松比0.3,屈服应力345 MPa,切线模量8.6 GPa;螺栓弹性模量200 GPa,泊松比 0.3,屈服应力 900 MPa,切线模量 8.6 GPa。
载荷分为两部分:预紧载荷和工作载荷。
根据实际工作经验,螺栓的预紧应力取屈服应力的30%左右,螺栓的预紧载荷为预紧螺栓应力乘以螺栓横截面积,即:

式中 r——螺栓半径,mm
σ0——法兰材料的屈服强度,MPa
计算模型端部承受相应的由内压产生的轴向拉应力为:
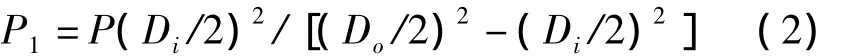
式中 P——法兰筒体承受压力,MPa
Di——法兰内径,mm,取 204 mm
Do——法兰壳体外径,mm,取 226 mm
在对称面上施加对称位移边界条件,为了避免刚性位移,一侧筒体端部约束轴向位移,螺母与法兰、两法兰接触面之间均建立接触对,摩擦系数取0.1。
2.3 改变法兰环厚度对法兰强度/刚度的影响
3组试验法兰环厚度分别为19 mm(结构1)、25 mm(结构2)、28 mm(结构3),法兰承受最大压力分别为7.9,9.8,12.1 MPa,即 3 种结构法兰发生泄漏的最大压力值。试验表明,随着法兰环厚度的增加法兰抵抗变形的能力增加。表1列出了改变法兰环厚度条件下的结果及对应条件下的数值模拟结果。

表1 改变法兰环厚度,法兰各点的实测应变平均值和数值计算结果的比较
从试验和数值模拟结果来看:随着法兰环厚度的增加,法兰环上的环向应变逐渐降低,法兰连接筒体部分的环向应变随之升高,说明随着法兰环厚度的增加,法兰环处越难失效,筒体处越容易失效;法兰环内侧、外侧环向应变方向不一致,在环中间区域将存在一个低应力区,这在数值模拟中也得到证实;螺栓孔上方的应变值要大于螺栓孔中间的应变值,说明螺栓孔对法兰局部的变形有很大影响。
2.4 改变毂的长度对法兰强度/刚度的影响
此组试验主要针对改变毂的长度参数。3组毂的长度分别为4 mm(结构1)、6 mm(结构2)、8 mm(结构3),法兰环厚度均为25 mm,法兰承受最大压力分别为 8.9,9.8,10.5 MPa。表 2 列出了改变毂的长度条件下的试验结果及对应的数值模拟结果。

表2 改变毂的长度时,法兰各点的实测应变平均值和数值计算结果的比较
从表2可以看出,当毂的长度增长时,法兰环上平均应变值有所降低,但降低程度有限,说明增加毂的长度有利于法兰强度的增加,但作用不大。法兰环偏转以毂作为转动支点,增加毂的长度对法兰转动产生抑制作用。
2.5 改变法兰外径对法兰强度/刚度的影响
此组试验主要针对改变法兰外径参数。3组法兰外径分别为238 mm(结构1)、241 mm(结构2)、244 mm(结构3),法兰承受最大压力分别为9.8,9.5,9.7 MPa。
表3列出了改变法兰外径条件下的试验结果及对应的数值模拟结果。
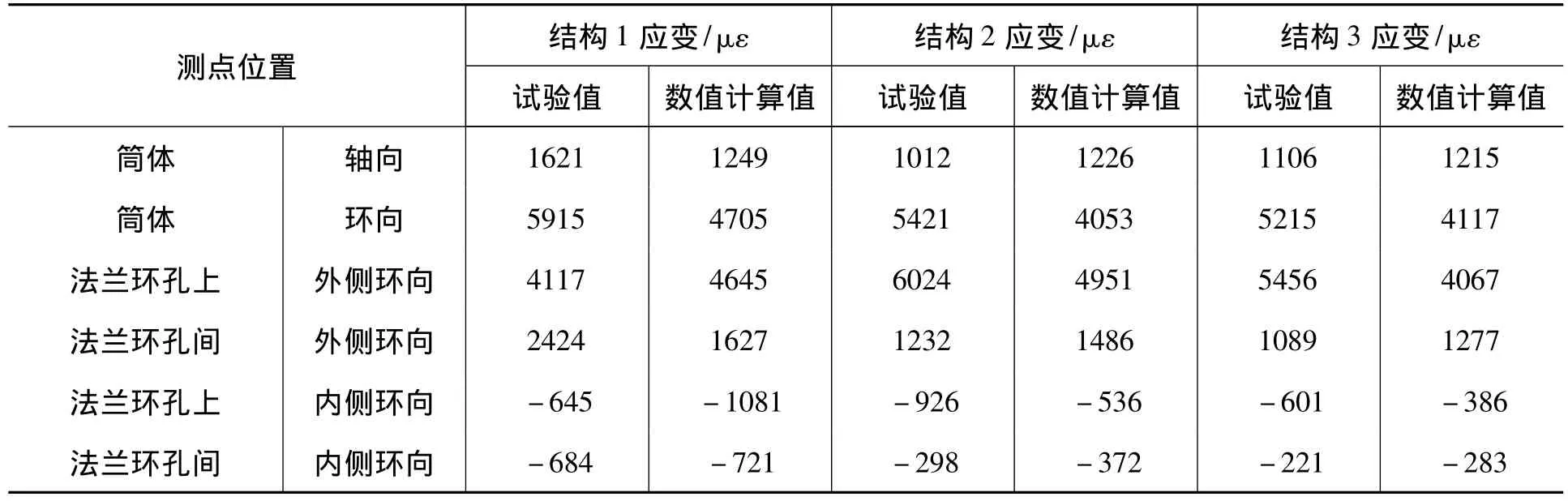
表3 法兰各关键点应变试验平均值和数值计算结果比较
从表3可以看出,当增大法兰外径时,法兰环上环向平均应变值有所降低,但降低幅度不大,说明增大法兰外径对法兰环环向应变有作用,但影响不大;3种外径的最大水压值相差不大,说明外径对法兰结构承载能力影响不大。由式(3)示出,法兰环截面承受的最大弯矩与法兰外径成正比,提高法兰外径会提高法兰刚度,但此时要求法兰环进入全截面塑性,而事实并非如此。从试验和数值模拟结果来看,法兰泄漏时法兰环内侧、外侧大多还处于弹性阶段。从弹性范围的法兰刚度计算可知,法兰外径增加反而会降低法兰刚度。所以,提高法兰外径对法兰刚度的影响不能一概而论,需要具体进行分析。法兰环截面具有塑性抗弯能力:

式中 b——法兰环厚度,mm,b=Do-Di
h——法兰长度,mm
在密封圈相同条件下,法兰外径241 mm和244 mm时,密封圈压缩量比法兰外径238 mm分别降低0.31%和0.52%,表明改变法兰外径对法兰转角的影响有限。在最大水压造成泄漏情况下,法兰外径为238,241,244 mm的法兰面内侧张开距离的数值模拟结果分别为0.86,0.81和0.82 mm。从结果来看,法兰外径对法兰环内侧张开距离影响不大,且变化不一致。
2.6 法兰环厚度、毂的长度和法兰外径对法兰变形的影响大小比较
改变法兰环厚度、毂的长度和法兰外径对法兰变形的影响大小,可以用厚度25 mm、毂的长度6 mm、法兰外径238 mm的法兰作为基准,其他尺寸的法兰结果与基准法兰变形的比值,来说明应变变化的大小。
表4,5列出了改变法兰尺寸,法兰关键点的应变变化率数据。

表4 改变法兰尺寸时,法兰关键点实测应变平均值的变化率
从表4,5可以看出,改变法兰环厚度、毂的长度和法兰外径对法兰各点应变都会产生影响。当尺寸增大时应变有降低趋势(变化率为负),反之,尺寸减小时应变增大(变化率为正);其中法兰环厚度对法兰各点的应变影响最大,改变法兰环厚度的变化率最大可达129%,改变毂的长度和法兰外径变化率则相对较小;当增大法兰尺寸时,法兰环部分的应变变化率呈负值,法兰筒体的应变变化率呈正值,说明法兰环应变值降低的同时法兰筒体的应变值则增大,反之亦然。同时,法兰结构各点的应变值大小以及其应变变化率与法兰内部介质压力有直接联系,一般,应变大小与压力呈正比关系。当法兰环厚度、毂的长度和法兰外径增加时,内部承载介质压力也提高,法兰环上环向应变降低,说明增加法兰尺寸对法兰环单向环向变形作用是积极的。
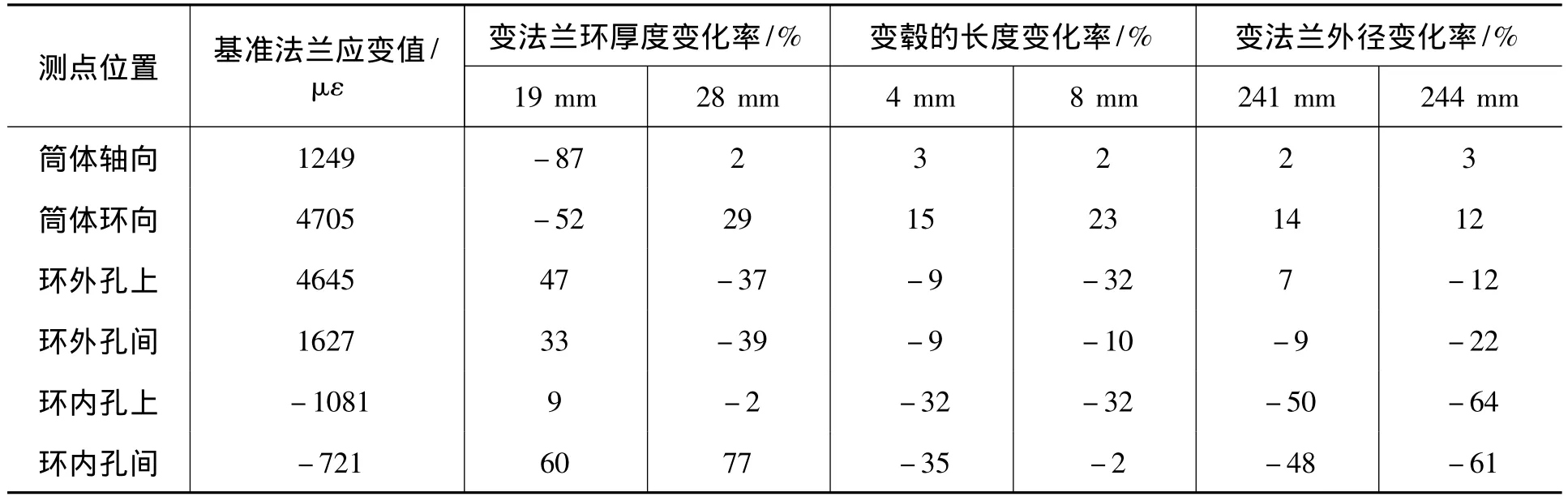
表5 改变法兰尺寸时,法兰关键点应变数值模拟结果的变化率
3 结论
利用静水压模拟爆炸准静态压力载荷对法兰进行了试验研究,根据应变和压力的测量对不同法兰关键尺寸条件下的法兰结构关键点应变进行了分析,并综合比较数值模拟和试验结果之间的差异及存在差异的原因。试验表明,增大法兰环厚度时,法兰的承载静压的能力显著提高;增大法兰毂的长度时,法兰的承载静压的能力变化不大,但也呈增长趋势;增大法兰外径时,法兰的承载静压的能力变化不大,而且增大法兰外径将对整个容器的总体最大外径尺寸产生直接的影响,这是不可取的。
综上所述,法兰发生泄漏是因为爆炸产生的气体压力,使法兰发生张开和偏转而导致密封面分离,而密封圈的回弹不足以补偿该分离量,或密封圈压缩量减少,使得密封比压下降,下一步将着重从法兰变形角度(与法兰的系统刚度有关)进行密封分析。
[1] 赵士达.爆炸容器[J].爆炸与冲击,1989,9(l):85-96.
[2] 朱文辉,薛鸿陆,韩钧万,等.爆炸容器动力学研究进展评述[J].力学进展,1996,26(l):68 -77.
[3] 胡八一,刘大敏,刘光祚,等.爆炸容器的研究及应用概况[J].爆轰波与冲击波,1998,23(3):1 -6.
[4] DUFFEY T A,ROMERO C.Strain Growth in Spherical Explosive Chambers Subjected to Internal Blast Loading[J].International Journal of Impact Engineering,2003,28:967 -983.
[5] 陈星,王凤英,吴玉平.圆柱形爆炸容器冲击载荷及其动力响应的数值模拟[J].压力容器,2012,29(3):17-21.
[6] TROTT T,STEVEN R R.Confinement Vessel Dynamic Analysis[R].LA -13628 - MS,1999:68.
[7] MURALI M,KRISHNA K,SHUN M S.A Study on the Sealing Performance of Bolted Flange Joints[J].Pressure Vessels and Piping,2007:349-357.
[8] SHELL C M,SWIFT R P,MARUSAK N L,et al.Response of Steel Vessels and Cavity Liners to Dynamic Loading[C].1993:487 -495.
[9] KRISHNA M M,SHUNMUGAM M S,PRASAD N S.A Study on the Sealing Performance of Bolted Flange Joints with Gaskets Using Finite Element Analysis[J].Pressure Vessels and Piping,2007,84(6):349-357.

