气瓶动态爆破压力预测

韦 晨，王泽军，谭 蔚，姜 斌

(1.天津市特种设备监督检验技术研究院，天津 300192;2.天津大学，天津 300072)

0 引言

焊接气瓶是用于充装液氨、液氯、环丙烷、液化石油气等低压液化气体和溶解乙炔气体的可重复充装而无绝热装置的移动式压力容器。其使用广泛、数量大、流动性大、管理分散、使用环境恶劣，充装介质大都具有易燃、易爆、剧毒、强腐蚀等性质［1］。所以，气瓶在为经济发展作出贡献的同时，也存在着一定的安全隐患。近年来，存在着超期未检气瓶、超期服役气瓶供应市场的情况，安全隐患非常突出，气瓶爆炸事故时有发生。

事故发生后，在分析事故原因过程中，需要对事故过程进行模拟，计算爆破压力。对于气瓶静态爆破压力的模拟研究较多，1957年，COOPER就发表了关于预测气瓶静态爆破压力的论文［2］，并提出一个解析方程来预测由各向同性塑性材料制成的钢瓶的静态爆炸压力，这个方程得到了理想的爆炸压力、材料属性、原始尺寸和材料极限抗拉强度的关系。随后，相继建立起基于弹性理论、弹塑性理论、塑性理论，适用于薄壁、厚壁、单层、多层，内、外壁存在腐蚀缺陷等不同条件下的气瓶静态爆破压力模型［3－6］。

静态爆破常用于模拟分析气瓶的水压或气压爆破，其爆破形式与气瓶爆炸还是有很大区别的。由于水压或气压爆破升压速度较缓慢，气瓶受载荷作用时间长，应变速率低，可以看作是静态或准静态过程。按照应变速率划分，当应变速率低于10－5s－1时称为静态变形;介于 10－5～ 10－3s－1时称为准静态变形;高于 10－3s－1时称为动态变形［7］。通常，随着应变速率的提高，材料的屈服强度和抗拉强度提高，延伸率降低，出现屈服滞后及断裂滞后等现象。要研究气瓶的爆炸过程，就需掌握气瓶材料相关的动态力学行为，因为相关动力学性能数据将为运用动力学模型对爆炸过程进行模拟提供更为准确的边界条件，提高模拟结果的精确性。

对于材料动态力学性能的研究多集中于航空、军工等领域，虽然也有对 20#钢［8－10］、爆炸容器［11－14］及意外撞击和冲击波作用下气瓶的动态响应［15］的研究，但还是缺少与气瓶爆炸相关的研究。文中以气瓶材料HP295钢为研究对象，通过力学试验研究其在动态加载条件下的力学性能，发现随应变速率增加，HP295钢的抗拉强度和屈服强度提高，说明HP295钢具有应变速率效应;建立有限元模型并结合得到的动态强度指标，对气瓶爆破进行动态分析，结果表明气瓶最终在筒体处发生破裂，随加载速率的增加，气瓶爆破时产生的塑性变形减小，应力增加，爆破时间减少，爆破压力增加;随加载速率的增加，有限元分析得到的爆破压力与使用修正后的巴洛公式估算得到的爆破压力逐渐接近，所以动态快速加载条件下，可用该公式对爆破压力进行预测。

1 试验及结果讨论

1.1 试验方法

将厚度为3.5 mm的HP295钢板加工成试样，如图1，2所示，对每个试样都进行编号，并测量其横截面积的实际尺寸。

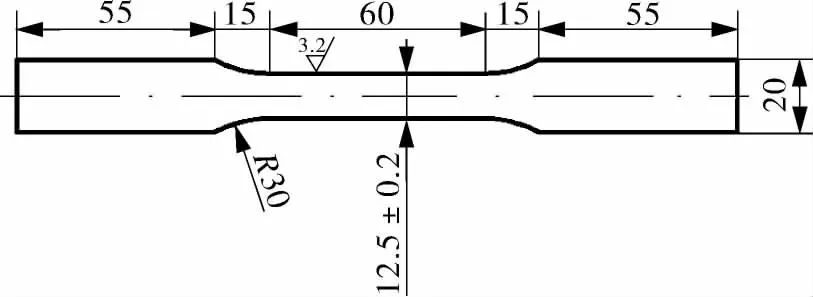
图1 试样几何尺寸

图2 加工后的编号试样

为研究HP295的应变率效应，将加工后的试样分组，分别进行如下试验:使用最大负荷为100 kN，型号为CSS－44100的电子万能试验机，其配有精度为0.02 mm的游标卡尺可准确定位，并装有引伸计，以0.05 mm/s的拉伸速率进行(准)静态拉伸试验;使用型号为ISPRON的电液伺服疲劳试验机，其配有精度为0.2 mm的游标卡尺可准确定位，由于拉伸速率较快，没有安装引伸计，分别以10，100和200 mm/s的拉伸速率进行动态试验。

1.2 试验结果及分析讨论

将每组试样的试验结果取平均值，应力—应变曲线如图3所示。将拉伸速率与应变速率及HP295各强度指标的对应关系列于表1。可以看出，随拉伸速率增加，弹性阶段历程变短，弹性极限、屈服强度、抗拉强度逐步增大;应变变化不规律，因为拉伸速率较快时，无法安装引伸计，所以导致应变测量不精确，但从趋势看，当拉伸速率达到200 mm/s时，曲线的颈缩阶段历程变短。

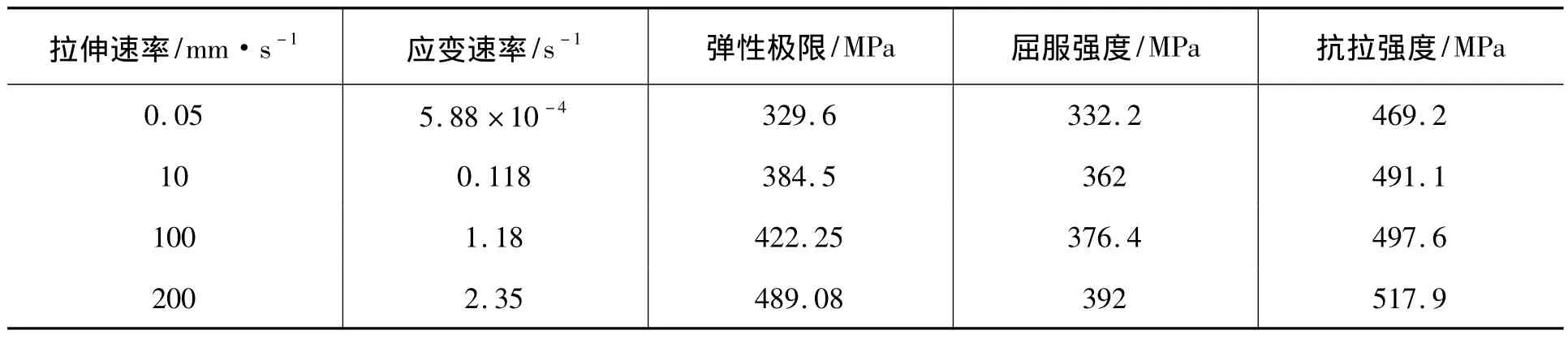
表1 拉伸速率与应变速率及HP295各强度指标的对应关系

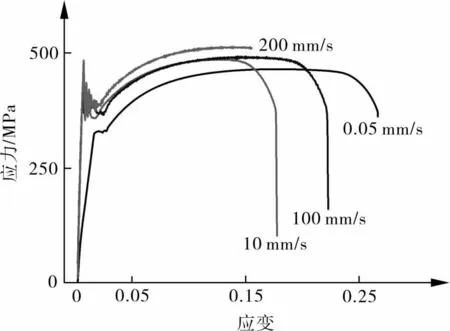
图3 HP295在各拉伸速率下的应力—应变曲线

总之，随着加载速率的增大，弹性极限呈单调递增趋势，屈服强度和抗拉强度逐步增加，且增势趋缓。说明HP295具有应变率效应，且随拉伸速率的增加，HP295的应变率效应越不明显。

2 有限元模拟及爆破压力预测

2.1 建模

针对118 L液化石油气瓶(直径400 mm，壁厚3.5 mm)进行模拟。由于在爆炸案例中，一般爆破位置位于筒体部分，所以对筒体部分重点模拟，为了简化模型，将上封头处气阀忽略考虑，气瓶外围的防震圈以及气瓶裙座对本模拟影响不大，可以忽略。由于气瓶几何形状和载荷都是轴对称的，为了建模方便选择建立二维轴对称模型，并取气瓶的1/4进行建模。使用ANSYS软件，选用二维8节点实体结构单元Plane 183划分网格，本模型只考虑对称面上的对称约束，即限定X对称面上Y方向上的位移约束以及限定Y对称面上X方向上的位移约束，如图4所示。

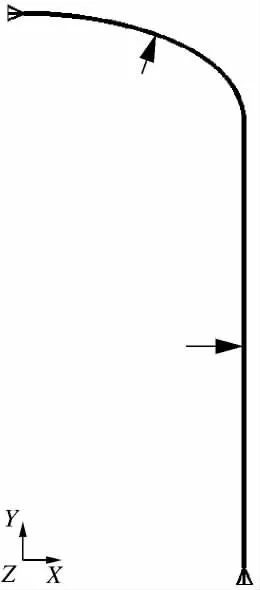
图4 气瓶有限元模型

对于材料属性的定义和输入，由于拉伸速率较大，试验时无法用引伸计进行测量，所以由曲线得到各拉伸速率下的弹性模量是不准确的。考虑到拉伸速率对于金属的弹性模量影响较小，这里统一取200 GPa，泊松比取0.3，在多重各项同性选项中输入应力应变。其中对于大应变塑性分析，使用对数(Hencky)应变即真实应变、Cauchy应力即真实应力，应力应变数据以真应力—对数应变形式给出。

比较应力应变与真实应力应变的区别可知，从试样发生塑性应变开始，真实应力要比实际应力中大，这是因为试样发生塑性变形时，试样横截面积发生了变化(逐渐变小)，所以实际的应力要大于工程应力。

文中旨在考察气瓶的动态力学响应，采用多个载荷步多个时间子步的加载方式，在气瓶内表面施加压力，压力的大小根据不同的加载速率，逐步增加加载时间进行调试。加载速率由拉伸速率换算得到，根据试验数据记录，用最大载荷除以最大载荷出现的时间以及试样横截面尺寸，得到加载速率后，以每2 MPa为一载荷步，每一载荷步中时间子步设为1000(通过多次调试，减小每一载荷步的压力增量及增加时间子步，对结果影响不大)，逐步增加加载时间，直至气瓶爆破。

采用时间历程后处理器(POST26)和通用后处理器(POST1)进行结果分析和处理，通过改变材料属性，对比相同有限元模型、不同加载速率的结果，并得出结论。在0.05，10，100和200 mm/s这4个拉伸速率下进行模拟，通过换算将拉伸速率与加载速率的对应关系列于表2。其中0.05 mm/s的拉伸速率较慢，对应的1.532 MPa/s的加载速率应属于准静态爆破的加载速率，其他3个加载速率对应于动态爆破。

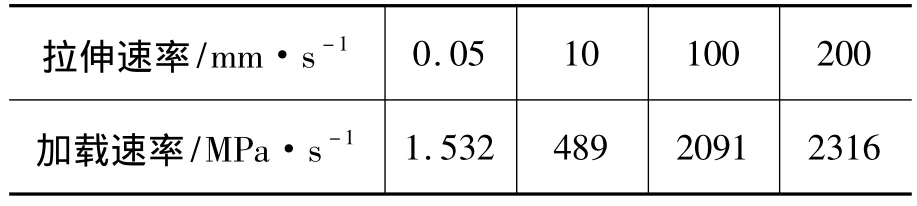
表2 拉伸速率与加载速率的对应关系

2.2 不同加载速率对气瓶爆破后应力应变的影响

计算结束后，得到了气瓶在不同加载速率下，失效时模型所受应力及发生的塑性应变(如图5，6所示)，通过分析应力状态可知封头和筒体均受力，其中所受最大应力出现在筒体近X轴处，且所受最大应力的大小随加载速率的增大而增加(由543 MPa增加到583 MPa)，见表3。

图5 不同加载速率下爆破时模型各处的应力水平

由于当模型中的单元塑性变形超过一定限度后，计算自动停止，所以不同加载速率下爆破的气瓶的宏观塑性变形形状没有大的变化，但封头和筒体均发生变形，结合图6可以看出，在不同加载速率下，筒体处应变均最大，最终失效应发生在筒体处。

虽然气瓶爆破后形状变化不大，但从图6可以看出，不同加载速率下塑性变形量发生改变，随加载速率的增加，气瓶爆破时产生的塑性变形减小(由 0.1448 减小到 0.1183，见表 3)。实际情况，随着加载速率的增加，气瓶变形的响应时间减少，材料组织中的位错等缺陷迅速聚集，材料性能由韧性向脆性逐步转变，塑性变形逐渐减小，所以模拟结果与实际情况相符合。

图6 不同加载速率下爆破时模型发生的塑性应变

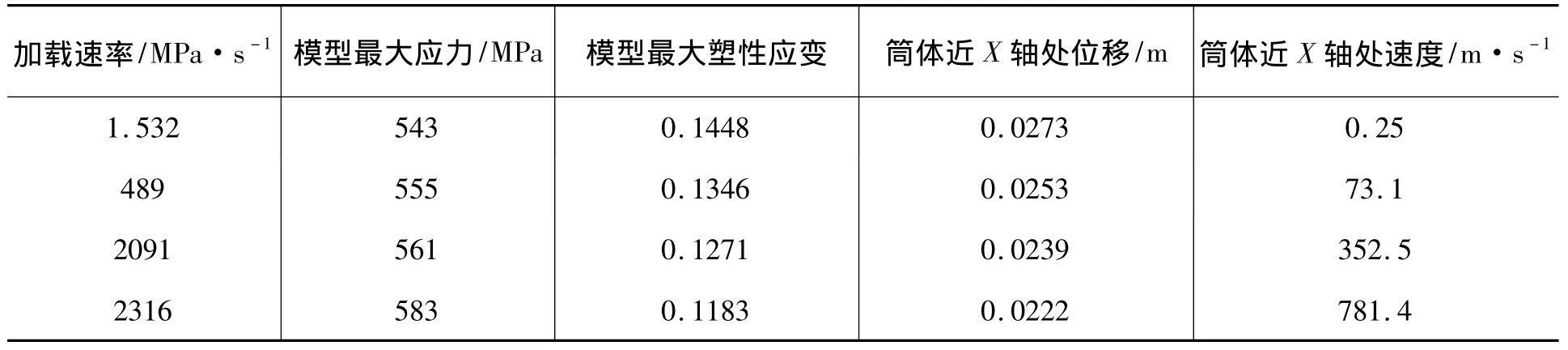
表3 不同加载速率下气瓶爆破时的相关参数

另外，由于X方向的变形最大，比较不同加载速率下爆破时模型X方向发生的位移及X方向的速率，发现:爆破时模型X方向发生的位移随加载速率的增加逐渐减小(从0.0273 m减小到0.0222 m，如表3所示)，这与塑性变形的变化相一致。爆破时模型X方向的速率随加载速率的增加而增大(从0.25 m/s增大到781.4 m/s，如表3所示)。由此看出，加载速率从1.532 MPa/s增至2316 MPa/s，是由准静态爆破逐步过渡到动态爆破。

综上所述，通过不同加载速率下对模型应力及塑性应变变化的分析，发现其改变的趋势符合应变率效应。

2.3 不同加载速率对爆破压力的影响

通过上节分析，可知筒体近X轴处塑性应变及应力最大，选取该处单元，比较在不同加载速率下，塑性应变及应力随时间的变化关系，如图7，8所示。

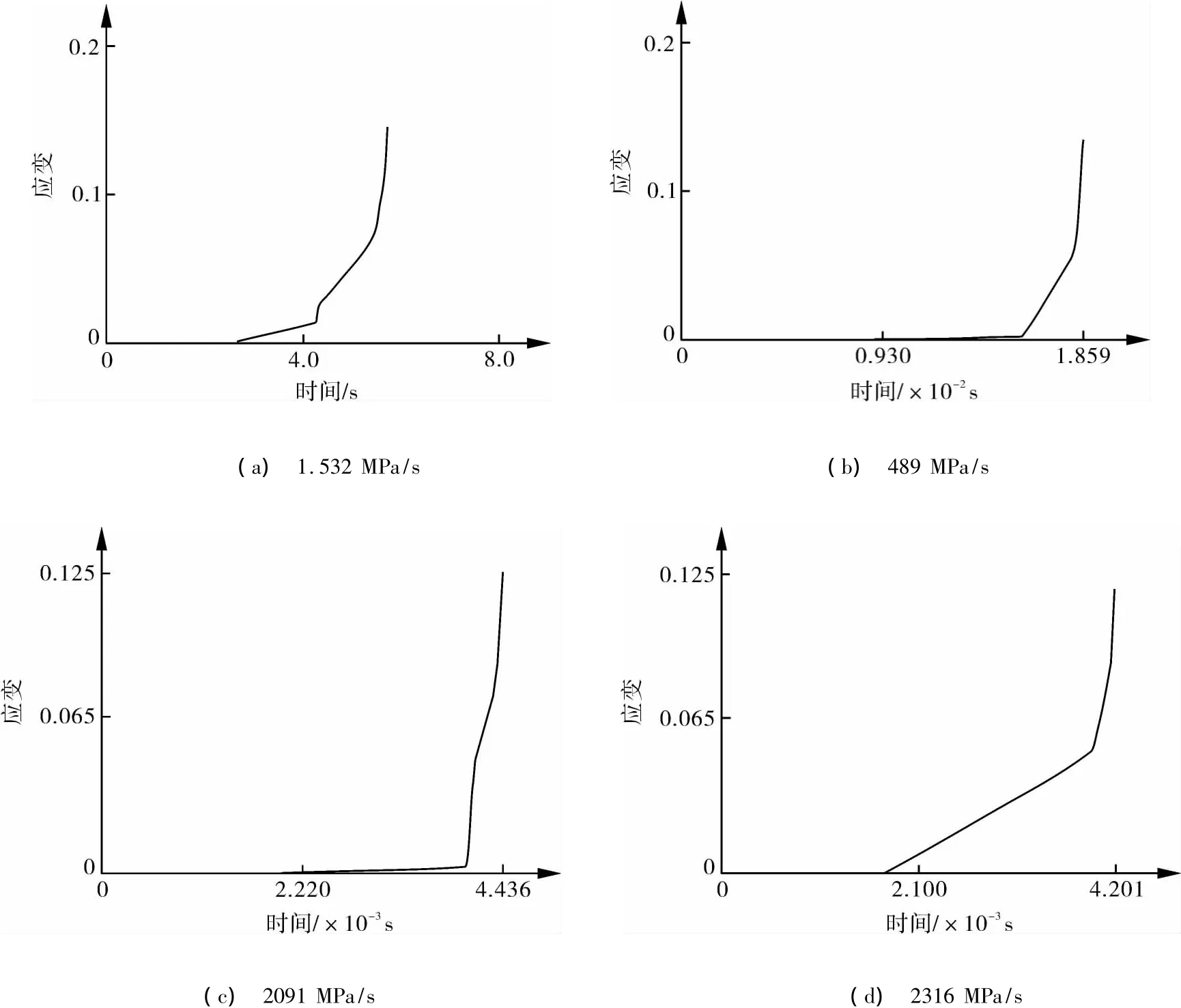
图7 不同加载速率下筒体近X轴处塑性应变与时间的变化关系

由图7，8可以看出，在各个加载速率下，模拟起始阶段塑性应变数值为零，应力随时间线性变化，说明起始阶段模型处于弹性变形阶段;一段时间后塑性应变曲线才开始出现，应力曲线斜率发生改变，筒体进入塑性变形阶段;当模拟时间终止时，筒体近X轴处的塑性应变及应力随时间变化的曲线斜率接近于无穷大，即只要时间增加，塑性应变和应力将增加无穷大，进一步证实了最终失效发生在筒体处。

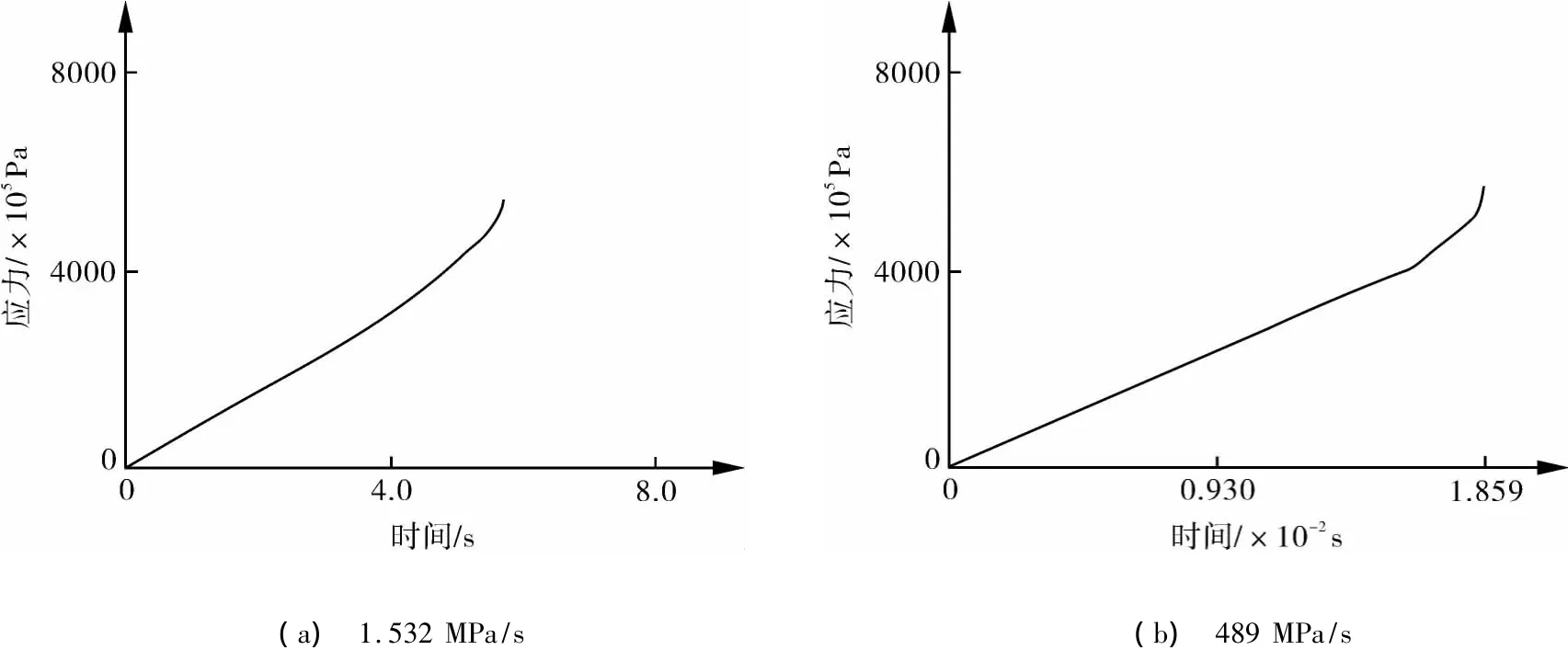
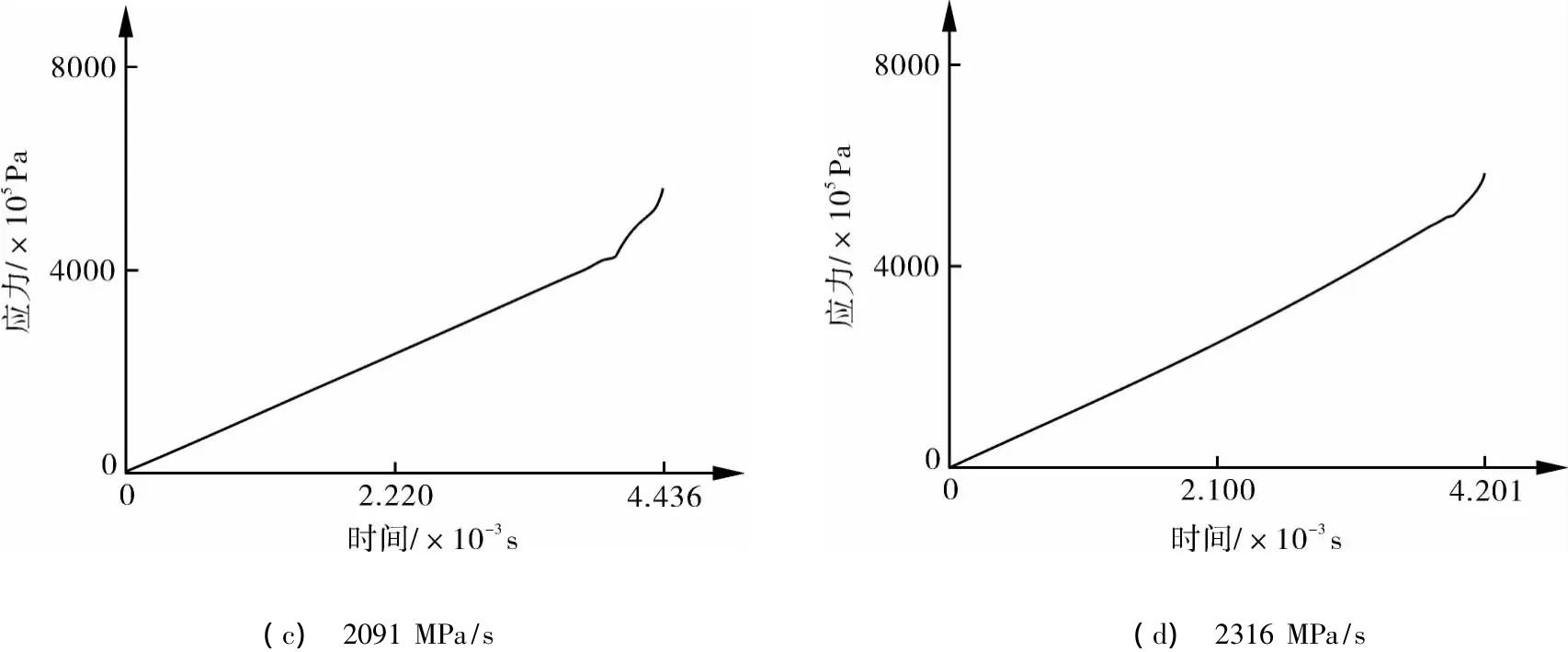
图8 不同加载速率下筒体近X轴处应力与时间的变化关系

由于计算无法继续，则取计算终止的时间为模拟爆破时间，模拟爆破时间与加载速率的乘积就是模拟爆破压力(如表4所示)。可以看出，随加载速率的增大，模拟爆破时间减少，模拟爆破压力增加。

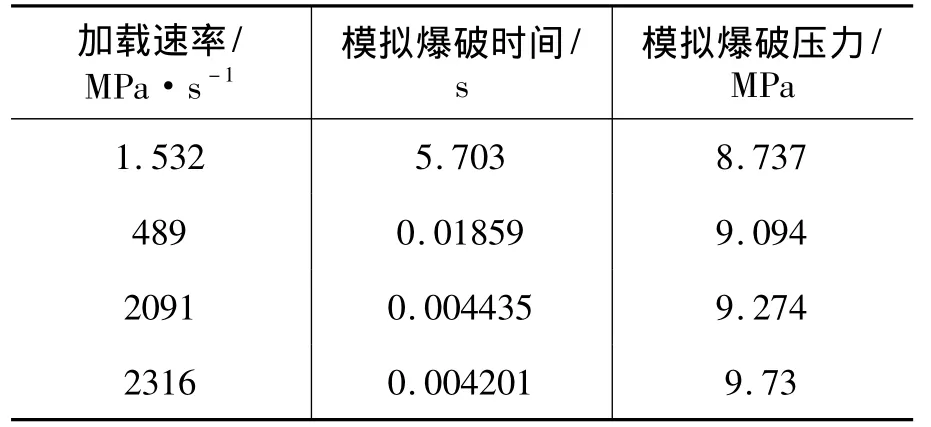
表4 不同加载速率下气瓶的模拟爆破时间及爆破压力

3 爆破压力模拟结果与经验公式计算结果对比

目前，较为常用的计算爆破压力的经验公式为Barlow(巴洛)公式:

式中 Pb——爆破压力

σu——极限强度，即抗拉强度

T——气瓶壁厚

OD——气瓶的外径

σu为静态拉伸试验得出的抗拉强度，与动态的抗拉强度有一定的关系:

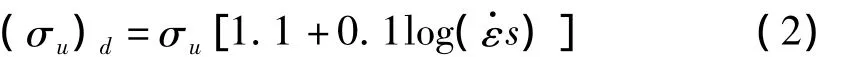
式中 (σu)d——动态的抗拉强度

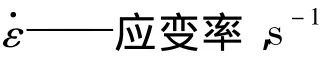
式中s代表单位时间。

故动态爆破压力可以表示为:

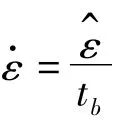
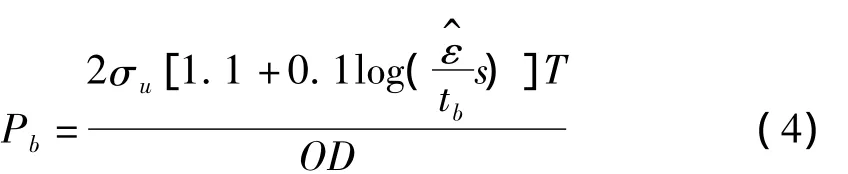
将由试验测得的静态抗拉强度、由模拟分析得到的最大的塑性应变及加载时间等数据代入式(4)，可得到不同加载速率下的爆破压力(如表5所示)，其中在快速加载条件下，模拟得到的爆破压力与计算得到的结果相差不大。

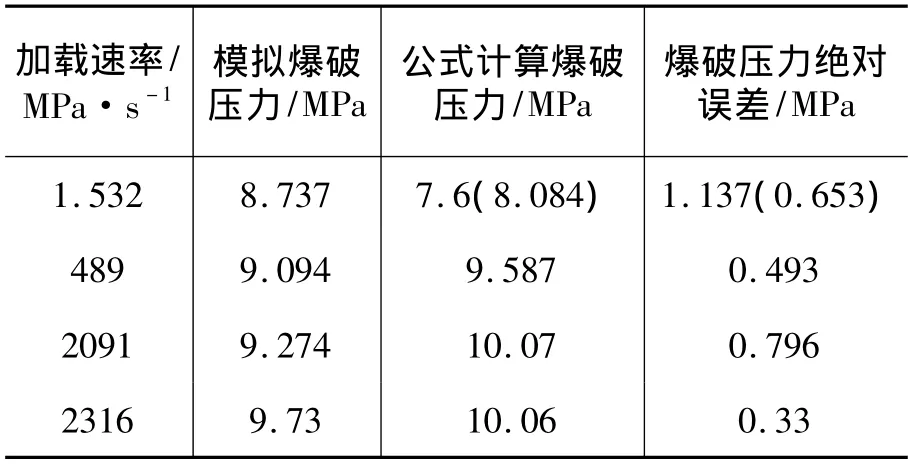
表5 不同加载速率下气瓶的模拟爆破压力与计算爆破压力

然而在1.532 MPa/s的加载速率下，二者结果相差较大，因为1.532 MPa/s的加载速率处于静态加载范围，应使用式(1)进行估算，结果如表5中括号内数值所示，二者差值减小。

若使用表1中的强度指标代入式(1)计算，得到的结果与表5中的结果相差较大，因为表1中的数据是由工程应力—应变曲线得到的，而不是由真应力—应变曲线得到的。

综上，在动态快速加载条件下，有限元分析得到的爆破压力与经验公式估算得到的爆破压力很接近，可以使用修正的巴洛公式(式(4))对爆破压力进行预测。

4 结论

通过试验获得HP295钢的材料性能数据，代入有限元模型，使用ANSYS软件进行模拟，对不同加载速率下的气瓶爆破压力进行了预测，并与修正后的经验公式计算得到的结果进行对比，得到以下结论:

(1)随着拉伸速率增加(从 0.05到 200 mm/s)，HP295钢的抗拉强度和屈服强度提高(从469.2 到517.9 MPa，从332.2 到 392 MPa)，说明HP295钢具有应变率效应。

(2)有限元气瓶爆破动态模拟分析结果表明，对气瓶加载，筒体和封头都发生变形，最终在筒体处发生破裂。随加载速率的增加，气瓶爆破时产生的塑性变形减小，应力增加，爆破时间减少，爆破压力增加。

(3)随加载速率的增加，有限元模拟分析得到的爆破压力与使用修正后的巴洛公式估算得到的爆破压力逐渐接近，所以动态快速加载条件下，可用该公式对爆破压力进行预测。

［1］ 强天鹏.压力容器检验［M］.北京:新华出版社，2008:411.

［2］ COOPER W E.The Significance of the Tensile Test to Pressure Vessel Design［J］.Welding Research Supplement，1957，36(1):49 －56.

［3］ SVENSSON N L.Burst Pressure of Cylindrical and Spherical Vessels［J］.ASME Journal of Applied Mechanics，1958，25(1):89 －96.

［4］ TADMOR E B，DURBAN D.Plastic Deformation and Burst of Pressurized Multilayered Cylinders［J］.Journal of Pressure Vessel Technology，1995，117(1):85－91.

［5］ RAJAN K M，DESHPANDE U P，NARASIMHAN K.Experimental Studies on Bursting Pressure of Thinwalled Flow Formed Pressure Vessels［J］.Journal of Materials Processing Technology，2002，125 －126:228－234.

［6］ KLEVER F J.Burst Strength of Corroded Pipe:Flow Stress Revisited［C］//Proceedings of the 24th Annual Offshore Technology Conference.Houston:TX，1992，May 4－7:417－431.

［7］ MEYERS M A.［美国］.材料的动力学行为［M］.北京:国防工业出版社，2006:207－208.

［8］ CHENG Cunjiang，WIDERA G E O.Dynamic Burst Pressure Simulation of Cylindrical Shells［J］.Journal of Pressure Vessel Technology，2009，131(6):1 －11.

［9］ CHENG Cunjiang，WIDERA G E O.Development of a Simplified Theoretical Model for Dynamic Burst Time and Pressure of a Cylindrical Shell［J］.The Open O-cean Engineering Journal，2009，2:1 －6.

［10］ 郭昭亮，刘仓理，汤铁钢.预置圆孔膨胀环动态断裂行为研究［J］.实验力学，2010，25(5):546－552.

［11］ 赵福松，田锦邦，赵子龙.柱形爆炸容器动力响应的数值模拟［J］.中北大学学报，2010，31(4):356－359.

［12］ 陈星，王凤英，吴玉平.圆柱形爆炸容器冲击载荷及其动力响应的数值模拟［J］.压力容器，2012，29(3):17－21.

［13］ DENG Guide，XU Ping，ZHENG Jinyang，et al.Numerical Simulation of Blast Loading on a Thickwalled Cylindrical Vessel［C］//Proceedings of 2007 ASME Pressure Vessels and Piping Division Conference.San Antonio:ASME，2008:195 －198.

［14］ 马圆圆，郑津洋，陈勇军，等.椭圆封头圆柱形爆炸容器动力响应的数值模拟［J］.爆炸与冲击，2009，29(3):249－254.

［15］ 李海斌，赵长生，阳建红，等.意外撞击和冲击波作用下气瓶的动态响应［J］.压力容器，2009，26(5):32－37.