基于元胞自动机的结伴过街行人流建模与仿真

任 刚，丁晨滋，陆丽丽，于 晨，姚梦佳

（东南大学 江苏省城市智能交通重点实验室，南京 210096）

1 引 言

元胞自动机（Cellular Automata，CA）目前已被广泛应用在交通流的研究当中.元胞自动机最初是人工生命的研究方法和工具，由于CA结构简单、易于计算机编程实现等特点，基于CA的行人交通流研究也已成为热点：C Burstedde等[1]建立了场域模型；Victor J Blue等[2]提出两步骤并行更新模型；岳昊等[3,4]提出动态参数模型.但目前针对过街情形的行人交通流微观仿真还缺少全面深入的研究成果：LI Xiang[5]利用场域模型对行人过街交通流进行了仿真研究，模型针对行人过街的环境进行了合理的设置；丁宁[6]利用动态参数模型对行人过街交通流进行了研究，模型中考虑了行人的从众心理.这些研究中都没有关注行人结伴行为对过街交通流的影响，而根据调查数据，在城市步行交通中有超过60%的行人处于结伴状态[7]，行人结伴行为对过街交通流的影响不可忽视.

本文利用元胞自动机建立考虑行人结伴行为的行人过街模型，模型主要根据动态参数模型[3，4]的建模思想，通过设计阻力参数、方向参数、空格参数、从众参数和结伴参数，来反映行人在过街中心理安全空间、前进、避让换道、从众心理和结伴行为等行走特性，并通过控制过街行人总数、结伴行人所占比例及结伴群体结构对模型进行仿真分析，以研究结伴过街行为对整体过街行人流的影响机理.

2 建模

2.1 场景设置

模型中人行横道离散化为L×W个元胞，其中L为人行横道的长度，W为人行横道的宽度，单个元胞的尺寸设为0.4×0.4 m2.因为行人经常移动到人行横道画线部分外面，所以模型中人行横道两侧各向外延伸L×w个元胞作为可移动空间，同时人行横道左右两端各向外延伸l（W+2w）个元胞作为行人等候区.即整个行人过街的环境为（L+2l）·（W+2w）的二维离散系统，系统两边界为封闭性边界，行人不能越过，如图1所示.

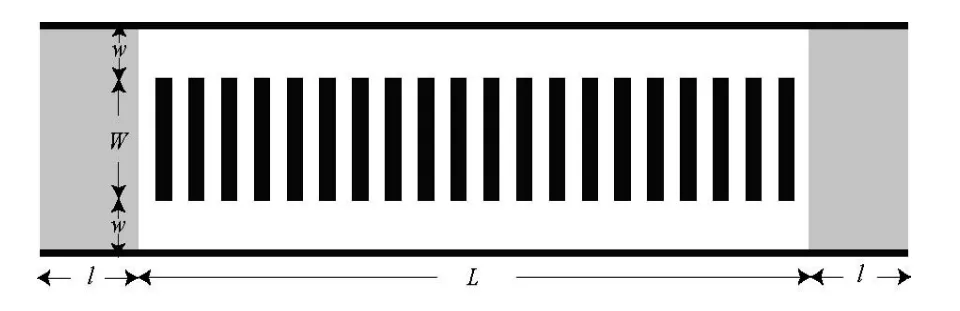
图1 模型过街环境示意图Fig.1 Sketch of the crosswalk under consideration

模型中具有个体过街行人和结伴过街行人两种类型，行人的移动过程离散化为等长的时间步，行人每个时间步最多可以移动一个元胞的位置，即Vmax=1元胞/step.行人可以选择前进、左右平移或原地等待，由于在实际观测中，过街行人几乎不会出现后退的现象，所以模型中不考虑后退行为，则行人移动邻域如图2所示（以右行行人为例）.

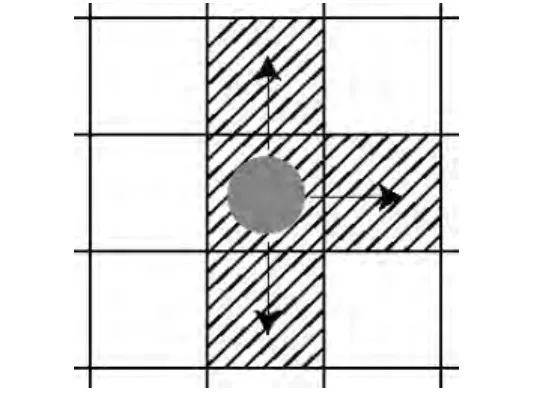
图2 行人移动邻域Fig.2 Movable neighbor cells for pedestrian

2.2 参数定义

在模型每个时间步长中，行人首先计算阻力参数R，根据前方拥挤程度判断该时间步是原地等待还是继续行走；如果继续行走，则行人根据目标元胞ij的方向参数Dij、空格参数Eij、从众参数Cij和结伴参数Gij的参数值来确定移动收益，并根据各个目标元胞的移动收益选择最终移动目标，其中i，j为元胞在系统中的坐标.

在计算阻力参数R和从众参数Cij时，需要确定行人的视野范围，本文选定的视野范围为3×5元胞的范围，如图3所示.

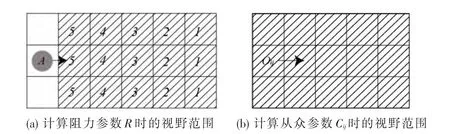
图3 计算阻力参数R和从众参数Cij时的视野范围Fig.3 The vision-conscious field for pedestrian used in the computation of R and Cij

(1)阻力参数R.

由于行人行走时存在一定心理安全空间[8]，在过街情形中前方其他行人会对行人产生明显的阻力作用，当前方人群较拥挤时，行人会降低步速以与拥挤人群保持一定的距离.模型中利用阻力参数R来反映这一特征，在计算阻力参数R时，行人A建立所处元胞前方3×5的视野领域，考虑到前方其他人对行人产生的阻力作用受距离影响比较明显（离该行人越近的其他行人对其产生的阻力越大），所以计算阻力参数R时，对视野领域内的元胞按与行人A的距离给出不同的影响权重p，距离行人A最近的一排元胞影响权重p设为5，并根据距离逐渐衰减，直至视野领域中距离行人A最远的一排元胞影响权重p设为1（如图3（a））.据此，阻力参数R的值为

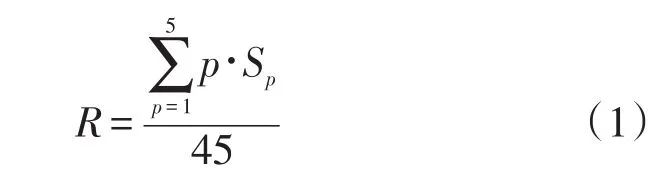
式中 p为视野领域中元胞的阻力影响权重值；SP为影响权重值为p的所有元胞上占据的行人数.

行人将以（100×R）%的概率受到前方行人的阻力影响而降低步速，即该时间步选择原地等待.

(2)方向参数Dij.

行人的行走具有一定的方向性和目的性，行人移动到前进方向正前方的元胞时，其与目的地在前进方向上的距离更加接近，因此行人前进方向正前方元胞Dij取1；当行人向正前方移动受阻时,行人会选择左、右平移或者原地等待，以期下一时间步能够实现前进方向上的移动，所以行人至少需要两个时间步才能够实现在前进方向上1个元胞的收益，因此行人左、右平移或原地等待的目标元胞Dij为0.5.

(3)空格参数Eij.

行人在移动过程中，会避开已经被其他行人占据的位置，而选择空格的位置作为下一步的移动目标.因此处于空格状态的元胞Eij为1，表示空格位置对行人的选择具有最大的吸引作用；处于被占据状态的元胞Eij为-1，表示被其他行人占据的位置会对行人的选择产生最大的排斥作用；移动邻域中心位置元胞被行人自身占据，但行人可以选择原地等待，因此Eij取1.

(4)从众参数Cij.

行人在过街的移动过程中，会体现出一定的从众心理作用[9]，具体表现为行人会一定程度地跟随同向的行人群，而避开对向的行人群.模型中用从众参数Cij来反映这一特征.在计算从众参数Cij时，行人A在目标位置Oij前方建立3×5的视野领域（如图3（b）），并判断视野领域内同向、对向移动的行人数及空格元胞数，从众参数矩阵元素的值为

式中 S1为视野范围内与行人A同向的行人数和空格元胞数之和；S2为视野范围内与行人A移动方向对向的行人数.

(5)结伴参数Gij.

处于结伴状态的行人在过街过程中，会尽量保持与其结伴同伴在位置关系上的维系，模型中用结伴参数Gij反映这种特性.

处于结伴状态的行人拥有变量g，g是结伴群的序列号（g=0,1,2,…），不同结伴群的g值不同，属于同一个结伴群的行人都拥有相同的g值.行人A在计算移动邻域内每个元胞的结伴参数Gij时，通过匹配g值来寻找自己的结伴同伴，系统中每存在一个具有相同g值的其他行人，则Gij加上1/dn（dn为行人A的第n个结伴同伴与目标元胞的距离，计算见公式（4）），最终Gij的计算公式为

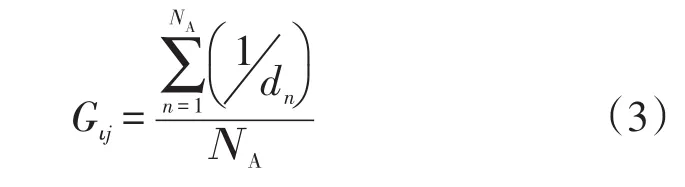
式中 ΝA为行人A的结伴同伴数，若A属于两人结伴，则ΝA=1；若A属于三人结伴，则ΝA=2，以此类推.

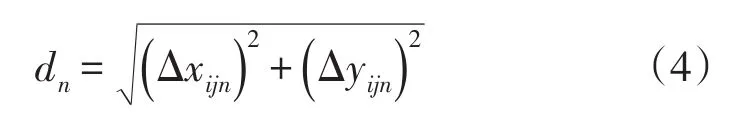
式中 Δxijn、Δyijn为元胞ij与行人A的第n个结伴同伴所处元胞的坐标差.

2.3 模型演化规则

行人根据计算目标元胞的各类参数值确定移动收益以选择移动目标，其中个体过街行人的结伴参数值Gij都计为0.模型假设两个方向过街行人群的人数、组成相同，N表示一个方向的过街行人数，n1表示个体行人数占N的比例，n2表示两人结伴行人数占N的比例，n3表示三人结伴行人数占N的比例.

模型在初始化中，会在等候区随机位置生成行人，但是处于同一结伴群的行人会保持并排紧靠在一起.仿真开始时，处于等候区的行人通过计算各个参数值来选择移动目标，此时邻近人行横道的行人会率先进入人行横道，而靠后的行人会因为阻力参数的作用有一定程度的滞留，但等候区及人行横道中的行人是遵循同一更新规则确定前进行为的.系统中行人经过人行横道到达对面等候区的一刻即已完成过街，但此时该行人仍对身后行人存在影响，因此不会被从系统中清除，行人继续行走越过系统左右边界时才会从系统中清除而不再更新状态，即系统左右边界为非周期性边界.每个行人拥有变量Yn来反映行人是否已经完成过街，初始各个行人Yn=0，表示未完成过街；当行人完成过街进入对面等候区时令该行人Yn=1，表示完成过街.模型按照如下步骤更新状态：

(1)对模型进行初始化，根据给定的N，n1，n2，n3在过街等候区生成行人，给结伴行人按所属结伴群分配g值，并初始化t=0.

(2)仿真开始，在时间步t内完成以下步骤：

①n为所有行人编号，n初始为1.

②若行人n已清除则跳至步骤⑤；否则继续步骤③.

③ 计算行人n阻力参数R，并以（100×R）%概率原地等待.若选择原地等待，则跳至步骤⑤；否则继续步骤④.

④行人n根据参数值计算邻域内各个元胞ij的移动收益Pij，行人n选择Pij值最大的元胞作为移动目标，如果移动邻域内有多个元胞拥有相同的最大Pij，则随机选择其中一个作为移动目标.Pij的计算公式为

式中 α、β、γ为权重系数，都大于等于0，且α+β+γ=1.

⑤令n=n+1，如果此时n≤2N，则返回步骤②；否则继续步骤⑥.

⑥如果有多个行人同时选择一个元胞作为移动目标，则随机选择其中一个行人将该元胞作为移动目标，其余行人则保持原位置.

⑦所有行人移动到移动目标，根据行人位置更新Yn值，并判断行人是否被清除，继续步骤(3).

(3)令t=t+1，若存在行人Yn=0，则返回步骤(2)；否则仿真结束.

3 仿真结果及分析

在仿真研究中，系统L=60，l=10，W=10，w=5，即人行横道长24 m，宽4 m，行人移动的有效宽度为8 m，一侧的行人等候区长4 m，宽4 m.行人步速设为1.2 m/s，而每个元胞边长0.4 m，即系统一个时间步t相当于1/3 s.结伴行人群按照结伴群结构可以分为两人结伴、三人结伴、四人结伴等，模型中结伴行人群只考虑两人结伴行人和三人结伴行人两种情形.为重点研究结伴行为特性，仿真分析中模型权重系数取α=0.25，β=0.25，γ=0.5.

3.1 过街行人流宏观特征

图4显示的是单方向过街行人数N=90，n1=1/3，n2=1/3，n3=1/3时不同时间步下过街行人流分布情况，即左行和右行过街行人都为90人，且个体行人为30人，处于两人结伴状态的行人为30人，处于三人结伴状态的行人为30人，系统总人数2N=180.由图中可见不同时间步的行人交通流特征如下：

(1)t=0时，系统在等候区生成行人，仿真开始到t=40时，对向行人流还没有相遇，行人不会受到对向行人的干扰，因此平均速度较快；

(2)从t=40到t=80这段时间，两个方向行人流开始交织，此时行人的平均速度急剧降低，整个过街过程中平均速度的最低值就出现在这个时段内；

(3)t=80时两个方向的行人流开始发生分层现象；

(4)t=120时对向行人流的分层现象已经比较明显，可以很清晰的看到两个方向行人流自发分成了4个通道；

(5)t=160时，两个方向行人流交织已经大多消散，且分层现象明显，所以此时平均速度已经基本稳定，直到t=200这段时间平均速度都比较平稳，只有少量提升.

图4 不同时间步t的过街行人流空间图Fig.4 Images representing the pedestrian flow distribution of the simulation taken at different time steps

3.2 结伴行人平均速度

为研究结伴行人行走特性，在N=90时，分三种情形：（1）n1=1，n2=0，n3=0；（2）n1=0，n2=1，n3=0；（3）n1=0，n2=0，n3=1.仿真输出三种情形下系统平均速度v与时间步t的关系曲线如图5所示，为使结果具有一般性，数据均由100次仿真结果取平均值所得.由数据可见，三种情形下平均速度随时间步的变化曲线整体趋势是一致的，但情形（1）中每一时间步平均速度基本都明显大于（2）（3）两种情形；情形（1）中，曲线经过谷底后平稳回升段的斜率要大于情形（2）（3），这是因为情形（1）中对向行人流交织后的分层现象会比情形（2）（3）中形成得更快也更明显.

分层现象的产生是行人期望顺畅移动环境的宏观体现.结伴行人在期望高步速和顺畅的移动环境的同时，也期望与结伴同伴之间保持空间上的维系，而当干扰出现时，为了实现后者期望，结伴行人往往在前者期望上作出让步，从而出现处于结伴状态的行人在空间位置和移动速度上彼此协调，使得平均速度低于个体过街行人、并阻碍分层现象产生的情况.

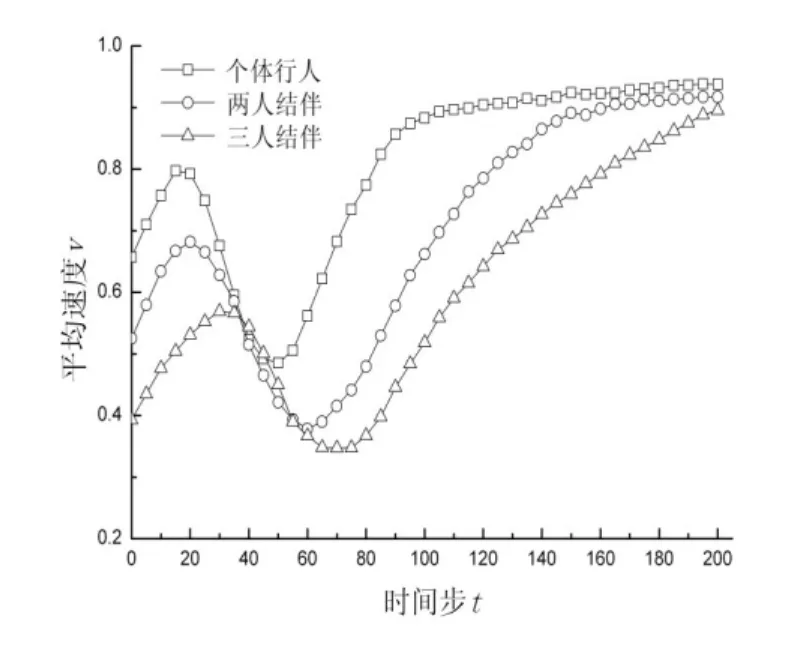
图5 N=90时不同过街行人组成情况下平均速度v与时间步t关系曲线Fig.5 The average velocity v against the time steps t according to different pedestrian formations when N=90

3.3 结伴行为对整体过街效率影响

图6为N取不同数时，系统整体的过街时间Tc与行人总数2N之间的关系变化曲线，Tc定义为从第一个行人离开等候区而进入人行横道到最后一个行人离开人行横道进入对面等候区的这段时间，数据均由100次仿真结果取平均值所得.为研究结伴行人对整体过街效率的影响，图6（a）分为三种情形：（1）n1=1，n2=0；（2）n1=0.5，n2=0.5；（3）n1=0，n2=1.即过街行人仅由个体行人和两人结伴行人组成，并逐渐增大两人结伴行人数在过街行人总数中的比例.由结果可见情形（1）的整体过街时间总是低于情形（2），而情形（2）又低于情形（3），即当过街总人数一定时，结伴行人所占的比例越大，则整体过街时间越长.说明结伴行人会降低整体过街效率，且结伴行人所占比例越大整体过街效率越低.

为研究结伴群结构对整体过街效率的影响，图 6（b）分三种情形：（1）n1=0.2，n2=0.8，n3=0；（2）n1=0.2，n2=0.4，n3=0.4；（3）n1=0.2，n2=0，n3=0.8.即保持个体行人比例不变的情况下，逐渐增大三人结伴行人数在结伴行人总数中的比例.由图中可以看出情形（1）的整体过街时间低于情形（2），而情形（2）又低于情形（3），即三人结伴行人数占结伴行人总数比例越大，整体过街时间越长.说明结伴群结构越大对整体过街效率的降低作用越大.

同时，从图6中可以看出，当行人总数2N小于50左右时，不同情形Tc之间的差距较小，而当2N大于50时，这种差距开始逐渐扩大，说明在低密度时，结伴行为对行人流整体的影响效果较小，在行人密度较大时，结伴行为对行人流整体的影响效果才会更明显.

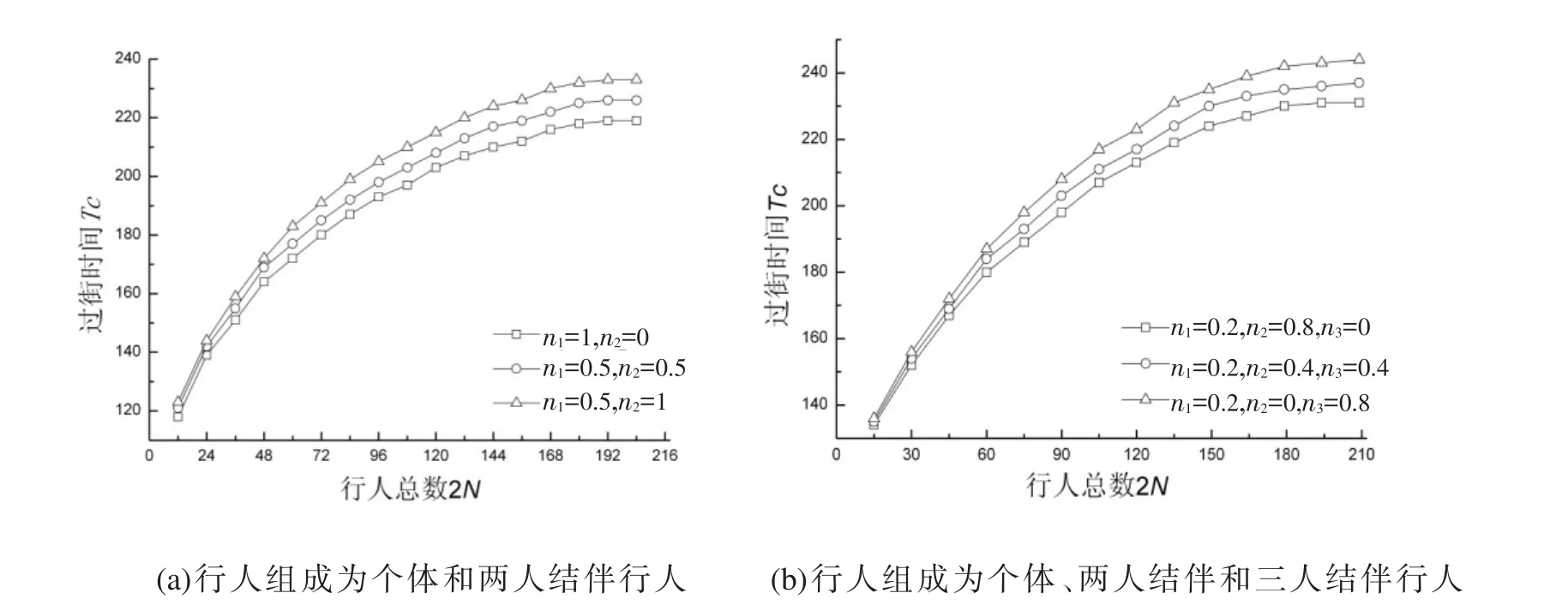
图6 不同过街行人组成情况下整体过街时间Tc与行人总数2N关系曲线Fig.6 The total crossing time Tcagainst the total number of pedestrians 2N according to different pedestrian formations

4 研究结论

本文利用元胞自动机建立了考虑结伴行为的行人过街模型，并通过控制过街行人总数及过街行人组成情况进行仿真分析.研究结果表明：由于各结伴成员之间存在彼此协调、相互影响的关系，结伴过街行人受到外界的干扰作用要大于个体行人，结伴行人平均速度一般低于个体行人，同时结伴行人会阻碍分层现象的发生；结伴行人会降低整体过街效率，结伴行人所占比例越大整体过街效率越低、结伴群结构越大对整体过街效率的降低作用也就越大.文中给出了不同过街行人总数、不同结伴行人比例和结伴群结构下结伴行人对整体过街时间Tc的影响关系.但本文只考虑了两人结伴和三人结伴的情形，研究只针对一种人行横道尺寸，对更多结伴群结构在不同尺寸人行横道下的影响关系还需要进一步的深入研究.

[1]Burstedde C,Klauck K,Schadschneider A,et al.Simula⁃tion of pedestrian dynamics using a two-dimensional cellular automaton[J].Physica A:Statistical Mechanics and its Applications,2001,295(3):507-525.

[2]Blue V J,Adler J L.Cellular automata microsimulation for modeling bi-directional pedestrian walkways[J].Transportation Research Part B:Methodological,2001,35(3):293-312.

[3]岳昊.基于元胞自动机的行人流仿真模型研究[D].北京:北京交通大学,2009.[YUE H.Study on the simula⁃tion model of pedestrian flow based on cellular automata[D].Beijing:Beijing Jiaotong University,2009.]

[4]Yue H,Hao H,Chen X,et al.Simulation of pedestrian flow on square lattice based on cellular automata model[J].Physica A:Statistical Mechanics and its Applica⁃tions,2007,384(2):567-588.

[5]LI Xiang,DONG Li-Yun.Modeling and simulation of pedestrian counter flow on a crosswalk[J].Chinese Phys⁃ics Letters,2012,29(9):98902.

[6]丁宁.路段行人过街元胞自动机仿真研究[D].哈尔滨:哈尔滨工业大学,2011.[DING N.Study on simulation of pedestrian crossing street by cellular automata at sec⁃tions[D].Harbin:Harbin Institute of Technology,2011.]

[7]Guo N,Ding J,Ling X,et al.Walking behavior of pedes⁃trian groups in the merchandise streets[C]//The Twelfth COTA International Conference of Transportation Profes⁃sionals,Beijing,China,2012.

[8]景超.行人过街交通特性研究[D].长春:吉林大学,2007.[JING C.Study on pedestrian crossing characteris⁃tics[D].Changchun:Jilin University,2007.]

[9]Zhou R,Horrey W J,Yu R.The effect of conformity ten⁃dency on pedestrians’road-crossing intentions in Chi⁃na:An application of the theory of planned behavior[J].Accident Analysis&Prevention,2009,41(3):491-497.