基于K-means聚类算法的公交运营时段分析

沈吟东，张仝辉，徐 甲

（华中科技大学 自动化学院，图像信息处理与智能控制教育部重点实验室,武汉 430074）

1 引言

近年来，我国的城市交通面临着日益严峻的挑战.公交作为城市交通一个重要的组成部分，也是城市居民正常出行最重要的交通工具之一.分析并研究公交运营情况，对公交规划、时刻表的制定及改善公交服务质量有十分重要的作用[1，2].

公交线路在不同时段的运营时间和客流规律通常存在很大差异，所以一般需要对高低平峰等不同时段分别进行分析.因此，运营时段划分是公交运营分析的重要基础.运营时段的划分研究始于上世纪80年代，Salicrú等[3]对其做了归纳总结.Carey[4]做了单程运营时间的随机性研究，将其归并到总运营成本中.国内对时段划分的研究较少，杨新苗等[5]用fisher聚类做了运营时段划分,徐甲和沈吟东[6]基于车辆定位数据采用贪心策略划分运营时段.而在现实中，公交公司基本都是根据客流和线路运营环境采用手工方式凭经验划分时段[7].然而，完全根据经验人工划分的时段一般比较粗略，与现实的运营规律之间很可能存在偏差.随着GPS定位系统的普及应用，公交企业已积累了大量的运营数据.人们逐渐认识到这些数据能够更为实时准确地反映运营状况，因此，如何合理利用大规模的数据进行运营分析成为研究的热点和难点[8].

本文拟基于GPS运营数据，利用K-means算法具有解决大规模数据聚类问题的能力，设计基于K-means聚类算法的公交运营时段划分方法，以期实现自动、准确地划分公交运营时段，为进一步的分时段运营分析和优化调度奠定基础.

2 公交运营时段分析算法

现实中，公交线路在不同时段的运营状况、拥堵情况和客流量等往往存在较大差异，致使一天内的车辆单程（从起点到终点）的运营时间变化很大[6].图1给出了从GPS记录中抽取出的一条线路一天的单程时间样本.

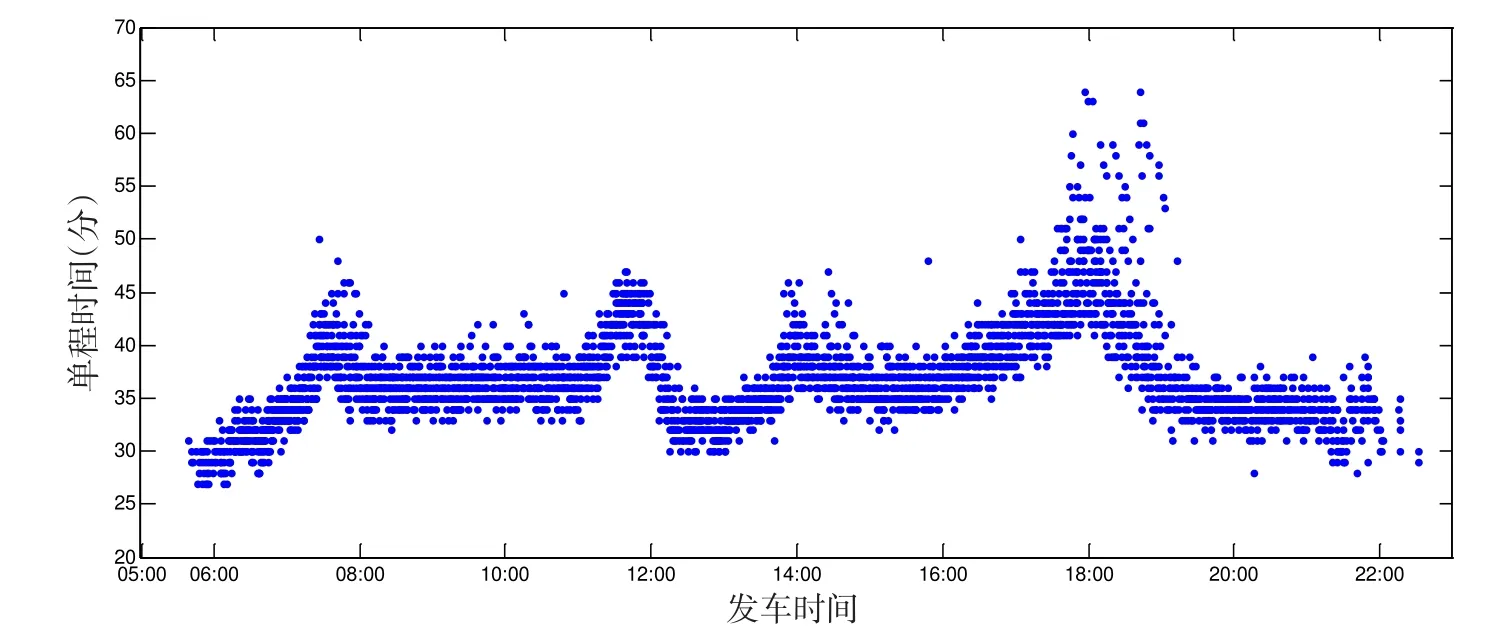
图1 一天的单程时间示意图Fig.1 Illustration of trip times during a day

从图1可见，一天的单程运营时间在不同时段存在明显差异.我国公交企业在制定运营计划时普遍将一条线路的单程时间设置为一个固定值，这显然与现实情况不太吻合，因此，编制的运营计划通常也很难按时执行，运营混乱现象难以消除.

为了编制出能够符合实际运营规律、具有高执行率的运营方案，本文采用定量的方法对公交线路全天的运营时间进行聚类分段.其中，K-means聚类算法是解决聚类问题的一种经典算法，具有效率高和易实现的特点，被广泛应用于地球科学、信息技术、决策科学、医学和商业智能等领域的对大规模数据聚类[9].因此，本文拟设计出能够有效划分运营时段的K-means聚类算法.

2.1 基于K-means聚类的运营时段划分方法

K-means聚类算法的基本思路是：设有k个簇，依据一定的测度标准，将一组给定的对象逐个赋予或重新赋予最类似的簇，该过程不断迭代直至满足预设的终止条件.下面定义K-means聚类算法的主要元素.

假设已知一个单程时间样本集合，定义其为对象集合P，其中每一个单程时间就是一个对象p∈P.任意一个簇Ci⊂P(i=1,2,...,k)表示一组相似对象的集合，即，k表示簇的总数.在公交运营时段划分问题中，可以设定k=4.因为公交线路的高低峰时段一般都可以分为如下四类：低峰、平峰、小高峰和高峰，因此单程时间样本集合中的每个对象都可以分别归入其中一类（簇）.每个簇的聚类中心称为簇中心mi(i=1,2,...,k)，定义为簇中对象的平均值，即该簇中全部单程时间的平均值.

为了使k个簇各自尽可能紧凑独立，本文使用欧几里得距离dp,mi= ||p-mi表示对象p到簇中心mi的距离，并采用平方误差准则[9],把标准测度E定义为全部对象的误差平方总和，其公式为

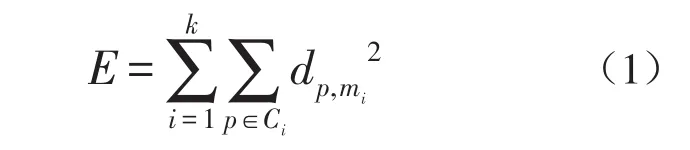
基于上述定义，本文设计出基于K-means聚类算法的运营时段划分方法，具体流程如下.

步骤1 从对象集合P中任意选择k个对象作为每个簇的初始簇中心;

步骤2 对每个对象 p∈P，计算其与各个簇中心的距离dp,mi，并将 p赋予最类似（对应dp,mi最小）的簇；

步骤3 更新簇中心 mi(i=1,2,...,k).

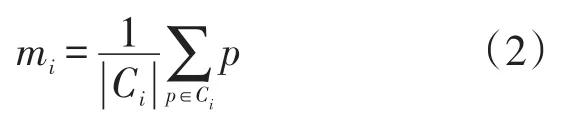
步骤4 根据式（1）计算标准测度E，如果相邻两次迭代的E的差值的绝对值小于给定限定值，则算法终止，否则，重复步骤2.

明朝继承元朝的东北疆域后，于明成祖永乐七年(1409)置奴儿干都指挥使司(简称奴儿干都司)，统辖包括今库页岛、北海道在内的黑龙江流域。

在大量的公交单程时间样本数据中通常存在着一些脏数据或异常数据（本文统称异常数据）[10]，例如因GPS设备故障或信号不好造成部分记录丢失，从而形成了一些超长单程时间记录；因GPS定位误差或匹配误差造成异常的单程时间记录；因车辆故障或交通事故等造成的异常单程时间.上述设计的K-means时段划分算法无法区别这些异常数据，因而，需要在数据预处理时，将这些数据事先加以剔除，否则，容易造成时段划分的偏差.

另外，在高低峰之间一般存在一些过渡时间段，期间，单程时间会逐渐变长或变短.由于该算法属于硬聚类算法，对于介于高低峰之间的中间值可能会造成较大的聚类误差.

为了有效处理异常数据和过渡时间段的聚类问题，以及减少不必要的距离运算，下面，我们设计了一个改进的K-means时段划分方法.

2.2 改进的K-means算法

对K-means算法的改进主要包括以下三个方面：初始簇中心的选择，优化距离计算和簇中心的更新.

(1)改进的初始簇中心选择方法.

随机选择k个初始簇中心，可能会造成簇中心过于集中或者不能均匀地分散在整个数据空间，从而导致收敛所需的迭代次数增多，甚至陷入局部最优解，影响聚类结果的准确性.为了尽量避免上述问题，下面设计了一个改进的初始簇中心选择方法，使得初始簇中心之间能够保持一定的间距、分布更为均匀.具体步骤如下：

首先，从单程时间集合P中随机选择一个初始簇中心，作为第一个簇中心m1.然后，按式(3),根据已确定的 j-1(2≤j≤k)个簇中心,逐个选择第 j个簇中心mj,直到选择出k个簇中心.

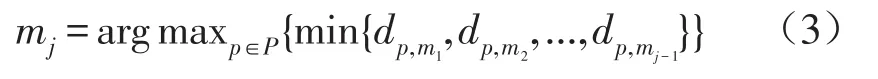
式中 dp,mj——对象 p到簇中心mj(j=1,2,...,k)的距离.

在步骤2中，需要计算每个对象p与各个簇中心的距离.然而ELKAN等人研究分析后发现很多距离的计算都是不必要的，因而提出了基于三角形不等式原理来避免冗余的距离计算[11]，其中三角形不等式定理即两边之差小于第三边和三角形两边之和大于第三边.用其来避免基础K-means算法中冗余距离计算的两个定理如下[11].

定 理1 ∀mi,mj(1≤i,j≤k),∀p∈P ，如 果2dp,mi≤dmi,mj，那么dp,mi≤dp,mj.其中，dmi,mj表示簇中心mi到mj之间的距离.

定 理2 对 ∀mi,mj(1≤i,j≤k) ，都 有dp,mj≥max{0,dp,mi-dmi,mj}成立.

由定理1可知，如果对象 p 满足2dp,mi≤dmimj，根据定理1可以判定dp,mi≤dp,mj，因此没有必要继续计算 dp,mj.特别地，如果 2dp,mi≤mini≠jdmi,mj，根据定理1可以判定mi是对象p距离最近的中心，因而没必要计算对象p和其它聚类中心的距离，这样避免了多余的距离计算.

由定理2可知，如果dp,mj的下界max{0,dp,mi-dmi,mj}大于dp,mi，则没有必要计算dp,mj，这样也可以避免多余的距离计算，达到优化计算的目的.

(3)改进的簇中心更新算法.

基本的K-means算法属于硬聚类算法，对介于高低峰之间的中间值可能会造成较大的聚类误差[12].为了减少硬聚类的误差，本文改进了簇中心mi的更新策略,即对于介于两个簇Ci和Cj之间的任意对象p，用式(4)替代式(2)更新簇中心mi.

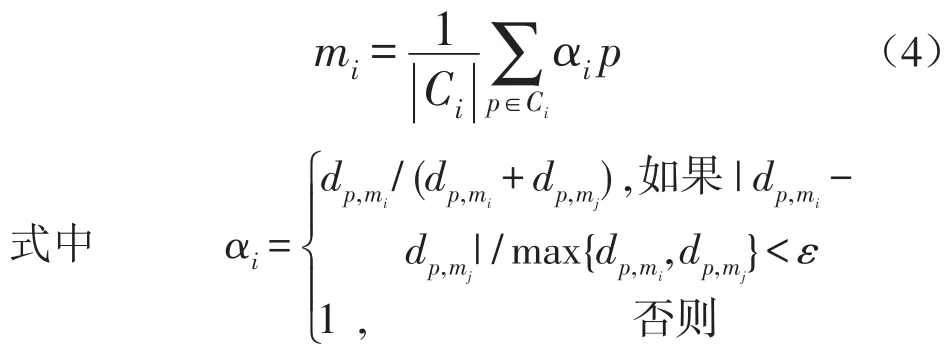
式(4)中采用了一个模糊因子αi(0≤αi≤1)，表示对象p对簇中心的影响程度，αi越大则影响越大.ε为临界值参数，当|dp,mi-dp,mj|/max{dp,mi,dp,mj}小于该临界值时，对象p对簇中心的影响被减弱.

3 案例分析

3.1 湖北十堰4路案例分析

本中通过对十堰市公交4路2011年10月一整月的数据的分析，在对23437条单程数据按天分上下行统计处理过程中发现，国庆期间、平日和周末的单程时间的区段分布特点有比较大的不同，故分别加以分析.由于平日、周末和国庆的分析方法大体相同，所以案例分析中只以平日分析为例.此外，为了避免异常数据对时段划分准确性的影响，必须事先将各种异常数据加以剔除.通过设置样本数据的上下限阈值，即限定正常情况下样本可能出现的最大、最小值.从而使得在聚类过程中自动剔除异常数据，从而增强算法的适应性、降低异常数据对算法的影响.对该线路的数据研究分析后，正常的单程样本的下限为20分，上限为70分.因而异常数据的自动过滤中所取的下限为20分，上限为70分.数据预处理后平日上下行的单程时间样本数据分别如图2和图3所示.图2和图3分别给出了平日上下行的单程时间样本数据的散点图.

根据公交线路特点,设定簇的个数k=4，分别对应低峰、平峰、小高峰和高峰时段.临界值选取了四种情形，即ε∈{0,0.25,0.5,1}分别进行运营时段划分，结果详见表1.

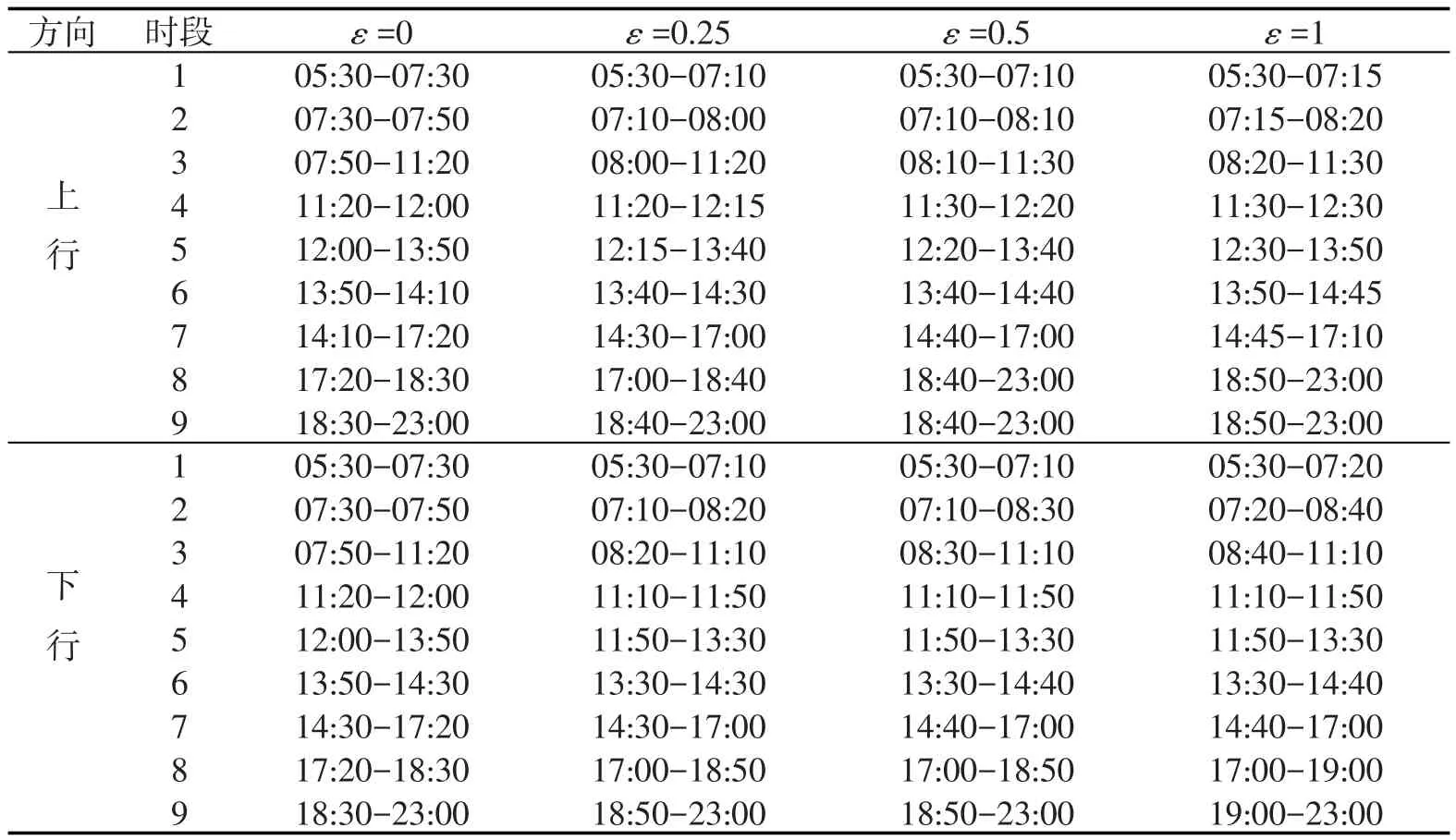
表1 利用改进的K-means算法依据不同ε值的运营时段划分Table 1 The time periods generated by the improved K-means algorithm with differentε

从表1可见，由于高低峰过渡时段中居中的部分（即高峰时段的1/4部分）单程时间变化率较大，因而临界值选取ε=0.25与现实规律更为符合.为了验证上述时段分析结果的合理性，下面阐述实际调研结果，以验证聚类算法划分运营区段的合理性.十堰4路实际的公交运营状况是第一个高峰出现在早上7:00到8:30之间，这个时候的单程时间增加迅速，从开始的30分增加到45分左右，有的甚至达到了1个小时.这个时间段单程时间出现高峰的原因主要是，此时处于早高峰时期，客流主要是上班上学人群，不管是乘坐公交还是驾私家车的人群都达到了一天中最多的时候，加上路面的交通状况拥堵，公交运营中很容易产生大间隔，造成单程时间大幅度增加.由此可见，改进的K-means算法与现实中的规律较为吻合，验证了其理论的正确性.而传统的K-means算法则划分的早高峰时间段较小，与现实不太吻合.同理，其它的高峰时间段K-means算法所划分的时间段均出现了高峰时间段划分区间较小的现象，而改进算法则很好地克服了这个问题，其时间段的划分及各时段内的单程均值与上述介绍的十堰4路公交实际情况基本吻合.

本文利用K-means聚类算法和改进的K-means聚类算法分别进行了时段划分，结果如图2和图3所示，其中，虚线和黑细线分别代表K-means和改进的K-means聚类算法(ε=0.25)所计算出的时段划分结果，黑粗线代表两种方法的分割线重合.

从图2和图3中我们可以看出，单程时间的全天分布都呈现出四个波峰段，早高峰、两个午高峰、晚高峰.其中，在上行的晚高峰时段单程时间明显最长，高峰时段也持续最长.

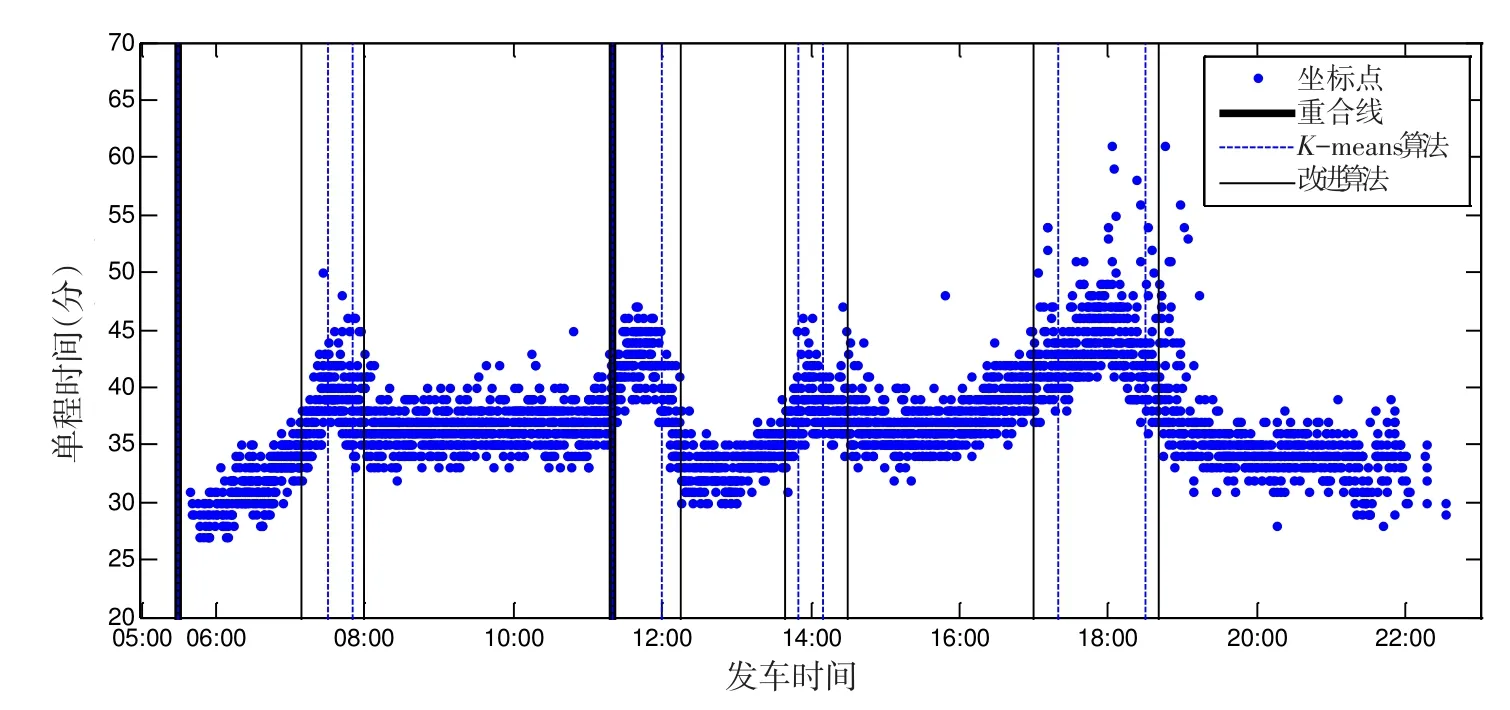
图2 十堰4路单程时间样本及两种K-means聚类算法的时段划分结果（平日上行）Fig.2 Trip times and time periods produced by two K-means algorithms(Weekday,outbound)

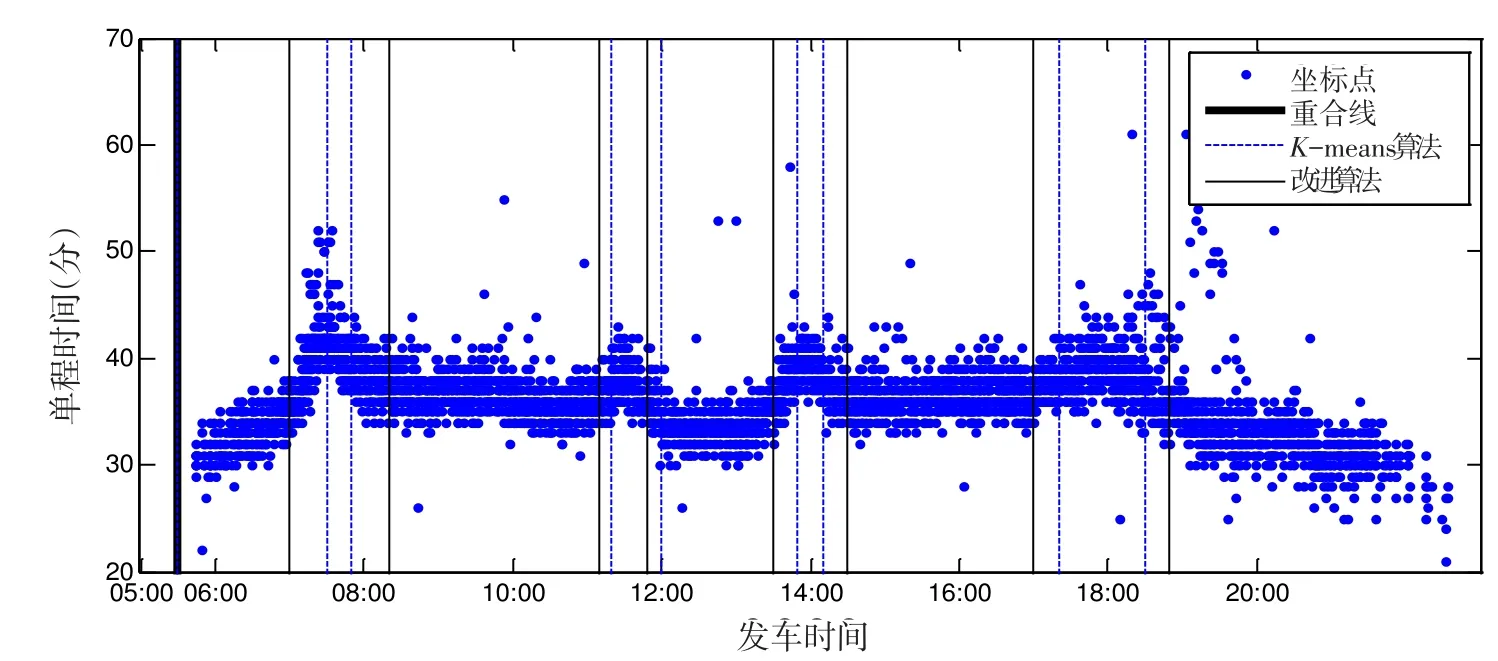
图3 十堰4路单程时间样本及两种K-means聚类算法的时段划分结果（平日下行）Fig.3 Trip times and time periods produced by two K-means algorithms(Weekday,inbound)

3.2 海南海口4路案例分析

本中通过对海口市公交4路2010年7月平日上行4237条单程数据的研究分析，设置样本数据的上下限阈值，即异常数据的自动过滤中所取的下限为30分，上限为80分.数据预处理后平日上行的单程时间样本数据分别如图4所示.对临界值ε∈{0,0.25,0.5,1}这四种情形分别划分出的运营时段如表2所示.

由于高低峰过渡时段中居中的部分(即高峰时段的1/4部分)单程时间变化率较大，因而临界值选取ε=0.25与现实规律更为符合.本文利用K-means聚类算法和改进的K-means聚类算法分别进行了时段划分，结果如图4所示.其中，虚线和黑细线分别代表K-means和改进的K-means聚类算法(ε=0.25)所计算出的时段划分结果，黑粗线代表两种方法的分割线重合了.文中K-means聚类算法和改进的K-means聚类算法所得出的结果与实际公交规律均较为符合，改进的K-means聚类算法更贴合实际一些.

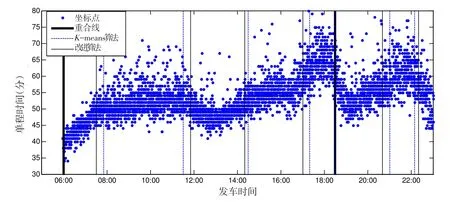
图4 海口4路单程时间样本及两种K-means聚类算法的时段划分结果（平日上行）Fig.4 Trip times and time periods produced by two K-means algorithms(Weekday,outbound)

4 研究结论

本文围绕公交运营时段划分展开了深入研究，创新性地提出基于聚类方式的公交运营时段划分方法.利用聚类方法能够更为客观准确地划分运营时段，克服了手工划分方法主观性和精度不高的缺点.通过对公交GPS运营记录数据的挖掘，提出了一个基于K-means聚类方法的公交运营时段划分方法，并进一步从初始簇中心点的选择、异常数据的自动过滤、基于三角形不等式和模糊聚类的簇中心的更新等三个方面改进了该K-means聚类时段划分方法.

通过对十堰市4路和海口市4路的实际公交运营数据进行案例分析，基本的K-means算法和改进的K-means算法都能够基于单程时间样本求解出运营时段的划分结果.实验结果表明：两种算法得到的时段划分与现实规律都基本吻合.但是，基本的K-means算法划分的高峰时间段有些偏窄，而改进的K-means算法所划分的时间段及其单程均值与现实规律更加吻合.在编制车辆运营计划时，必须确定时刻表中所有单程任务的时间，目前国内企业操作时均采用人工经验法.文中案例分析部分中的十堰4路和海口4路就是基于人工经验的方法，而在实际运营中的单程时间是受道路交通条件、客流等多方面因素影响的，变化规律复杂，凭借人工经验难以精确把握，必须基于大量的真实数据，采用科学的统计工具来分析，这种工作量是人工难以负担的.从该角度上来说，本方法的优点就是可以从大量的现实的运营纪录中，准确分析单程时间的变化规律，划分时间段，并求出每个时间段中的平均单程时间，这为进一步的分时段进行运营分析，以及编制高准点率的运营调度方案奠定了重要基础.

[1]Ceder A.Public-transport vehicle scheduling with multi vehicle-type[J].Journal of Transportation Research,2011,19(3),485-497.

[2]Hickman M,Mirchandani P,Voß S(Eds).Computer-aid⁃ed systems in public transport[C]//Lecture Notes in Eco⁃nomics and Mathematical Systems,Volume 600.Berlin:Springer,2008.

[3]Salicrú M,Fleurent C,Armengol J M.Timetable-based operation in urban transport:Run-time optimisation and improvements in the operating process[J].Transporta⁃tion Research Part A,2011,45(8):721-740.

[4]Carey M.Reliability of interconnected scheduled servic⁃es[J].European Journal of Operational Research,1994,79(1):51-72.

[5]杨新苗，王炜，尹红亮，等.基于公交调度峰值曲线的优化方法[J].东南大学学报，2001，31(3):31-35.[YANGX M,WANG W,YIN H L,et al.A new method for transit peak value curve optimization[J].Journal of Southeast University,2011,31(3):31-35.]

[6]徐甲，沈吟东.基于AVL数据的单程时间参数设置方法[J].交通运输系统工程与信息，2012,12(5):39-45.[XU J,SHEN Y D.Setting scheduled trip time based on AVL data[J].Jo urnal of Transportation Systems Engi⁃neering and Information Technology 2012,12(5):39-45.]

[7]张景，沈吟东.基于定位数据的公交时间站点自动选择方法[J].交通运输系统工程与信息，2012,12(6):60-65.[ZHANG J,SHEN Y D.Auto⁃matic selection of time points based on AVL data[J].Journal of Transportation Systems Engineering and Infor⁃mation Technology 2012,12(6):60-65.]

[8]Shen Y,Xia J.Integrated bus transit scheduling for the Beijing bus group based on a unified mode of operation[J].International Transactions in Operational Research,2009,16(2):227-242.

[9]黄震华，向阳，张波.一种进行K-Means聚类的有效方法[J].模式识别与人工智能，2010,23(4):516-521.[HUANG Z H,XIANG Y,ZHANG B.An effecient meth⁃od for K-means clustering[J].Pattem Recognition and Aitificial Intelligence,2010,23(4):516-521.]

[10]Ceder A.Optimal multi-vehicle type transit timetabling and vehicle scheduling[J].Procedia Social and Behavior⁃al Sciences,2011,20(0)：19-30.

[11]Elkan C.Using the trangle inequality to accelerate K-means[C]//Proceedings of Twentieth International Con⁃ference on Machine Learning.Washington,DC,USA,2003:1-7.

[12] 刘健，张宁.基于模糊聚类的城际高铁乘客出行行为实证研究[J].交通运输系统工程与信息，2012,12(6):100-105.[LIU J,ZHANG N.Empirical research of inter⁃city high-speed rail passengers’travel behavior based on fuzzy clustering model[J].2012,12(6):100-105.]