基于切换系统的过饱和信号交叉口混杂控制
向伟铭,肖 建,蒋阳升
(西南交通大学 交通运输与物流学院,成都610031)
1 引言
信号交叉口的控制一直都是城市交通控制的核心问题之一,经多年发展已形成了一系列研究成果[1-3],关于过饱和信号交叉口的控制和优化是当前研究的重点和热点.目前过饱和交叉口信号灯的设置主要分为离线与在线两种方式,但已有成果大多忽视了信号周期内各相位之间的切换行为.事实上,信号交叉口是一个典型的混杂系统,同时包含了排队车辆的连续动态行为与信号灯相位的逻辑控制.近年来,越来越多的研究者利用混杂系统理论来对信号交叉口进行分析和研究[4-7].从某种意义上来说,交叉口排队车辆的消散问题可以看作交叉口系统稳定性问题[4,5];而排队溢出问题则可看作系统的有界性问题.因此有必要从系统稳定性与有界性的角度来对信号交叉口进行分析和设计.Lyapunov函数方法一直以来都是解决系统稳定性与有界性的有效工具[8],但目前基于Lyapunov方法来设计交叉口信号控制策略的成果却还不多见,尤其是同时研究排队车辆数稳定与有界性的结论很少.因此,本文在考虑信号交叉口为混杂系统的同时,将Lyapunov方法引入到过饱和交叉口的控制中.
切换系统是混杂动态系统一种常见的模型[9].本文首先将信号交叉口建模为离散时间切换系统,基于Lyapunov方法设计了状态反馈控制器来设置每个相位的有效绿灯时间,保证了信号交叉口指数稳定,使得排队车辆迅速消散.而后通过考虑系统的有界性,尽量降低消散过程中的最大排队车辆数来避免排队溢出.最后设计了混杂控制策略来动态地设置绿灯时间.与韦伯斯特方法比较,本文的混杂控制策略能够达到更好的排队车辆消散效果.
2 问题描述与建模
2.1 离散时间切换系统模型
离散时间切换系统的数学模型如下:

式中 x(k)∈Rn为状态;u(k)∈Rm为控制输入;σ(k):Z+→ℐ为切换规则;其中ℐ:={1,2,…,N}为子系统标示集合.若考虑子系统为线性时不变系统,式(1)表示如下:
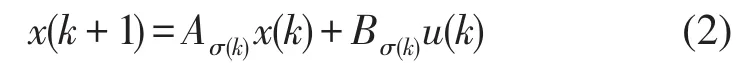
若对线性切换系统(2)设计状态反馈控制器u(k)=Kσ(k)x(k),则得到闭环系统

指数稳定性与有限时间稳定性的定义如下:
定义1[8]考虑系统(1),当u(k)=0,若∃λ>0,对 ∀ε>0 ,∃δ=δ(ε)>0 ,使 得 初 始 状 态 满 足x(k0)≤δ时,满足 ‖x(k)-x*‖≤εe-λ(k-k0),∀k≥k0,则平衡点x*是指数稳定的.
定义2[10]考虑系统(1),其中 u(k)=0.给定(δ,ε,R,T),其中0≤ δ<ε,T>0,矩阵R>0 ,若 x(k)满 足,其中.则称系统(1)是关于(δ,ε,R,T)有限时间稳定的.
2.2 单交叉口的离散时间切换模型的建立
本文考虑单交叉口具有4个相位,8个车道,如图1所示.
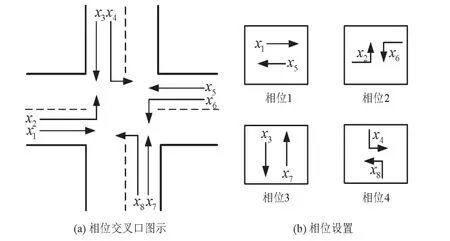
图1 相位交叉口图示及相位设置Fig.1 Illustration of intersection and phase setting
假设交通灯只有红绿两种状态,按相位1→相位2→相位3→相位4进行切换,每个切换时刻为时刻k,k≥k0.定义如下变量:
k时刻开始工作的相位i的绿灯时间:gi(k),i∈{1,2,3,4}
l车道的车辆到达率:ql,l∈{1,2,…,8}
l车道的饱和流量:sl,l∈{1,2,…,8}
l车道在k时刻的排队车辆数:xl(k),l∈{1,2,…,8}
以相位1为例,有
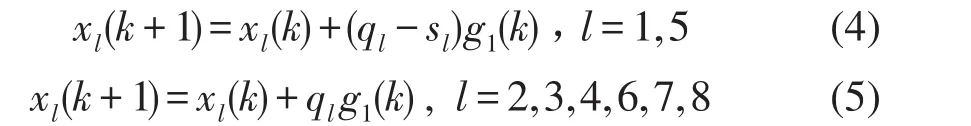
其他相位2、3、4类似,因此系统可写成以下紧凑形式:

式中 x(k)=[x1(k)x2(k)…x8(k)]T,u(k)=gσ(k)(k),矩阵Ai=I,∀i=1,2,3,4,以 及 B1=[q1-s1q2q3q4q5-s5q6q7q8]T,B2=[q1q2-s2q3q4q5q6-s6q7q8]T,B3=[q1q2q3-s3q4q5q6q7-s7q8]T,B4=[q1q2q3q4-s4q5q6q7q8-s8]T.系统的切换规则为

当车道数较多时,可考虑几个车道的排队车辆总数来达到降维的目的.例如考虑图1,令东西方向车道上车辆数之和y1=x1+x2+x5+x6,以及南北方向车道上车辆数之和y2=x3+x4+x7+x8,则可得降维模型:
式中 输入和切换规则与系统(6)相同,状态y(k)=[y1(k)y2(k)]T,矩阵 Ai=I,∀i=1,2,3,4,以及可以看到系统维数由8降低到了2.
交叉口的过饱和控制的目的是让排队车辆迅速消散.由定义1,该问题可看作设计u(k)=Kσ(k)x(k)使得闭环系统(3)关于x*=0指数稳定.
问题1 考虑信号交叉口模型(6)或(7),设计状态反馈控制器使得闭环系统(3)指数稳定.
另一方面,排队溢出问题可看为排队车辆数的有界性问题.由定义2,该问题为尽量降低系统关于x*=0的有限时间稳定(T→∞)的边界ε问题.
问题2 考虑信号交叉口模型(6)或(7),设计状态反馈控制器使得闭环系统(3)指数稳定且有限时间稳定(T→∞)的边界ε最小.
3 信号交叉口的稳定性与有界性分析
3.1 稳定性分析
首先,定义集合 ℐi,j∈ℐi表示相位i后的工作相位j.然后,给出常用的Schur补引理:
引理1[11]给定矩阵有Q<0
最后,因为本文控制方法需要实时获得交叉口的排队车辆数,因此满足以下假设:
假设1 假设每条道路的排队车辆数在每个相位切换时刻是能够在线测量的.
在满足假设1的情况下,可以得到以下结论:
定理1 考虑系统(6),若存在正定矩阵Qi,i∈ℐ及0<μ<1,使得∀j∈ℐi,∀i∈ℐ ,有
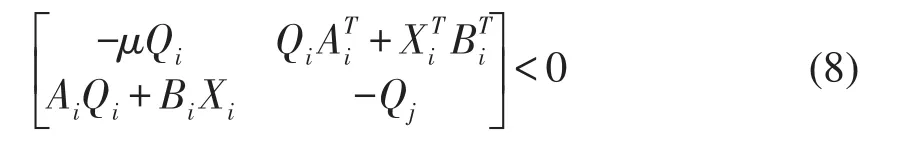
则在 u(k)=Kσ(k)x(k),其中的控制下,闭环系统是指数稳定的.
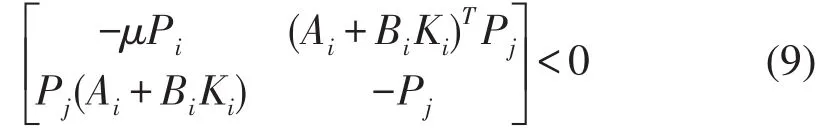
再由引理1得到

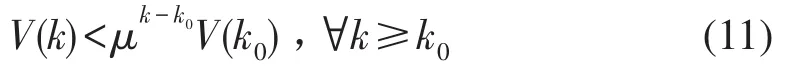
另外因为Qi正定,为正定矩阵.易证存在 λmax≥λmin>0满足 λminI≤Pi≤λmaxI,∀i∈ℐ.因此有εe-λ(k-k0),其中[λ=-(lnμ)/2>0].由定义1可知闭环系统是指数稳定的.
注1 定理1的条件可以方便地利用MATLAB中的LMI(线性矩阵不等式)工具箱求解[11].定理1表明绿灯时间设置为u(k)=Kσ(k)x(k)就可保证排队车辆能够指数消散.特别地,参数0<μ<1还表示了排队车辆数指数递减律的估计.
3.2 有界性分析
首先,任意正定对称矩阵R∈Rn×n均可分解为R=(R12)TR12,其中 R12∈Rn×n也是对称正定矩阵.另外,R的逆矩阵R-1∈Rn×n必定存在.使得
定理2 考虑系统(6),若存在正定矩阵Qi,i∈ℐ 及 0<μ<1,γ>1,使得式(8)成立以及∀i∈ℐ,有
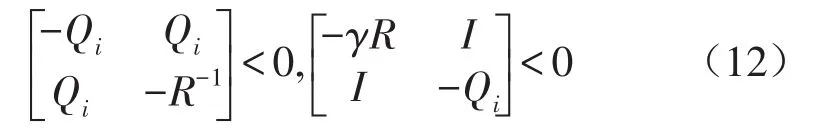

证明 当式(8)成立时,由定理1可得系统是指数稳定的,并且有
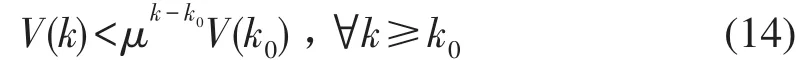
由式(14)可得排队车辆数xT(k)Rx(k)的边界ε,可估计为.给定初始排队车辆数的情况下,为了避免排队车辆溢出,应使γ尽量小.于是可以构造以下凸优化问题:

获得最优Ki,i∈ℐ及最小边界
4 过饱和信号交叉口的混杂控制策略
考虑绿灯时间 gi(k)∈[gmin,gmax],∀i∈ℐ,另外在未饱和时仍采用常用的控制策略,使用韦伯斯特方法设置绿灯时间不失一般性因此考虑混杂控制策略:
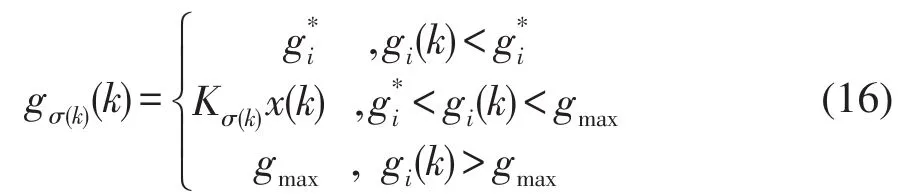
考虑图1,假设 q1=q3=q5=q7=0.35 veh/s,q2=q4=q6=q8=0.3 veh/s;s1=s3=s5=s7=1.5 veh/s,s2=s4=s6=s8=1.3 veh/s;gmin=15 s,gmax=120 s.首先通过韦伯斯特方法得;初始值xT(0)=[50 50…50].由于模型(6)的维数太高找不到可行解,考虑降维模型(7).通过定理2,取 μ=0.9得 K1=[0.483 2-0.137 3],K2=[0.536 5-0.232 8],K3=[-0.137 2 0.483 2],K4=[-0.232 8 0.536 5].与韦伯斯特方法相比,混杂控制策略能够动态地调整绿灯时间长短,对应有效绿灯时间如图2所示.
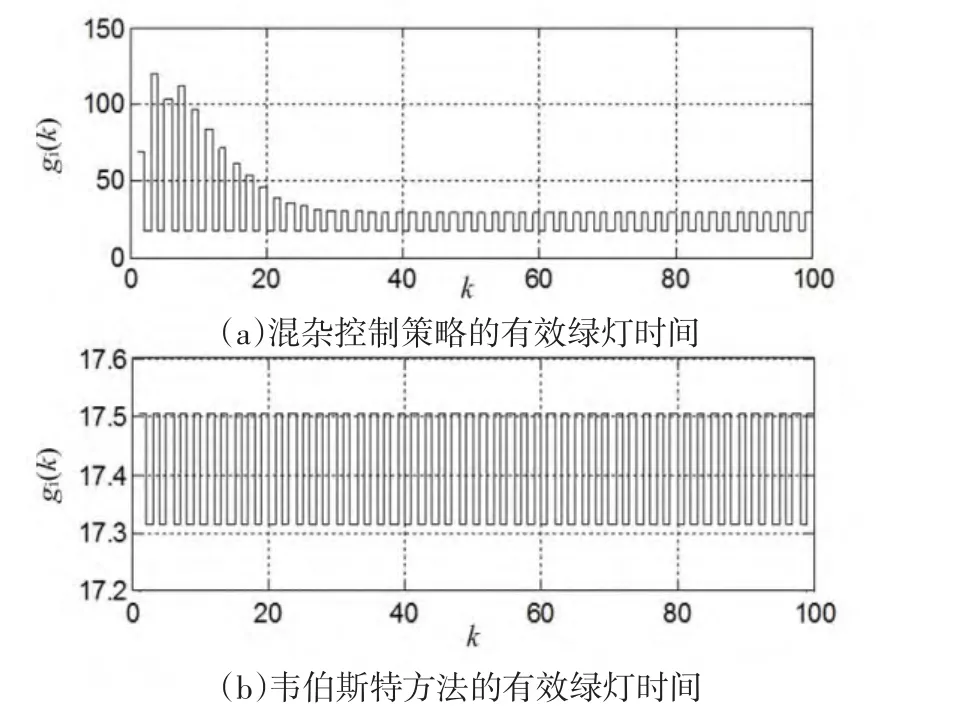
图2 两种方法下的绿灯时间设置Fig.2 Green time settings with two methods
由图2可以看到,在排队车辆较多的时候,混杂控制策略所得的绿灯时间明显与韦伯斯特方法不同,因此混杂控制策略特别适合过饱和程度较严重的交叉口的控制.最后为了清晰地比较两种方法下排队车辆消散以及估计边界,我们考察即令定理2中的 R=I,求解式(15)得 γmin=1.475 4,并计算最小边界εmin=417.302 1.图3给出了两种方法下 ‖x( k)‖递减的规律与估计边界.
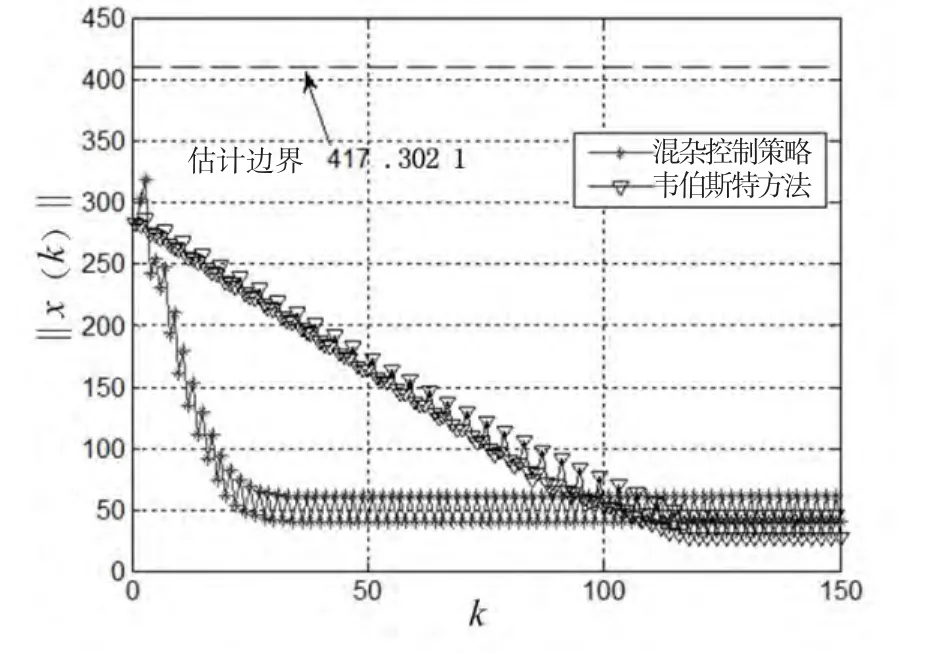
图3 排队车辆数 ‖x( k)‖的规律及估计边界Fig.3 Evolution of vehicles ‖x(k)‖and estimated boundary
混杂控制策略下车辆消散的速度更快,大约在k≈25左右就进入了未饱和状态,而韦伯斯特方法却要在k≈120之后才能进入未饱和状态.因此本文提出的混杂控制策略更加适合过饱和交叉口的控制.
5 研究结论
在交通路口中,动态的车流具有连续时间特性,而信号灯的切换具有离散事件特性,这导致传统的方法难以对这类问题进行建模和分析.本文利用离散时间切换系统来对信号交叉口进行建模,将排队车辆消散看作系统的稳定性问题.基于Lyapunov方法,分析了系统的稳定性及有界性,设计了反馈控制器来确定绿灯时间.最后提出了混杂控制策略.仿真结果表明,该方法具有很好的排队车辆消散效果.
[1]Chang T,Lin J.Optimal signal timing for an oversaturated intersection[J].Transportation Research B,2000,34(6):471–491.
[2]Schutter B.Moor B.Optimal traffic light for a single intersection[J].European Journal of Control,1998,4(3):260–276.
[3]Motawej F,Bouyekhf R,Moudni A E.A dissipativitybased approach to traffic signal control for an over-saturated intersection[J].Journal of the Franklin Institute,2011,348:703–717.
[4]陈阳舟,李宏峰,倪金.T形交叉口信号配时的周期线性微分自动机建模与分析[J].控制理论与应用,2011,28(12):1173-1178.[CHEN Y Z,LI H F,NI J.Modeling and analysis of cyclic linear differential automata for T-intersection signal timing[J].Control Theory&Applications,2011,28(12):1173-1178.]
[5]何忠贺,陈阳舟,石建军.切换服务系统的稳定性及交叉口信号配时[J].控制理论与应用,2013,30(2):194-200.[HE Z H,CHEN Y Z,SHI J J.Stability of switched server system and signal timing of intersection[J].Control Theory&Applications,2013,30(2):194-200.]
[6]江光秀,陈阳舟,张利国,等.基于矩形混杂自动机的交叉口建模及可达性分析[J].交通运输系统工程与信息,2009,9(4):120-126.[JIANG G X,CHEN Y Z,ZHANG L G,et al.Modeling and reachability analysis for single intersection based on rectangular hybrid automata[J].Journal of Transportation Systems Engineering and Information Technology,2009,9(4):120-126.]
[7]赵晓华,陈阳舟.基于混杂系统理论的单交叉口信号灯控制[J].北京工业大学学报,2004,30(4):412-416.[ZHAO X H,CHEN Y Z.Traffic light control method for a single intersection based on hybrid systems theory[J].Journal of Beijing University of Technology,2004,30(4):412-416.]
[8]肖建,张友刚.线性系统理论[M].成都:西南交通大学出版社,2011.[XIAO J,ZHANG Y G.Theory of linear system[M].Chengdu:Southwest Jiaotong University Press,2011.]
[9]Decarlo R A,Branicky M S,Pettersson S,et al.Perspectives and results on the stability and stabilization of hybrid systems[J].Proceedings of IEEE,2000,88(7):1069-1082.
[10]Xiang W,Xiao J.H∞finite-time control for switched nonlinear discrete-time systems with norm-bounded disturbance[J].Journal of the Franklin Institute,2011,348(2):331-352.
[11]俞立.鲁棒控制:线性矩阵不等式处理方法[M].北京:清华大学出版社,2002.[YU L.Robust control:linear matrix inequality method[M].Beijing:Tsinghua University Press,2002.]

