驾驶员反应时间对行车安全的影响

吕集尔，朱留华，郑容森，韦艳芳

(玉林师范学院 电子与通信工程学院，广西 玉林537000)

1 引言

近年来，随着公路建设的快速发展，公路交通安全问题越来越受到人们的关注.最近世界卫生组织的一份交通事故调查显示，大约有50%～60%的交通事故与酒后驾车有关.我国于2012年发布的全国道路交通事故调查结果显示，1996年至2012年因酒后及疲劳驾驶造成的交通事故的概率居高不下.此外，一些女性穿高跟鞋驾车的行为，也贡献了一定的交通事故概率.酒后驾车、疲劳驾驶及不良驾驶行为，会直接导致驾驶员反应迟钝，极易酿成重大交通事故，严重威胁出行人员的生命与财产安全.

行驶于公路上的车辆之间存在着强烈相互作用，是一个涉及多自由度的复杂体系.在诸多的交通流研究模型中，元胞自动机因其独特的优越性而得到众多研究人员的青睐.基于NaSch元胞自动机交通流模型，许多学者建立起能更精细地刻画现实交通状况的改进模型，对于改善现行的交通状况，取得了丰硕的成果[1-6].此外，NaSch元胞自动机模型经过改进后，可以用于道路交通安全问题的研究.近年来，国内外的学者在这一方面做了许多开拓性的工作[7-12].本文通过研究驾驶员反应时间对行车安全的影响，试图提出一种道路交通安全的新策略.

2 模 型

将NaSch模型的第(1)步和第(2)步合并为：vi(t+2 3)=min(Vmax,vi(t)+1,di(t)).第(3)步以概率 p随机减速：vi(t+1)=min(Vmax-1,vi(t),max(0,di(t)-1))；以概率（1-p）保持不变：

因此，无论减速行为是否发生，总满足条件：

最简单的元胞自动机交通流模型是Wolfram提出的184号规则.Nagel和Schreckenberg将184号规则模型推广到了最大速度大于1及考虑随机慢化影响的更一般情形，提出了著名的NaSch模型[13].其基本思想是：将道路视为由L个格点组成的一维格点链，每个格点代表7.5 m长，每一格点或为空或被一辆速度为v的车辆占据，速度取0～Vmax间的离散值，即 v∈{0,1,2,…,Vmax}，其中Vmax为车辆允许的最大速度，所有车辆运动方向一致.模型采用周期性边界条件，设di(t)=xi+1(t)-xi(t)-1表示第i辆车与前一辆车（第i+1辆车）间的空格点数.车辆采用4步并行更新规则：

（1）加速 vi(t+1/3)=min(vi(t)+1,Vmax)；

（2）减速 vi(t+2/3)=min(vi(t+1/3),di(t))；

（3）随机慢化vi(t+1)=max(vi(t+2/3)-1,0)以概率p发生；

（4）位置更新，xi(t+1)=xi(t)+vi(t+1).

虽然NaSch模型的规则很简单，但是可以模拟出很多实际交通现象，如时走时停交通波、幽灵式堵塞等.

目前，我国高速公路上同向行驶的车辆之间几乎是完全跟车状态，即后方的跟随车辆会根据前车的运动状态，预计前车在下一时刻所能到达的位置，及时填补其留下的空隙，为此需要计入前车速度的影响.

不等号的右侧是第i辆车在下一时刻的最低速度.这一速度可作为后方车辆（第i-1辆车）驾驶员眼中的虚拟速度.这也正是上面提到的需要计入的前车速度，实现车辆之间的动态追踪.为此，引入一种改进的元胞自动机交通流模型[14].

(1)计算前车（第i+1辆车）的虚拟速度：

(2)计算目标车辆（第i辆车）的更新速度：

(3)目标车辆的随机慢化：

(4)目标车辆的位置更新：

在此模型中，可获得一个驾驶员安全行车的条件.假设前车在当前时刻是运动的，在下一时刻即将刹车.那么安全条件应该满足[15]：

式中 D为刹车间距；τvi(t)为驾驶员在反应时间τ的行车距离.

若令γ为汽车刹车时的减速度，则方程（1）变成

根据NaSch模型第（2）步，可知汽车的减速度是无界的，故.因此安全方程变成

如果有下列事件发生，那么在t+1时刻，相邻的第i和i+1辆车之间将出现安全隐患：

事件1，反应时间内的行车距离超过当前车辆与前车之间的间距；事件2，前车在t时刻是运动的；事件3，前车在t+1时刻突然静止.这三个条件可以简化成最简单的数学表达式：

汽车驾驶员从决定刹车到踩下刹车的这段时间称为反应时间，普通驾驶员正常的反应时间在0.3–1.0 s范围内.驾驶员在没有饮酒的情况下行车，发现前方有危险情况，从视觉感知到踩制动器的反应时间约为0.5 s；饮酒后尚能驾车的情况下反应时间要减慢3-5倍；醉酒驾车情况更为糟糕.

3 数值模拟与分析

模拟时采用周期性边界条件，取L=5 000 cells组成一维格点链，每个格点对应的实际道路长为7.5 m，整个格点链对应的实际道路长为37.5 km，设道路上车辆总数为N，车辆最大速度取Vmax=5 cells/s，对应的实际车速为135 km/h.其中车辆密度ρ、平均速度vˉ和平均车流量J的计算公式如下：

初始时刻所有车辆以给定的密度ρ随机分布在一维格点链L上.为消除暂态影响，每次运行对最初的5×104时步不做统计.以后1×104时步进行时间平均，这样就得到了每一次运行的结果.取样本数为30，本文数值模拟图上的每个点是30次运行的平均值.

3.1 车流状态演化

从图1可以看出，本文模型在p=0.1时的最大流量约为 J=0.78 veh/s≈2 800 veh/h，高 于 文献[16]所给出的加利福尼亚一条高速公路上的最大流量值(2 500 veh/h)；在p=0.3时的最大流量约为J=0.59 veh/s≈2 100 veh/h，低于实测的最大流量值.因此，在对实际交通进行模拟时，参数p设置为0.2比较适宜.

图1 （a）不同延迟概率下的基本图；（b）加利福尼亚一条公路上实测数据得到的平均速度与流量关系Fig.1 （a）The fundamental diagrams for different delay probabilities；（b）The relationship between average velocity and flow obtained from a real measurement of a freeway in California

图2 车辆的时空演化图（a）ρ=0.10；（b）ρ=0.25Fig.2 The evolution diagram of position and time（a）ρ=0.10；（b）ρ=0.25

为了具体地描述车道上的车流随车流密度增加而出现由畅行相向宽幅运动阻塞相的转变，本文模拟了车辆运动过程中车辆位置与运动时间的关系图.取参数 p=0.2；Vmax=5，模拟的空间位置为2 100~2 600，时间为50 000~50 400.图中黑点表示车辆，白色表示空白区域，观察图2发现：系统在低密度下表现为自由流，在高密度下表现为“时走时停”交通波.这与实际观测到的道路交通非常吻合.从而直接说明采用此模型去模拟驾驶员反应时间对行车安全的影响是切实可行的.

为了更直观地描述车道上车辆的运动方式，本文给出了车辆的运动速度随时间的演化图.取参数 p=0.2；Vmax=5，模拟的空间位置为2 100~2 150，时间为50 000~50 020.图3中黑点表示空置格点，数字表示运动车辆的速度.观察图3(a)发现：在低密度下，车辆之间有足够的安全距离，安全隐患很少出现，甚至不出现（限于图片的规格未能画出整个车道上车辆的速度演化）.从3(b)可以看出：随着车流密度的增加，行驶中的车辆出现了追尾现象，暴露了真实存在的交通安全隐患，这一结果与实际的交通情形相吻合.

图3 车辆的速度演化图（a）ρ=0.10；（b）ρ=0.25Fig.3 The evolution diagram of speed（a）ρ=0.10；（b）ρ=0.25

3.2 反应时间对行车安全的影响

3.2.1 驾驶员反应时间延迟原因分析

(1)酒后驾驶.

酒精会使驾驶员的触觉能力，判断力与操作能力降低，可能会出现视觉障碍，还会出现过激的心理异常反应，反应迟钝等.

(2)疲劳驾驶.

驾驶员疲劳后继续驾驶车辆，会出现困倦瞌睡，四肢无力，注意力不集中，判断能力下降等情况，甚至会出现精神恍惚，瞬间记忆消失等极端情形，反应时间较正常水平大为增加.

(3)不当驾驶穿着.

所谓不当驾驶穿着，是指驾驶员驾驶机动车时穿高跟鞋、拖鞋或赤脚等不良行为.这种不当驾驶行为会导致驾驶员的双脚滑落踏板的几率相对增加，严重影响踩刹车或离合器踏板的力度和角度，延长反应时间.当遇到紧急情况时无法及时实施制动措施，同速行驶下的制动距离也相应延长.

3.2.2 追尾事故的数值模拟分析

图4（a）模拟了不同反应时间对道路交通安全的影响.在中等车流密度下，车辆发生追尾事故的概率随反应时间的延长显著增加，几乎正比于反应时间.在较低或较高的车流密度下，影响似乎并不明显.这一点很容易理解，在较低的车流密度下，车道上留有大量的空隙足以容纳因反应时间延长而引起的刹车距离延长.在较高的车流密度下，车道上存在着大量的静止车辆，在当前时刻前车已经静止，后方跟驰的车辆不可能故意主动加速去制造交通事故.

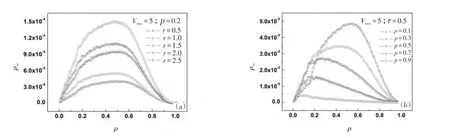
图4 （a）反应时间对交通安全的影响；（b）延迟概率对交通安全的影响Fig.4 （a）Effects of reaction time on traffic safety；(b)Effects of delay probability on traffic safety

图4(b)模拟了不同延迟概率对道路交通安全的影响.车辆发生追尾事故的概率随延迟概率的增加显著减小.同样在较低或较高的车流密度下，影响似乎并不显著.但是频繁刹车导致的后果是交通拥堵严重，整条车道流量急剧下降，如图1(a)所示.

3.3 降低风险的策略

数值模拟揭示了酒后驾驶、疲劳驾驶及不良穿着驾驶等确实导致行车风险剧增，增加延迟概率、限速等方式对降低这些风险确实有一定的帮助，但这是以牺牲道路通行能力及增加车辆磨损为代价的.

图5(a)模拟了不同延迟概率对道路交通安全的影响，结果显示车辆发生追尾事故的概率随延迟概率的增加显著减小.但是频繁的刹车会导致发动机的使用寿命降低、刹车片磨损加剧、油耗增加等问题，严重影响车辆的使用寿命.一般直觉认为：限速可以提高交通安全保障.本文的数值模拟结果也证实了这一点.在图5(b)中，在较低的车流密度ρ＜0.24，对最大速度的限制，提高了交通的安全性.但是，在0.24＜ρ＜0.56这一中等密度区域出现了反常行为.

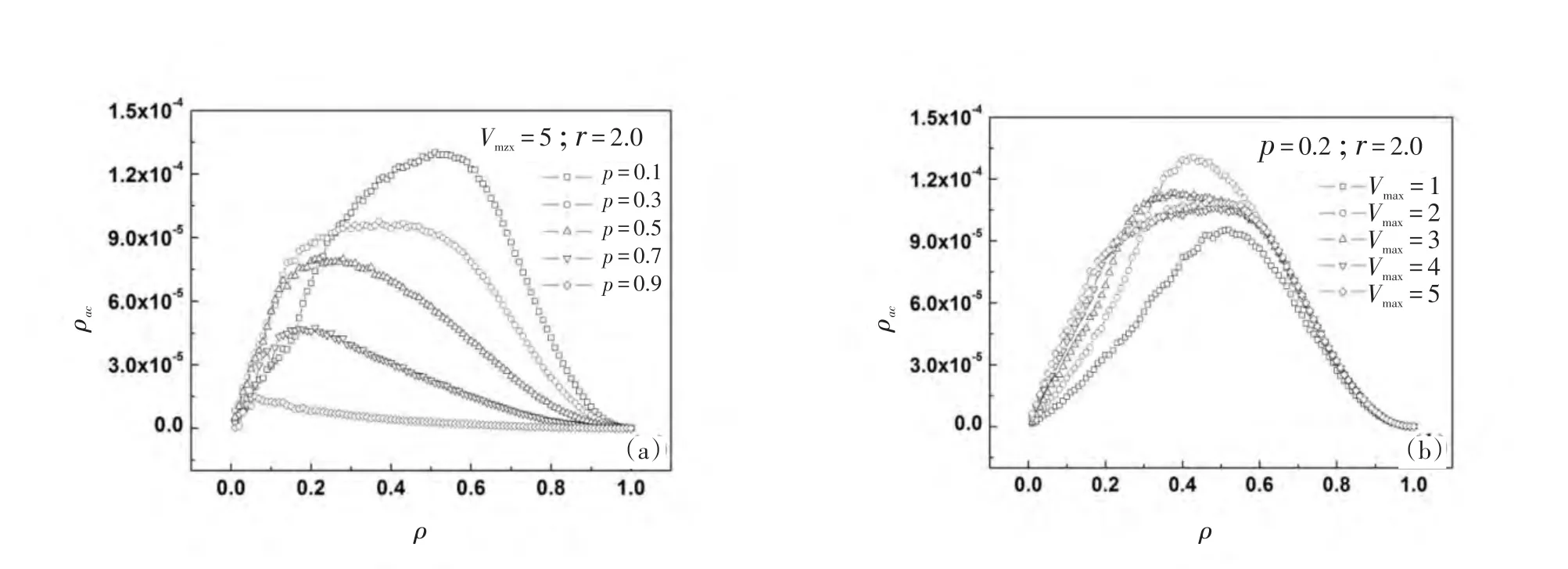
图5 （a）延迟概率对交通安全的影响；（b）限速对交通安全的影响Fig.5 （a）Effects of delay probability on traffic safety；(b)Effects of velocity limit on traffic safety

为了给这反常行为做一定性的解释，图6画出了在 ρ=0.4时，不同的速度极限下车辆的时空演化图.观察图6(a)发现车道上静止的车辆极少，只存在零星的堵塞（黑色的区域），且堵塞随着时间的推移很快消散.图6(b)堵塞区域明显增加.但是和图6(c,d)比较起来，堵塞区域还是相对较小的.图6(c)和图6(d)的堵塞区域没有显著的差别.由安全行车条件可知：运动的车辆才可能存在安全隐患.因此可以定性的认为，在ρ=0.4时，车辆的安全隐患由低到高的顺序是：(Pac)Vmax=4≈ (Pac)Vmax=5＜(Pac)Vmax=3＜(Pac)Vmax=2.这样的结论与图5（b）的模拟结果完全吻合.在现行的交通法规中，对行驶于高速公路的车辆既设定速度上限也设定速度下限.本文的结论是否可以对其做出解释，值得进一步研究.

图6 p=0.2时，车辆的时空演化图.（a）Vmax=2；（b）Vmax=3；（c）Vmax=4；（d）Vmax=5Fig.6 The evolution diagram of position and time whenp=0.2.（a）Vmax=2；（b）Vmax=3；（c）Vmax=4 ；（d）Vmax=5

4 研究结论

酒后驾驶，疲劳驾驶等不良行为是造成行车安全隐患的重要因素.由于驾驶员不良驾驶行为诱发的交通事故具有不可操作性，现场模拟成本高昂，且无法预测其它未显现的驾驶行为对交通安全的潜在危害，因此当前主要的研究模式只能是对已发生的交通事故进行统计分析.本文提出的模型，能重现实际交通中存在的安全风险，可以定量地预测某些不良驾驶行为的后果，进一步揭示严禁酒驾、疲劳驾驶的必要性，以及规范的驾驶行为对保障交通安全的意义.然而，要杜绝酒驾和疲劳驾驶是一项长期而艰巨的任务，不可能一蹴而就，除了强制执行外，还要进行长期的安全教育及法律教育.

[1]贾斌,李新刚,姜锐,等.公交车站对交通流影响模拟分析[J].物理学报,2009,58(10):6845-6851.[JIA B,LI X G,JIANG R,et al.The influence of bus stop on the dynamics of traffic flow[J].Acta Phys.Sin.,2009,58(10):6845-6851.]

[2]钱勇生,曾俊伟,杜加伟,等.考虑意外事件对交通流影响的元胞自动机交通流模型[J].物理学报,2011，60(6):060505.[QIANG Y S,ZENG J W,DU J W,et al.Cellular automaton traffic flow model considering influence of accidents[J].Acta Phys.Sin.,2011,60(6):060505.]

[3]梁玉娟,薛郁.道路弯道对交通流影响的研究[J].物理学报,2010,59(08):5325-5331.[LIANG Y J,XUE Y.Study on traffic flow affected by the road turning[J].Acta Phys.Sin.,2010,59(08):5325-5331.]

[4]杨凌霄,赵小梅,高自友,等.考虑交通出行惯例的双向行人流模型研究[J].物理学报,2011,60(10):100501.[YANG L X,ZHAO X M,GAO Z Y,et al.Bi-directional pedestrian flow model with traffic convention[J].Acta Phys.Sin.,2011,60(10):100501.]

[5]付印平,高自友,李克平.固定闭塞系统下列车运行限速区段交通流特性分析[J].物理学报,2007,56(09):5165-5171.[FU Y P,GAO Z Y,LI K P.The characteristic analysis of the traffic flow of trains in speed-limited section for fixed-block system[J].Acta Phys.Sin.,2007,56(09):5165-5171.]

[6]永贵,黄海军,许岩.菱形网格的行人疏散元胞自动机模型[J].物理学报,2013,62(1):010506.[YONG G,HUANG H J,XU Y.A cellular automata model of pedestrian evacuation in rooms with squared rhombus cells[J].Acta Phys.Sin.,2013,62(1):010506.]

[7]Boccara N,Fuks H,Zeng Q.Car accidents and number of stopped cars due to road blockage on a one-lane highway[J].Journal of Physics A:Mathematical and General,1997,30(10),3329-3332.

[8]Huang D W,Tseng W C.Mean-field theory for car accidents[J].Phys.Rev.E,2001,64(5),057106.

[9]Moussa N.Dangerous situations in two-lane traffic flow models[J].International Journal of Modern Physics C,2005,16(07):1133-1148.

[10]Jiang R,Wu Q S.Dangerous situations in a synchronized flow model[J].Physica A,2007,377:633–640.

[11]Mhirech A,Ez-Zahraouy H,Ismaili A A.Effect of damaged vehicle evacuation on traffic flow with open boundaries[J].Phys.Rev.E,2010,81(1),011132.

[12]Caliendo C,Guglielmo M L D,Guida M.A crash-prediction model for road tunnels[J].Accident Analysis＆Prevention,2013,55:107-115.

[13]Nagel K,Schreckenberg M.A cellular automaton model for freeway traffic[J].J Phys I,1992,2:2221-2229.

[14]Li X B,Wu Q S,Jiang R.Cellular automaton model considering the velocity effect of a car on the successive car[J].Phys.Rev.E,2001,64:066128.

[15]Moussa N.Car accidents in cellular automata models for one-lane traffic flow[J].Phys.Rev.E,2003,68:036127.

[16]Wagner P.Traffic and granular flow[M].Singapore:World Scientific,1996.