关于斜Laplace分布与Levy偏稳定分布的性质

陈明明，马江洪，杨 楠

（长安大学a．经济与管理学院；b．理学院；c．信息工程学院，陕西 西安 710064）

关于斜Laplace分布与Levy偏稳定分布的性质

陈明明a，马江洪b，杨 楠c

（长安大学a．经济与管理学院；b．理学院；c．信息工程学院，陕西 西安 710064）

目前有关重尾或偏态数据的统计分析和理论模型相对较少，基于传统的Laplace分布，提出一种处理偏态和重尾数据的新模型——斜Laplace分布，以研究其参数估计方法。利用数理统计知识推导出该分布与一些常见分布（如正态分布、指数分布）间的统计关系，并给出一种可通过设置不同参数值得到不同分布的Levy偏稳定分布及其稳定性。

斜Laplace分布；MLE估计；Levy偏稳定分布

一、引 言

由于分布是对数据的一个描述，而在现实生活中存在着大量的重尾或偏态数据，因此在统计建模以及对实际生活的数据处理中往往需要更灵活的概率分布。例如可用Kafadar所提出的基于正态分布的一元标准斜正态分布来处理数据中的重尾性，即由服从标准正态分布的随机变量与独立的均匀分布随机变量的比值构造而来，记作X～SLN（q），其中X＝Z／（U1／q），q＞0，随机变量Z～N（0，1），U～U（0，1），且两变量相互独立［1］510－511。

此分布为一个对称分布，且尾部比正态分布的尾部重，因此能很好地应用到重尾数据的拟合中。Mosteller、Rogers分别研究了这个分布的一般性质，且Getnon将Kafadar所提出的一元斜正态分布推广到了多元的情形［2］135－162［3－4］；Tan在t分布的基础上分别介绍了斜t和偏斜t分布，并研究其性质［5］；吴刘仓等人研究了缺失偏态数据下线性回归模型的参数估计问题［6］。笔者在陈明明等人提出的斜Laplace这一新分布的基础上，将进一步研究此分布的参数估计方法和相关的统计性质。

二、斜Laplace分布

（一）参数估计

下面利用矩法及最大似然法对斜Laplace分布的参数进行估计。

在用最大似然方法做参数估计时，采用了两种算法：一是通过解非线性方程组得到估计值，采用此解法是将方程组转化为最小二乘问题，从一个初值开始，搜索方向为Levenberg－Marquardt（L－M）的算法；二是遗传算法（Genetic Algorithm，GA），这是一类借鉴生物界的进化规律（适者生存，优胜劣汰遗传机制）演化而来的随机化搜索方法，主要特点是直接对结构对象进行操作，不存在求导和函数连续性的限定；具有更好的全局寻优能力；采用概率化的寻优方法能自动获取和指导优化的搜索空间，自适应地调整搜索方向，不需要确定规则，而传统优化算法是从单个初始值迭代求最优解的；容易误入局部最优解，而遗传算法对搜索空间中的多个解进行评估，减少了陷入局部最优解的风险，同时算法本身易于实现并行化。

利用上述两种算法进行最大似然估计和矩估计，得到结果见表1。

表1 斜Laplace分布的参数估计表

从表1中可以看出，μ和σ中每个参数的矩估计和最大似然估计都很接近。

（二）与斜Laplace相关的分布

三、Levy偏稳定分布

Levy偏稳定分布常用于分析临界行为和金融数据中，同时在光谱学的分析中也被广泛应用。除了对于α＝2时的正态分布以外，稳定分布都是重尾分布。

一个Levy偏稳定分布是由4个参数所控制的分布，具体定义如下：

（一）稳定性

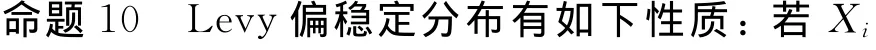
（二）特殊形式

通过观察Levy稳定分布的特征函数φ（t），可以得出以下三种特殊情形：

从中可以看出Cauchy分布、正态分布以及Levy分布都是Levy偏稳定分布中参数取不同值时的特殊情形。

四、结 论

本文针对处理重尾或者有偏数据的新分布——斜Laplace分布，研究其参数估计方法以及与常见分布之间的关系，通过这些关系揭示出了构造斜Laplace分布的不同方法，并通过设置Levy偏稳定分布中不同的参数值，将正态分布、Cauchy分布及Levy分布联系在一起。

［1］ Kafadar K．Slash Distribution［M］．Encyc lopedia of Statistical Sciences，New York：Wiley，1988．

［2］ Mosteller F，Tukey J W．Data Analysis and Regression［M］．Reading MA：Addison－Wesley，1977．

［3］ Rogers W H，Tukey J W．Understanding Some Long-Tailed Symmetrical Distributions［J］．Statist．Neerlandica，1972．

［4］ Genton M G，Wang J．The Multivariate Skew-Slash Distributions［J］．Journal of Statistical Planning and Inference，2006（1）．

［5］ Tan Peng．The Slash and Skew-Slash Student t Distributions［J］．Submitted to Elsevier Science，2005．

［6］ 吴刘仓，张家茂，邱贻涛．缺失偏态数据下线性回归模型的统计推断［J］．统计与信息论坛，2013（9）

［7］ 陈明明，马江洪，吴田军．斜t分布与斜Laplace分布［J］．数理统计与管理，2014（1）．

［8］ Simon M K．Probability Distributions Involving Gaussian Random Variables ［M］．New York：Kuwer Academic Publishers，2002．

［9］ Kozubowski T，Podgórski K，Samorodnitsky G．Tails of Levy Measure of Geometric Stable Random Variables ［J］．Extremes，1998（1）．

［10］Nolan J P．Stable Distributions：Models for Heavy-Tailed Data［M］．Boston：Birkhauser，2009．

［11］茆诗松，程依明，濮晓龙．概率论与数理统计教程 ［M］．北京：高等教育出版社，2004．

On the Properties of the Slash Laplace Distribution and the Levy Skew Stable Distribution

CHEN Ming-minga，MA Jiang-hongb，YANG Nanc
（a．School of Econcmics and Management；b．College of Science；c．School of Information Engineering，Chang＇an University，Xi＇an 710061，China）

In the present，there are few studies focused on statistical analysis and theoretical models for heavy－tailed or skewed data．Based on the classical Laplace distribution，we propose a new model，called slash Laplace distribution，to deal with such data，develop its parametric estimation methods，and establish the statistical relationships between the slash Laplace distribution and several common （e．g．，normal，exponential）distributions by the knowledge of mathematical statistics．Levy skew stable distribution and its stability property are introduced by setting different parameters which can result in different distributions．

slash Laplace distribution；maximum likelihood estimation；Levy skew stable distribution

O212．1∶F222

A

1007－3116（2014）07－0016－06

2014－03－07；修复日期：2014－05－15

国家自然科学基金项目《GIS若干不确定性问题的新刻画及其应用研究》（41071247）；国家自然科学基金项目《模糊假设的统计检验理论和方法研究》（11261044）

陈明明，女，山东枣庄人，博士生，研究方向：运输统计分析；

马江洪，男，陕西绥德人，教授，研究方向：数据挖掘的统计学方法；

杨 楠，男，河南洛阳人，博士生，研究方向：图像处理和机器学习。

（责任编辑：郭诗梦）