全隐式龙格库塔法求解点堆动力学方程
王伟吉,叶金亮,方成跃
(1.海军装备部,北京 100071;2.中国舰船研究设计中心,湖北 武汉430064)
在反应堆动力学和反应堆安全分析中,必 须利用中子动力学方程对中子增殖进行计算。由于点堆中子动力学方程组是一个耦合的刚性一阶微分方程组,求解困难;而且实际动力堆运行时,反应性温度反馈系数不能被忽略,这给反应堆安全分析和运行现场的实时计算等带来了很大的难度。因而,寻求一种高效、实时的数值方法来求解点堆动力学方程组就很有必要。围绕着点堆动力学方程组的刚性问题,国内外学者发展了众多的数值解法,主要有(1)线性多步法,比如 GEAR法、改进 GEAR 法[1];(2)分段多项式逼近法,如拉格朗日插值型和埃尔米特型[2,3];(3)基于积分方程的各种方法,如变量隐含积分法、Hansen方法[4];(4)权重限制法;(5)外推和修匀技巧;(6)有限元法[5];(7)泰勒级数展开法[6];(8)幂级数法[7];(9)指数基函数法[8]。
以上介绍的数值方法中,GEAR法和分段多项式逼近法计算精度较高,但GEAR方法较费时,而分段多项式法计算工作量较小,较省时间,但有时需把步长取得非常小,否则会带来较大的误差,这也导致计算时间拉长[9]。改进GEAR方法稳定域要比GEAR方法大,对步长要求不是那么苛刻,但是计算量较大,比较费时。
另外,幂级数法、指数基函数法计算速度较快、精度较高,适用性较强。
该文研究的基于高斯-勒让特求积公式节点的全隐式龙格库塔法,克服了点堆中子动力学方程组的刚性,保证了数值计算结果的稳定性和精确性,而且计算速度较快,计算过程简捷,易于编程实现。
1 基于高斯-勒让特求积公式节点的全隐式龙格库塔法
不考虑外加中子源的S组缓发中子的点堆中子动力学方程组为
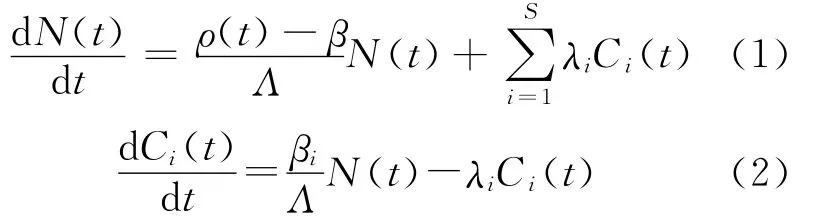
式中,i=1,2,Λ,S;N(t)为中子密度,cm-3;t为时间,s;ρ(t)为反应性;β为缓发中子总份额;βi为第i组缓发中子份额;λi为第i组缓发中子先驱核衰变常数,s-1;Λ 为中子代时间,s;Ci(t)为第i组缓发中子先驱核平均浓度,cm-3;S为缓发中子先驱核组数。
将上述方程组表示为矩阵形式,有:

其中,Y(t)=[N(t),C1(t),Λ,CS(t)]T
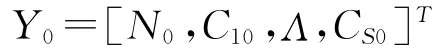
F(t)表示为如下(S+1)×(S+1)阶矩阵:
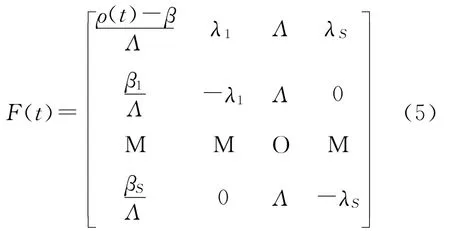
由于F(t)为非常系数矩阵,且是病态的,因此式(3)是刚性方程。在热堆线性反应性引入、快堆阶跃反应性加入、快堆负线性反应性加入等输入条件下,F(t)是强刚性的,求解式(3)非常困难。式(3)的全隐式龙格库塔法求解形式为
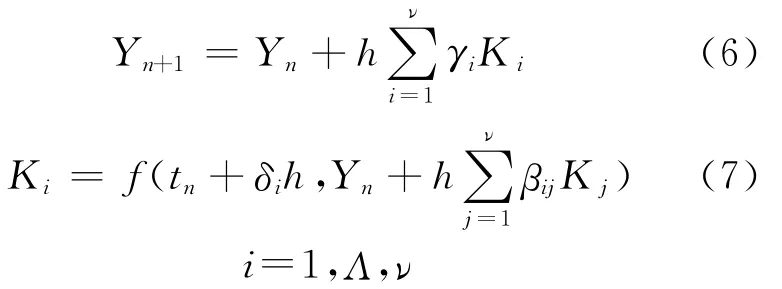
式中,h为计算步长,单位s;ν是GLFIRK方法的节点数,δi为GLFIRK方法的GL节点,γi为权系数,B=(βij)(i,j=1,Λ,ν)为 GLFIRK方法的系数矩阵,f(t,Y)代表式(3)右端式子。令与式(7)联立后可得
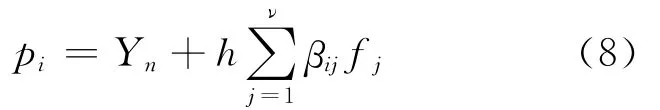
式(8)中,fj=(tn+δjh,pj)
这样,对式(8)进行推理、化简可得
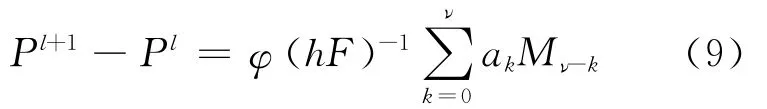
其中,
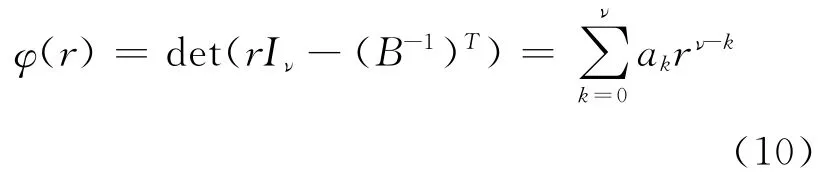
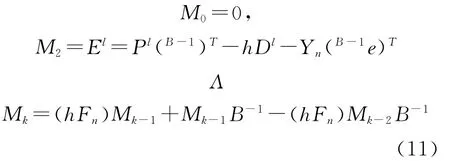
在式(9)、式(10)、式(11)中,r为矩阵(B-1)T的特征值,Iν为ν阶单位矩阵,l为迭代次数,e=(1,Λ,1)T∈Rν,P=(p1,Λ,pi,Λ,pv),D=(p1,Λ,pi,Λ,pv)。
因此,由式(9)可迭代计算出Pl+1,那么
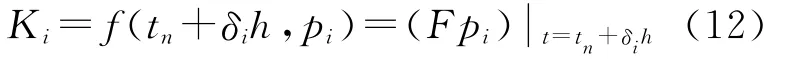
将式(12)代入式(6)即可求得每步的数值解。
表1给出三级六阶GLFIRK法系数,具体推导过程可参阅文献[10]。另外,文献[10]指出GLFIRK是B稳定的,并给出了证明过程,这里不再赘述。
该文以三级六阶GLFIRK方法求解点堆动力学方程,并用MATLAB编制了计算程序,程序简单实用,计算速度快。
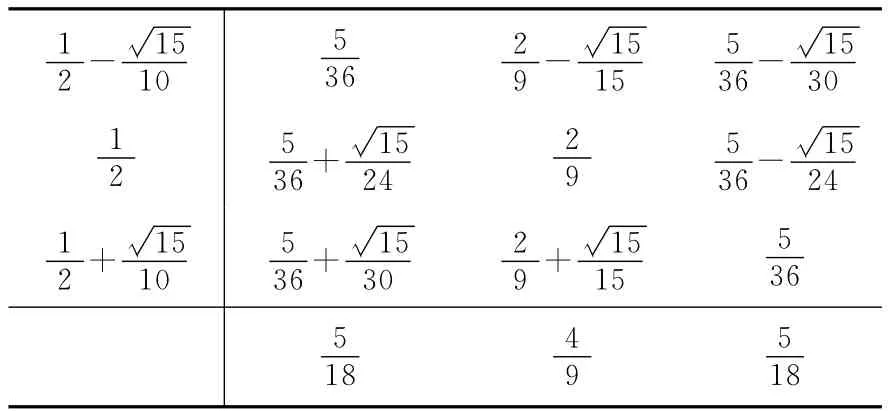
表1 三级六阶GLFIRK方法系数Table 1Three stages six orders GLFIRK coefficients
2 计算实例
例1[11]计算阶跃正反应性输入后热堆内中子密度N(t)随时间的变化。热堆参数为βi:2.66×10-4;1.491×10-3;1.316×10-3;2.849×10-4;8.96×10-4;1.82×10-4;λi:0.012 7;0.031 7;0.115;0.311;1.4;3.87;中子代时间Λ=2.0×10-5缓发中子总份额β=0.007,输入阶跃正反应性ρ=0.003;N(0)=1.0cm-3;计算1s内中子密度随时间的变化。计算结果如表2所示。表2第二列为解析解,其余三列为不同时间步长下由GLFIRK方法求解的数值解,最后一行表示计算得到收敛解CPU所需总时间(Intel Core2Duo CPU E7500@2.93GHz)。由表3可以看出,步长h=0.005s时数值解与精确解吻合得很好,基本保持七位有效数字一致,而h=0.1s时较差。另外,随着时间步长的增加,计算得到收敛解CPU所需总时间在快速减少。步长取得越小,求解得到的数值解精度越高,越接近解析解,与此同时,所需计算时间就越长。因此,在满足一定精度要求的条件下,可适当增加时间步长,这样可以缩短计算时间,以满足实时性要求。
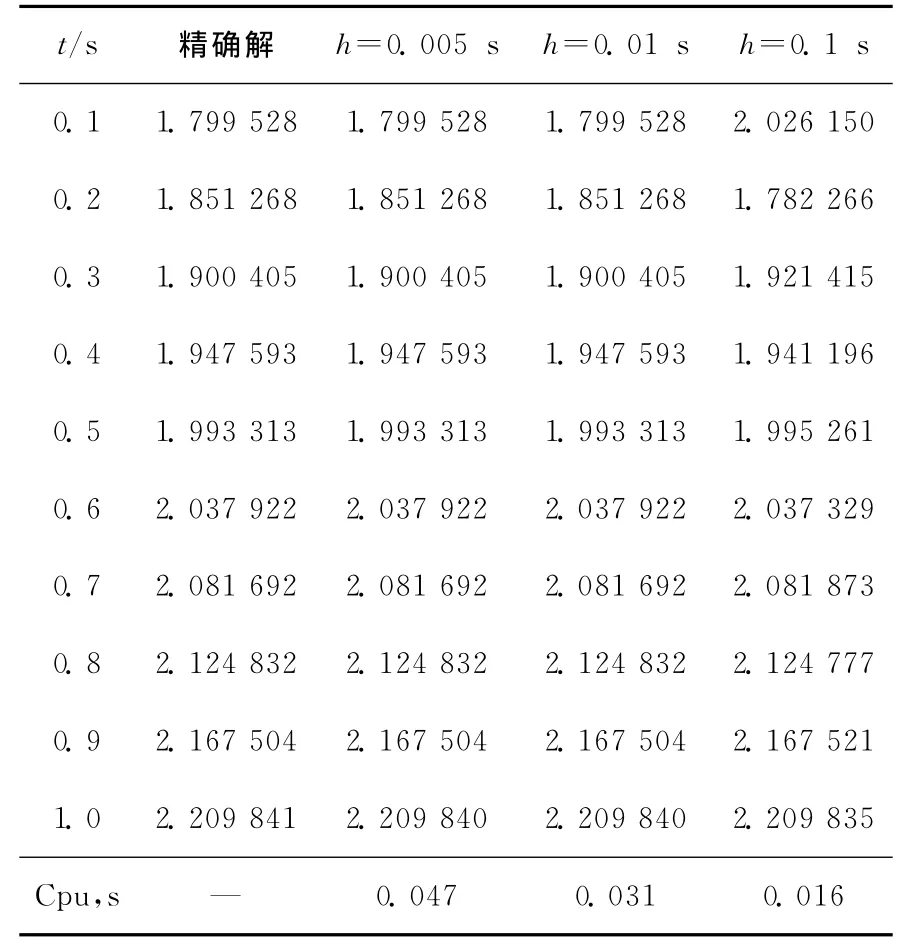
表2 阶跃正反应性输入热堆中子密度N(t)随时间变化Table 2 Neutron densityN(t)v.s.Time with positive step reactivity insertion in thermal reactor
例2计算大正反应性输入后,在瞬发临界的情况下,热堆内中子密度随时间的变化。输入的 正 反 应 性ρ=β=0.007,N(0)=1.0cm-3,计算1s内中子密度随时间的变化,热堆参数同例1。计算结果如表3、表4所示。表3第二列为解析解,其余三列为不同时间步长下由GLFIRK方法求解的数值解。表4为不同时间步长下数值解与精确解之间的相对误差。相对误差100%,由表4可知,随着计算步长的增大,相对误差在增加,而计算时间在缩短。另外,对于大正反应性输入,点堆动力学方程刚性已不明显,但GLFIRK方法仍能在大步长条件下(h=0.1s)将计算精度维持在10-4,由此可见GLFIRK方法求解非刚性微分方程时计算步长的选取范围较之解刚性微分方程要宽些。

表3 大正反应性输入热堆中子密度N(t)随时间变化Table 3 Neutron densityN(t)v.s.Time with great positive reactivity insertion in thermal reactor
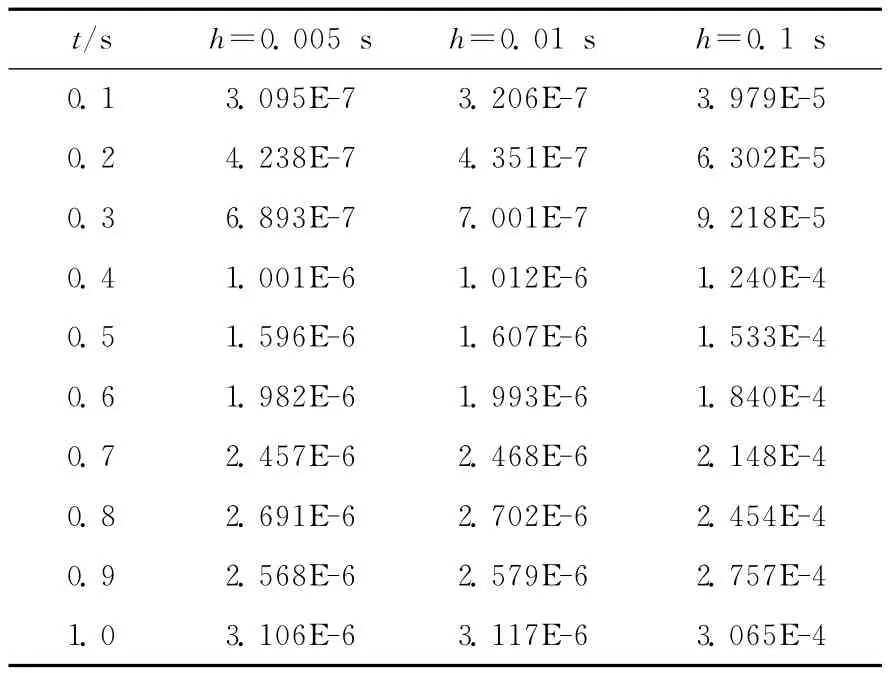
表4 不同时间步长下的相对误差Table 4 Relative Error in different Time step
例3计算阶跃负反应性输入后,堆内中子密度随时间的变化。输入的负反应性ρ=0.007,N(0)=1.0cm-3,计算1s内中子密度随时间的变化,热堆参数同例1。计算结果见表5。表5第二列为精确解,其余三列为在不同计算步长下由GLFIRK计算得到的数值解,最后一行为不同计算步长下GLFIRK计算所花时间。由表5可知,在步长较小时,数值解与精确解吻合的相当好,但在大步长下数值解较之精确解出现很大偏差,有些数值甚至是错误的。可见,在阶跃负反应性输入时,点堆方程刚性较强,这时GLFIRK计算步长宜取较小值,以满足精度要求,否则会出现较大偏差甚至错误数值。

表5 阶跃负反应性输入热堆中子密度N(t)随时间变化Table 5 Neutron density N(t)v.s.Time with negative step reactivity insertion in thermal reactor
例4计算线性反应性输入后,热堆中子密度随时间变化。输入的反应性ρ=0.000 7t,N(0)=1.0cm-3,计算10s内中子密度随时间的变化。热堆参数同例1。计算结果见表6、图1。表6第二列为精确解,其余三列为不同时间步长下由GLFIRK方法求解的数值解,最后一行为不同计算步长下GLFIRK所花时间。图1中相对误差的对数值是取10为底的对数值。
由表6、图1可知,在步长较小时,数值解非常接近精确解,而当计算步长逐步增大时,相对误差快速增加,严重偏离解析解,此时计算发散。因此,在线性反应性输入时,点堆方程刚性很强,此时,GLFIRK宜取较小的时间步长以保证计算精度,但这样就增加了计算时间,实时性较差。

表6 线性反应性输入热堆中子密度N(t)随时间变化Table 6 Neutron density N(t)v.s.Time with positive ramp reactivity insertion in thermal reactor

续表
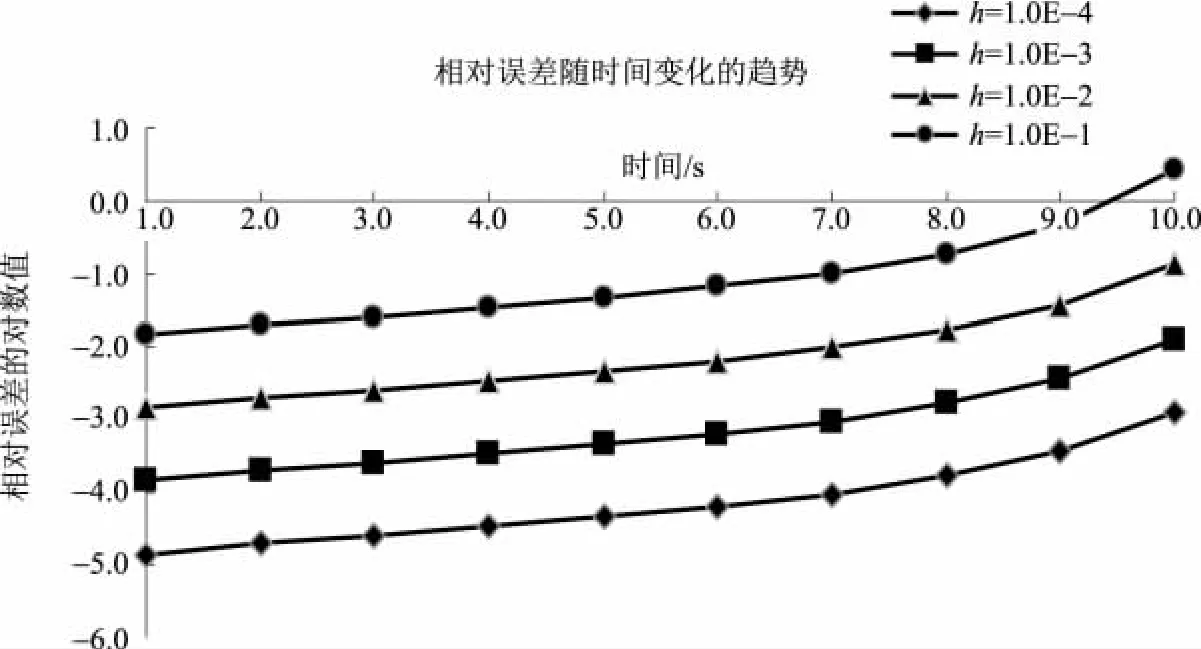
图1 不同时间步长下的相对误差曲线Fig.1 Relative Error Curve in different time step
例5计算正弦反应性输入后,热堆中子密度随时间的变化。ρ=ρ0sin(πt/T),T为输入正弦反应性的周期,s,ρ0为反应性幅度,热堆参数同例1。计算结果见表7、图2。由表7可以看出,GLFIRK方法能准确地计算出峰值及其对应的时间,而且当其步长为Hermite方法的100倍时仍能保证5~7位有效数字相同。图2为ρ0=0.2β,T=5s时的正弦反应性输入后中子密度随时间的变化规律。从图2可以看出,中子密度随时间的增长不停地振荡,振幅逐渐加大,该结果与文献[13]得出的结论一致。
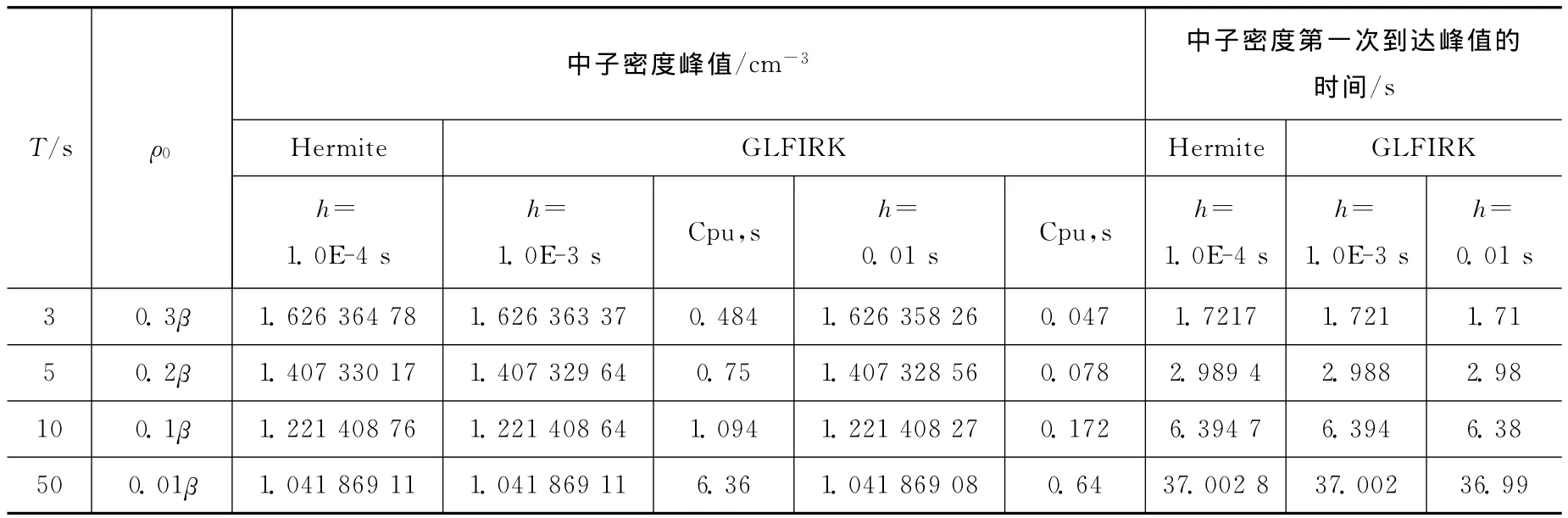
表7 正弦反应性输入热堆中子密度N(t)峰值及其对应时间Table 7 Peak of Neutron DensityN(t)and Corresponding Time with Sinusoidal Reactivity Insertion
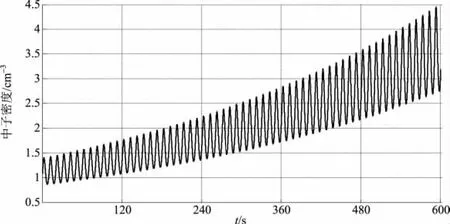
图2 正弦反应性输入后中子密度随时间的变化Fig.2 Neutron Density v.s.Time with Sinusoid Reactivity Insertion
3 结论
该文用GLFIRK方法在热堆、快堆的典型反应性输入条件下对点堆动力学方程进行求解,求解结果表明该方法的计算精度很高、计算速度较快、适应能力较强,满足一定的工程应用要求。主要有以下几点结论。
(1)对于刚性不显著或者非刚性情况,如热堆阶跃小正反应性引入、阶跃大正反应性引入,GLFIRK方法能满足计算精度和实时性要求,从例1、例2的计算结果可以看出。
(2)对于刚性显著的情况,如热堆阶跃负反应性引入,GLFIRK方法仍能满足计算精度和实时性要求,从算例3的计算结果可以看出。此时,计算步长不宜取大值,以h=0.001s为宜,这时可兼顾计算精度和实时性两方面要求。
(3)对于刚性很强的情况,如热堆线性反应性引入,GLFIRK方法不能同时兼顾计算精度和实时性要求,从例4的计算结果可以看出。此时,取步长h=0.001s计算可以得到满足工程应用计算精度的数值,但实时性要差些。
(4)对于复杂反应性引入情况,如正弦反应性引入,GLFIRK方法可以满足计算精度和实时性要求。从例5计算结果可以看出。
综上所述,GLFIRK方法是计算稳定、数值精度较高、适应力较好,可满足一定的工程应用要求。
[1] 肖红,王侃.求解点堆动态方程的IGEAR方法[J].核科学与工程,2008,38(2).
[2] J.P.Hennart Piecewise Polynomial Approximations for Nuclear Reactor Point and Space Kinetics[J].Nuclear Science and Engineering,1977,64:875-901.
[3] Kueng Yeh Polynomial Approach to Reactor Kinetics Equations[J].Nuclear Science and Engineering,1978,66:235-242.
[4] Hansen K.F.,Koen B.V..Little W.W .Stable Numerical Solutions of the Reactor Kinectics Equations[J].Nuclear Science and Engineering,1965,22:51-59.
[5] 赵志远.用有限元法解点反应堆动力学方程[J].原子能科学与技术,1981,15(6):656-663.
[6] 陈昌友.一个新的求解点堆中子动力学方程组的数值方法[J].核科学与工程,1998,18(4):364-370.
[7] Basken J,Lewins J.D.Power series Solutions of the Reactor Kinetics Equations[J].Nuclear Science and Engineering,,1996,122:407-416.
[8] 黎浩峰,陈文振,朱倩,罗磊 .点堆中子动力学方程的指数基函数法求解[J].核动力工程,2009,30(4).
[9] 经荥清,李君利,罗经宇 .点动态方程几种解法的比较[J].清华学报,1995,35(3):7-12.
[10] 李庆杨 .常微分方程数值解法[M].北京:清华大学出版社,1990:87-120.
[11] 胡大璞 .克服点堆中子动力学方程刚性的新方法—端点浮动法[J].核动力工程,1993,14(2).
[12] 濮继龙 .点堆动态方程的半解析解[J].核动力工程,1983,4(1).
[13] Peinetti F.,Nicolino C..Ravetto P.Kinetics of a point reactor in the presence of reactivity Oscillations[J].Ann Nucl Energy,2006,33:1189-1195.

