机舱通风口冲击射流湍流特征分析及验证

刘正先，张冀伸，平 艳

(天津大学机械工程学院，天津 300072)

快捷舒适使得21世纪的人们越来越依赖飞机出行，在高空环境下，机舱内的空气流通和品质成为考核飞行的主要指标．通风口是直接的送风装置，来自送风口的自由射流气体接触到人体和座椅后变为壁面冲击射流，在这一过程中气流的速度以及脉动特征与随后的新、旧空气交换以及交换效果有密切关系．因此，研究射流流场的湍流特征对有效控制和组织舱内气流具有重要意义．

冲击射流一般分为 3个区．①自由射流区.由于剪切应力的作用，射流将周围介质及相应动量、能量裹入到射流中．产生的影响有：非均匀径向速度剖面的发展，冲击到下板前射流温度的改变等．②滞止区.流动在由轴向转为径向之前的区域，定义为径向距离r与喷嘴直径 Dn之比小于 2.0，在此区间内，流动速度迅速滞止为0，并且急剧地由轴向转为径向，产生很大的逆压力梯度．参数变化剧烈，从而使冲击射流表现出与自由射流完全不同的特性．③壁面射流区.在滞止区压力梯度的驱动下，流体迅速向外流出，但已不再是简单的平行剪切流动[1-3]．

冲击射流的湍流特征主要由以下湍流参数体现：在对称线(喷管轴线)附近，为流向应力和流向速度、脉动速度；在壁面平行方向，为切向应力和切向速度、脉动速度；在冲击壁面上，主要为局部换热系数[4-6]．笔者采用数值方法对圆形自由射流和冲击射流流场特征进行模拟并分析湍流模型的适用性，为机舱内通风口附近的复杂射流较准确数值模拟提供可行性支持．

1 数值模型及计算方法

确定 Knowles等[7]的自由+壁面冲击射流作为本文射流计算和射流特征对比的典型算例．分别分析射流流场的无量纲主流速度、脉动速度、雷诺应力等湍流参数，通过与实验对比，确定数值方法和湍流模型对冲击射流流场典型特征的模拟能力．

图1为冲击射流流场及坐标系统．其中3个典型区域为自由射流区、壁面射流区和冲击区．流体在一定的雷诺数下从喷嘴喷出形成自由射流，打到冲击板上形成壁面冲击射流．气流在射流出口处充分发展，属于轴对称流动．

图 2为计算区域及边界条件．喷嘴出口处雷诺数 Re＝9,000(Re＝UinDn/ν)，其中 Uin为射流出口速度，喷嘴入口直径 Dn为 0.025,4,m．喷嘴距离冲击板高度Hn为10倍喷嘴直径．图1中Um、Vm为最大流向和径向速度；U、V为流向和径向速度；r为距离喷嘴轴线的距离，r1/2为速度是 0.5Um时与喷嘴轴线的距离；V1/2为最大径向速度的一半；Y1/2为 0.5Vm时距离冲击板的高度．

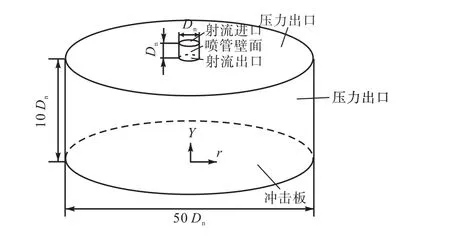
图2 计算区域及边界条件Fig.2 Computation domain and boundary conditions

数值模拟采用雷诺时均流动控制(Reynolds Averaged Navier Stokes，RANS)方程，RANS 方程的张量形式为

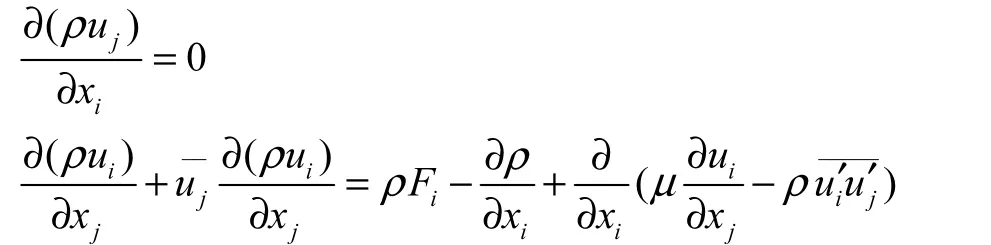
式中：ρ为流体密度；ui为速度分量；xi为坐标系分量；Fi为质量力，在本计算中质量力为重力；μ为动力涡黏系数．

式中：ijδ为克罗内克符号；tμ为湍流涡黏系数，是确定 Reynolds应力的关键．本文采用了3种 k-ε 湍流模型定义涡黏系数，并与 k-ω 模型和大涡模拟(LES)的计算结果对比，通过分析各湍流模型的准确度和局限性，确定最适合的一种进行较细致的射流流动分析．

标准k-ε 模型涡黏系数定义为

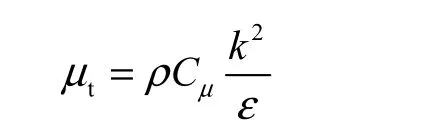
式中k、ε分别为湍动能和湍流耗散率[8]．

计算采用的另外两种湍流模型是Rng k-ε 模型和Relizable k-ε 模型．前者通过从控制方程中引入旋转相关项，并在ε 方程中添加时均应变率项来体现流动的高应变率及弯曲率的影响．后者则对湍动黏度做修改，即 Cμ= 1 (A0+ AsU∗k/ε)，其中 A0和 As为修正系数．k-ω 模型与 k-ε 模型的区别是用涡量方程代替ε方程．上述湍流模型和 LES的详细关系式参见文献[9-11]．

计算域网格如图3所示，在冲击板附近的固壁处进行网格加密处理，由固壁处向计算域中间的网格增长率为 1.02，壁面第 1层网格长度为 0.005,m，第 1层网格满足 y+＝12～20．另外在冲击板附近流动变化较剧烈区域局部加密[12-13]．

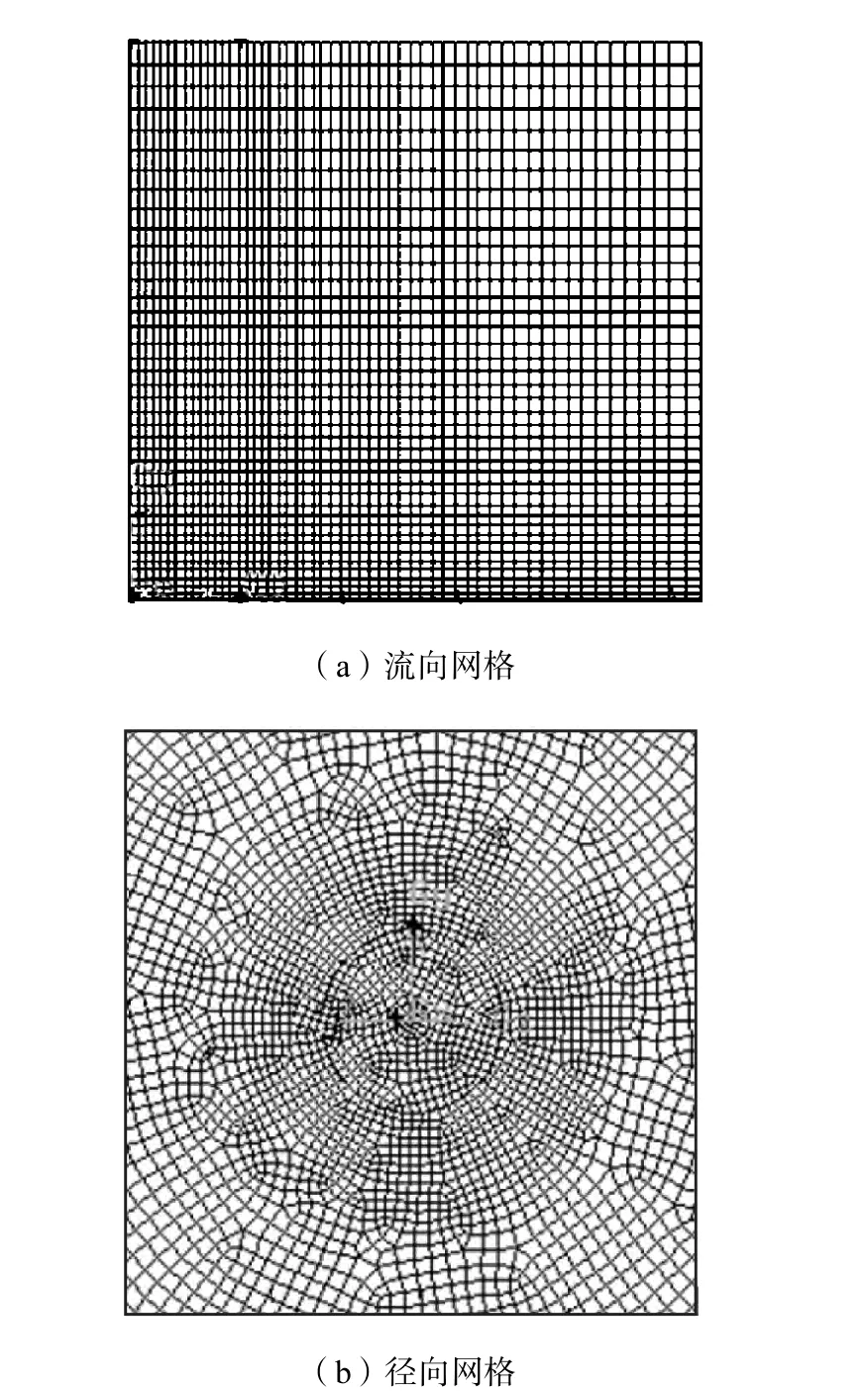
图3 Hn/Dn＝10冲击板射流流向和径向网格布置Fig.3 Mesh in axial and radial direction(Hn/Dn＝10)

计算流动介质为不可压缩空气．边界条件：计算域四周及上边界为压力出口；进口为速度入口；喷嘴管及计算域下边界为绝热固体壁面．

2 结果与讨论

2.1 几种湍流模型和LES的对比

首先对4种湍流模型和LES在射流主流速度方面的模拟能力进行对比．在所有结果图中，数据点为实验数据，线条为数值计算值．图 4为距离冲击板高度分别为 4、5和 8倍直径高度的主流速度与实验值的对比，Hp/Dn代表无量纲高度位置，其中Hp为实验探针距离冲击板的高度．从图 4(a)和图 4(b)中可以看出4种 RANS模型在r r1/2＜ 1 .2区间几乎重合，但超出该区间后，所有 k-ε 模型均好于 k-ω 模型，与实验值更接近，而在 3 种 k-ε 模型中，Relizable k-ε 模型与实验值最符合．相对于RANS模型，LES模型在大部分区间偏差较大，仅在r r1/2＜ 0 .4的射流核心区，比 RANS更接近实验值．图 4(c)更明显地说明了这一点．

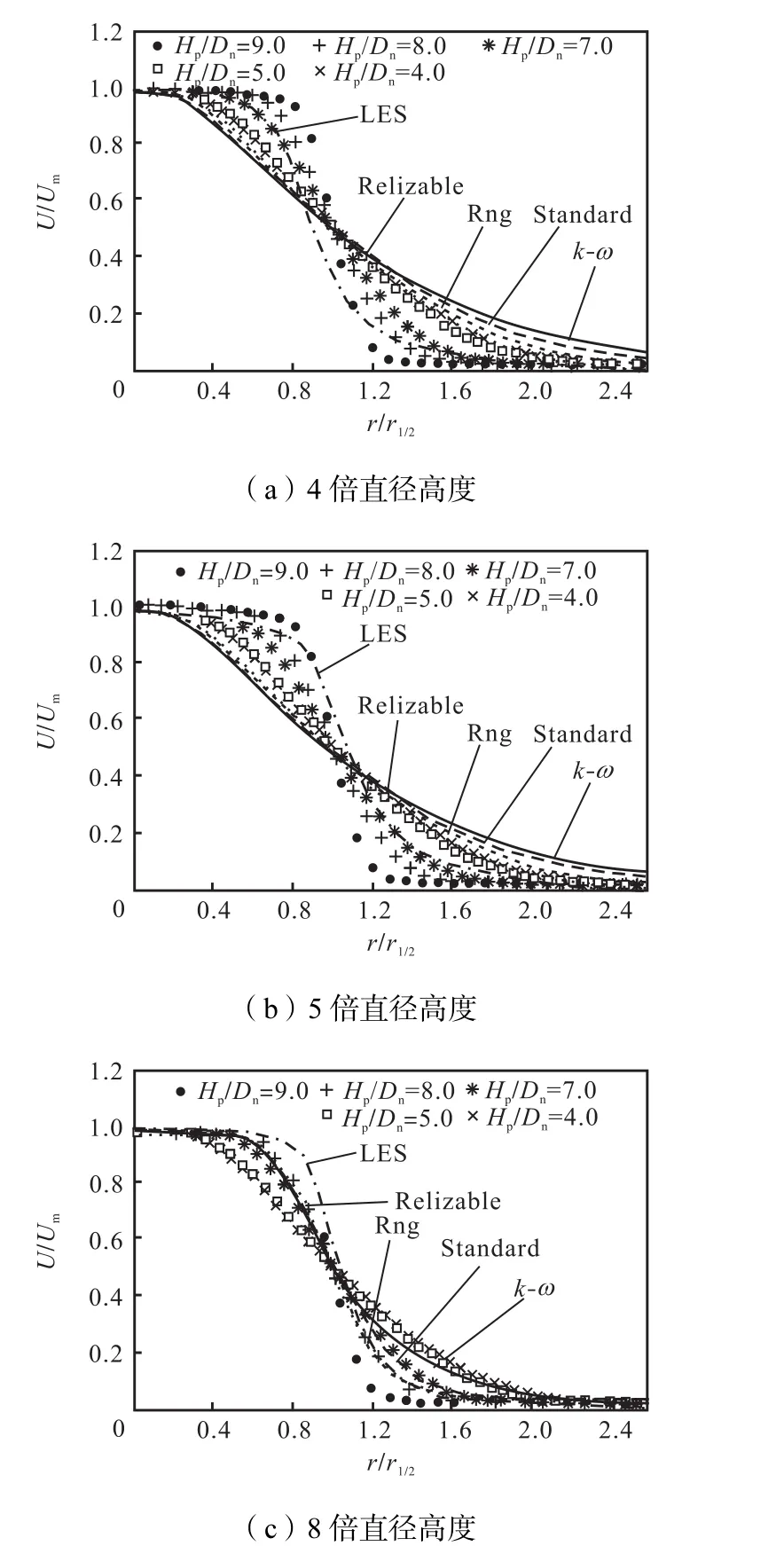
图4 几种湍流模型和LES的主流速度对比Fig.4 Comparison of main velocity between turbulence models of RANS and LES

综合来看，5种模型均模拟出了与实验值一致的速度分布趋势．但 LES明显不如 RANS模型，而RANS模型中Relizable k-ε 无论在冲击板较近区域，还是在冲击板不同高度，均有更好的符合度，兼具了RANS其他 3种模型在 r r1/2＜ 1 .2区间和LES在r r1/2＞ 1 .2区间的优点．因此，决定确立Relizable k-ε模型继续分析射流湍流特征．

2.2 自由射流对比分析

图 5为 Relizable k-ε 湍流模型计算得到的无量纲主流速度分布与实验值的对比(点为实验值，线条为模拟值，下同). U方向的主流速度与实验值整体符合很好，在r r1/2= 0 .8的位置出现快速衰减、r r1/2= 2 .0附近流动发生滞止，数值结果很好地反映了这2个典型流动特征；对于V方向速度，由于在近壁面位置，冲击射流形成流动分离[4]，湍流模型无法预测径向速度的这一变化，因此与实验值在射流核心区(r r1/2＜ 0 .6)存在较大偏差；随着半径方向位置的增大，流场逐渐稳定且与实验很好符合，能准确反映出r r1/2= 2 .0之前发生的流动滞止点，与U方向相应位置吻合．

图5 不同位置自由射流的无量纲平均速度Fig.5 Non-dimension mean velocity of free jet at different positions

本研究中分析比较了 U方向脉动速度 u′以及 V方向脉动速度v′的变化．从图6无量纲湍流脉动速度与实验值对比可以看出，计算值与实验值具有一致的变化趋势，即在 r r1/2= 0 .8出现湍动速度峰值之后衰减．但在冲击板附近的射流核心区，数值结果略低于实验值，此区域为自由射流向壁面射流转变区，在此位置处射流将产生涡的破碎与衰减，流动出现较强的弯曲及旋转[6]，Relizable k-ε 湍流模型在预测此类流动方面还存在局限性，不过随着距离冲击板高度的增大，流动逐渐稳定，这种偏差很快缩小，与实验结果吻合很好．

图 7为雷诺切应力对比图，与脉动速度类似，数值计算峰值点和滞止点与实验结果一致，射流轴线附近接近壁面位置，由于存在浮力、曲率和旋转流动特征[7]，核心区的数值结果略偏高于实验值．

图6 不同位置自由射流无量纲脉动速度Fig.6 Non-dimension fluctuating velocity of free jet at different positions

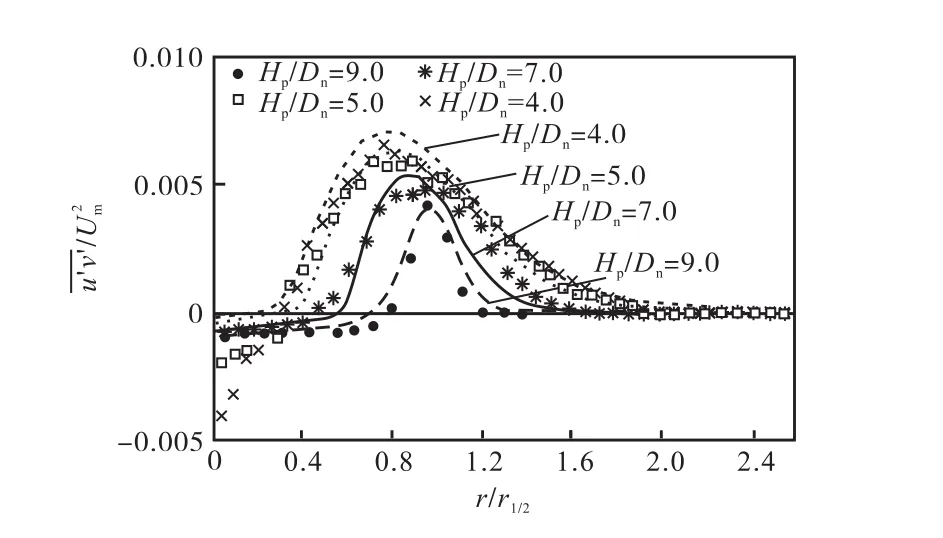
图7 不同位置自由射流区无量纲雷诺剪切应力Fig.7 Non-dimension Reynolds shear stress of free jet at different positions

2.3 壁面冲击射流对比分析

自由射流数值与实验结果的对比表明，采用Relizable k-ε 湍流模型对冲击射流的自由射流区模拟，虽然在近壁面核心区略有偏差，但整体上看与实验结果吻合很好．以下对壁面冲击射流区进行对比．

图8为无量纲速度 U对比结果，rp/Dn代表无量纲径向位置，其中 rp为实验探针与喷管轴线间的径向距离(点为实验值，线条为模拟值，下同)．流向速度预测结果与实验值整体吻合较好，在r r1/2= 0 .8附近出现平均速度峰值，之后逐渐衰减，随着流动发展，速度快速降低为零，流动滞止，实验显示了相同的变化过程．在冲击板上方近壁面处(Y Y1/2＜ 0 .1)，数值结果与实验值存在微小正偏差，但不影响与实验的一致性．

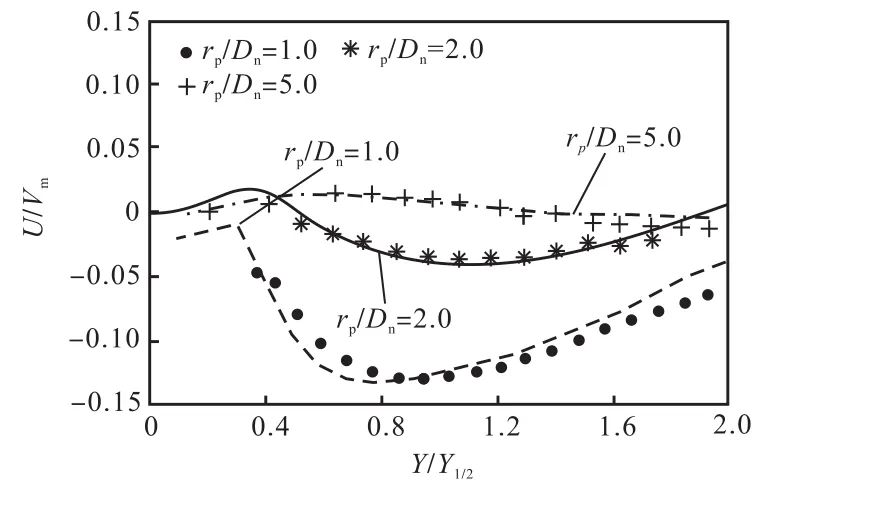
图8 不同位置壁面射流的无量纲主流速度Fig.8 Non-dimension main velocity of wall jet at different positions

图9为流向和径向无量纲脉动速度对比，数值结果与实验值具有高度一致性，准确反映了脉动速度在壁面处的变化特征，包括速度峰值点及滞止区范围．

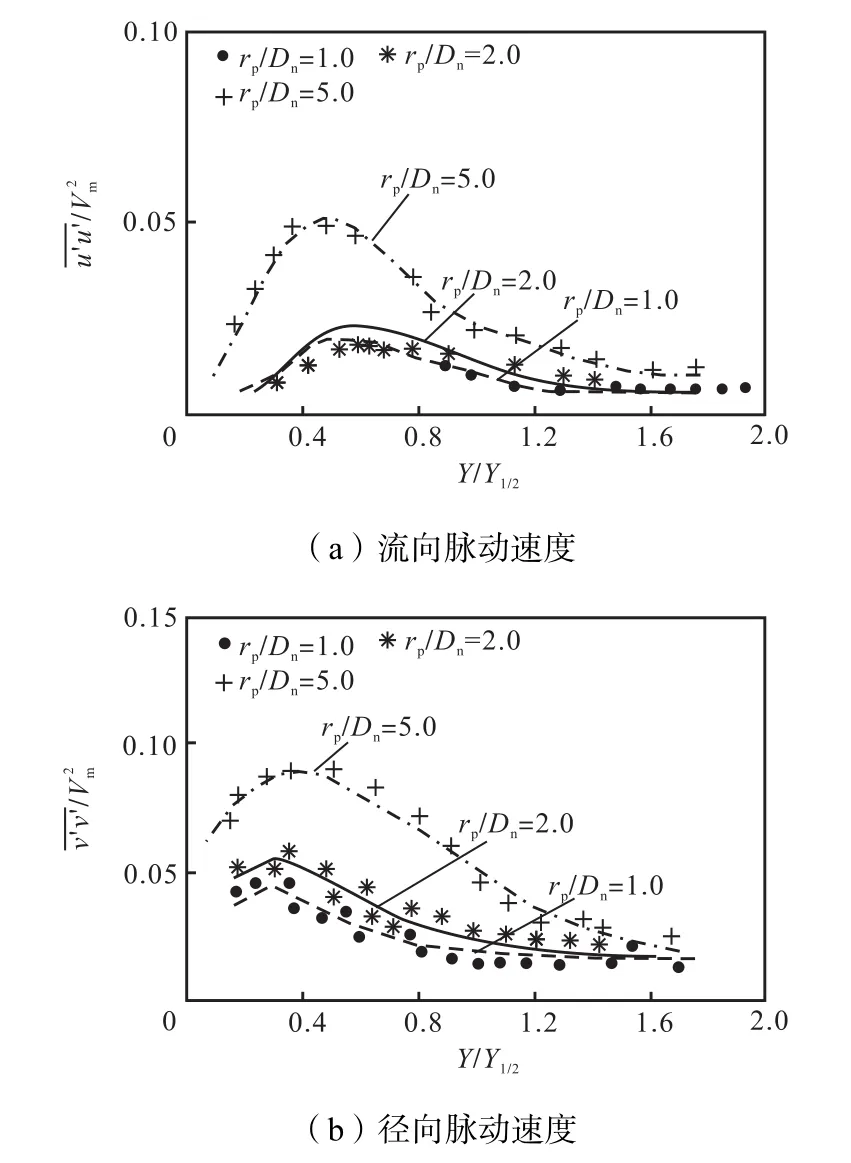
图9 不同位置壁面射流区无量纲脉动速度Fig.9 Non-dimension fluctuating velocity at different positions in the wall jet area

图 10为无量纲雷诺切应力对比．数值结果与实验值整体吻合很好，仅在 Y Y1/2＜ 0 .2即近冲击板位置受到强旋转和弯转流动影响[13]，使得计算略偏移实验值．

综合以上结果可得，采用Relizable k-ε 湍流模型基本可以得到与实验一致的流动特征分布，并能正确模拟出自由射流区、滞止区和壁面射流区．但对自由射流，在冲击板近壁面的射流核心区，由于受流动强弯曲、旋转的影响，与实验在径向主流速度上产生一定正偏差，由此导致相应的脉动强度偏低于实验值．这也是RANS共同存在的问题．

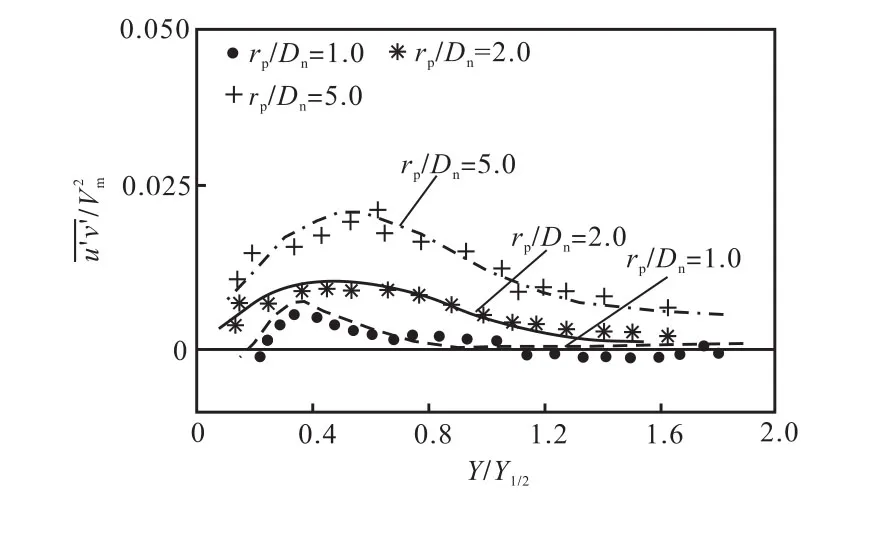
图10 不同位置壁面射流的无量纲雷诺剪切应力Fig.10 Reynolds shear stress of wall jet at different positions

3 结 语

通过对 4种 RANS湍流模型的计算对比，确定Relizable k-ε 湍流模型结果与实验值更接近．该湍流模型在预测自由射流和壁面射流流场的主流速度、脉动速度和雷诺应力方面与实验值具有较好的吻合度，可以获得正确的流场变化特征和演化趋势：主流速度在自由射流区快速衰减、湍动速度在峰值后逐渐衰减．能够准确预测滞止区范围，可为实验测量冲击射流换热系数提供可靠的流场依据．但在距离冲击板更近的射流核心区域，与实验值还是存在一定的偏差．而 LES恰好在射流核心区与实验吻合更好．若能把RANS与LES组合进行冲击射流流动的数值模拟研究，将是实际机舱内局部射流深入研究的最佳策略．

［1］ 刘沛清. 自由紊动射流理论[M]. 北京：北京航空航天大学出版社，2008.

Liu Peiqing.Theory of Free Turbulent Jet[M]. Beijing：Beihang University Press，2008(in Chinese).

［2］ 徐惊雷，徐 忠，肖 敏，等. 冲击射流研究概述[J]. 力学与实践，1999，21(6)：8-17.

Xu Jinglei，Xu Zhong，Xiao Min，et al. On impinging jet research[J].Mechanics in Engineering，1999，21(6)：8-17(in Chinese).

［3］ Jaramillo J E，Pérez-Segarraa C D，Rodrigueza I，et al. Numerical study of plane and round impinging jets using RANS models[J].Numerical Heat Transfer，2008，54(3)：213-237.

［4］ Quinn W R，Militzer J. Experimental and numerical study of a turbulent free square jet[J].American Institute of Physics，1988，31(5)：1-4.

［5］ Slawomir Kubackia，Erik Dick. Hybrid RANS/LES of flow and heat transfer in round impinging jets[J].International Journal of Heat and Fluid Flow，2011，32(3)：631-651.

［6］ 王 维，姜 楠，曹晓东，等. MD-82飞机客舱环境流场的 HWA测量与分析[J]. 天津大学学报：自然科学与工程技术版，2013，46(1)：2-7.

Wang Wei，Jiang Nan，Cao Xiaodong，et al. HWA measurement and analysis of MD-82 aircraft cabin environment flow fields[J].Journal of Tianjin University：Science and Technology，2013，46(1)：2-7(in Chinese).

［7］ Knowles K，Myszkob M. Turbulence measurements in radial wall-jets[J]. Experimental Thermal and Fluid Science，1998，17(1)：71-78.

［8］ 陶文铨. 数值传热学[M]. 西安：西安交通大学出版社，1992.

Tao Wenquan.Numerical Heat Transfer[M]. Xi'an：Xi'an Jiaotong University Press Company Limited，1992(in Chinese).

［9］ Zhang Wei，Chen Qingyan. Large eddy simulation of indoor airflow with a filtered dynamic sub-grid scale model[J]. International Journal of Heat and Mass Transfer，2000，43(17)：3219-3231.

［10］ Wilcox D C. Simulation of transition with a two-equation turbulence model[J]. AIAA Journal，1994，32(2)：1-3.

［11］ 张兆顺，崔桂香，许春晓. 湍流大涡数值模拟的理论与应用[M]. 北京：清华大学出版社，2008.

Zhang Zhaoshun，Cui Guixiang，Xu Chunxiao. Theory and Application of Large Eddy Simulation of Turbulent Flow[M]. Beijing：Tsinghua University Press，2008(in Chinese).

［12］ Anderson J D. 计算流体力学基础与应用[M]. 北京：机械工业出版社，2010.

Anderson J D.Computational Fluid Dynamic[M]．Beijing：China Machine Press，2010(in Chinese).

［13］ Cooper D，Jackson D C，Launder B E，et al. Impinging jet studies for turbulence model assessment(Ⅰ)：Flow field experiments[J].International Journal of Heat and Mass Transfer，1993，36(10)：2675-2684.