钢筋混凝土框架结构地震失效模式优化

李忠献，王 虹，吕 杨，徐龙河

(1. 天津大学滨海土木工程结构与安全教育部重点实验室，天津 300072；

2. 中国建筑设计研究院，北京 100044；3. 北京交通大学土木建筑工程学院，北京 100044)

地震作用下，建筑结构的薄弱层或薄弱区域会先于其他部位出现损伤，如果受损部位的内力和变形没有被相邻构件分担，在持续的地震作用下，损伤将在薄弱部位积累和发展，致使构件的抗震性能退化并最终失效，并且结构关键构件的失效破坏还可能造成整体结构的倒塌，因此，整体结构的抗震性能由结构的薄弱层或薄弱区域控制．若结构所有构件的抗震性能相当，结构不存在薄弱层或薄弱区域，则可以避免损伤在特定部位积累，结构整体的抗震性能得到显著提高，结构材料强度等得到最大程度的利用．基于这种思想，Kim 等[1]通过优化设计结构的强度和刚度以达到结构各层层间位移角相等的目的，其优化方法的有效性通过数值算例进行了验证，但结构各层具有相同的层间位移角并不能保证结构各层具有相同的抗震性能．因此，Hajirasouliha等[2]采用 Park-Ang双参数损伤准则，分别基于质量最轻和损伤最小两种优化方法对钢筋混凝土框架结构进行了优化设计，并提出一种多目标最优的设计方法，结果表明所提出的方法能有效地降低造价、提高结构抗震能力．吕杨[3]提出了一种以钢框架结构层为优化对象的优化方法，结果表明，该优化方法能够有效提高结构的抗震性能，且优化后的钢框架结构用钢量较初始结构有显著的减少．

笔者在文献[3]的基础上，提出一种以结构柱为优化对象的失效模式优化方法，该方法以整体结构的损伤指数为结构优化的约束方程和目标函数，通过修正结构构件参数如截面尺寸、配筋率或材料强度等达到优化结构整体失效模式的目的．并以某 12层钢筋混凝土框架的 Benchmark模型结构为例，通过数值分析验证了新方法的实用性和有效性．

1 失效模式优化设计

结构失效模式优化是在结构损伤准则约束下，对结构各构件的抗震性能进行迭代优化，使结构主要构件具有相近的抗震性能．优化方法需要定义结构的损伤准则、目标函数和迭代过程．结构损伤准则包括材料、构件和整体结构 3个层次，材料层次的损伤准则通过钢材和混凝土的损伤本构模型定义．

1.1 钢材损伤本构模型

Bonora等[4]基于连续性损伤力学提出了钢材的弹塑性损伤本构模型，模型采用非线性损伤演化法则，能够较好地模拟钢材的强度、刚度退化以及失效断裂过程，与已有试验对比分析表明模型具有很高的模拟精度，其损伤发展的基本方程为

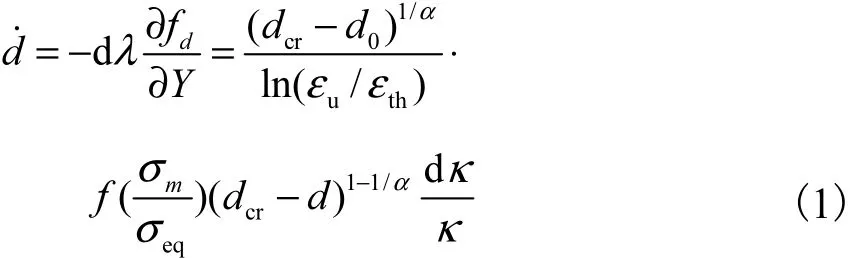
李忠献等[5]结合经典的弹塑性力学理论，将上述损伤模型进行修正提出单轴的 Bonora损伤本构模型，并通过LS-DYNA程序的二次开发将模型植入到有限元主程序中．

1.2 混凝土损伤本构模型

Faria等[6]提出了一种混凝土的弹塑性损伤本构模型，研究表明该模型参数少、标定简单且计算效率高，适用于大型钢筋混凝土结构的地震响应分析，但其在模拟循环荷载作用下混凝土从压到拉的刚度退化规律时效果欠佳．李正等[7]通过引入一个刚度影响因子来描述循环荷载作用下混凝土的单边效应，修正了原模型的缺陷，并基于混凝土 Faria-Oliver多轴损伤本构模型提出了适用于纤维单元模型的修正Faria-Oliver损伤本构模型．模型的拉、压损伤演化方程为

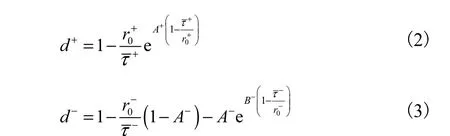
式中：A+、A-、B-为模型参数；0r+、0r-为拉、压损伤阈值的初始值．

1.3 结构损伤准则

采用纤维单元模型模拟地震作用下结构动力响应的方法能够以较低的计算成本获得很高的求解精度，本文采用针对纤维单元模型定义的钢筋混凝土框架结构构件、结构层以及整体结构的损伤准则对结构进行优化．

将框架结构按照柱构件所处的位置、截面尺寸以及纵筋的配筋率等指标进行分类，并假定各类柱构件的抗震性能相同．将框架结构第j层第i类柱构件的损伤指数定义为

采用式(4)得到柱构件的损伤指数后，由于结构每层各类柱以并联的方式连接，将框架结构层的损伤指数(damage index，DI)定义为该层各类柱构件按照构件重要性指数[8]的加权平均值，即

式中：jD为框架第j层损伤指数；ijω为第j层第i类柱构件的重要性系数；,ijkfΔ为拆除结构第j层第i类柱构件中的任一柱构件后，剩余结构第k阶频率增量；fk为原始结构第k阶频率．计算时，应保证所取结构频率对应的模态质量之和不小于结构等效质量的90%.

得到结构各层的 DI后，由于整体结构是由各层串联形成，定义框架结构整体的损伤指数gD为所有结构层中所具有的最大损伤值，即

1.4 失效模式优化方法及流程

结构的整体抗震性能由结构的薄弱环节控制，设想结构各构件具有相同的损伤值时，结构不存在薄弱层或薄弱区域，具有最强的抗震性能，与此同时，结构各构件的材料强度得以充分利用，在抗震性能优化的基础上实现最低的建造成本．基于上述等损伤指标的结构优化设计方法的优化目标是减小结构各层各柱构件之间损伤值的差异，进而使结构各构件的抗震性能相当．

图 1为结构优化过程示意，其中图 1(a)为初始结构，经过损伤分析得到初始结构第 m层第 n类柱构件的损伤值 Dmn，图1(b)中以各实心小球的半径分别代表按照上述损伤准则确定的结构各层损伤值的相对大小，根据初始结构的损伤值大小并结合结构在各地震动水平下的损伤程度及不同设防水准下结构评估准则确定如图 1(e)所示的最优结构，其中，以半径为 44的实心小球代表最优结构的目标层损伤值D0，实心小球半径相等代表结构各层损伤水平相当．检测初始结构的约束条件和收敛条件，按照预设步长ΔS1确定初始结构优化指标(截面尺寸、纵筋配筋率等)变化量(图 1(b))，并以此更新优化完毕的结构，结构第m层第n类柱构件优化指标更新为

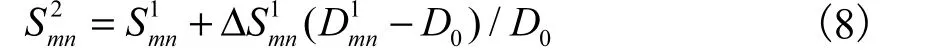
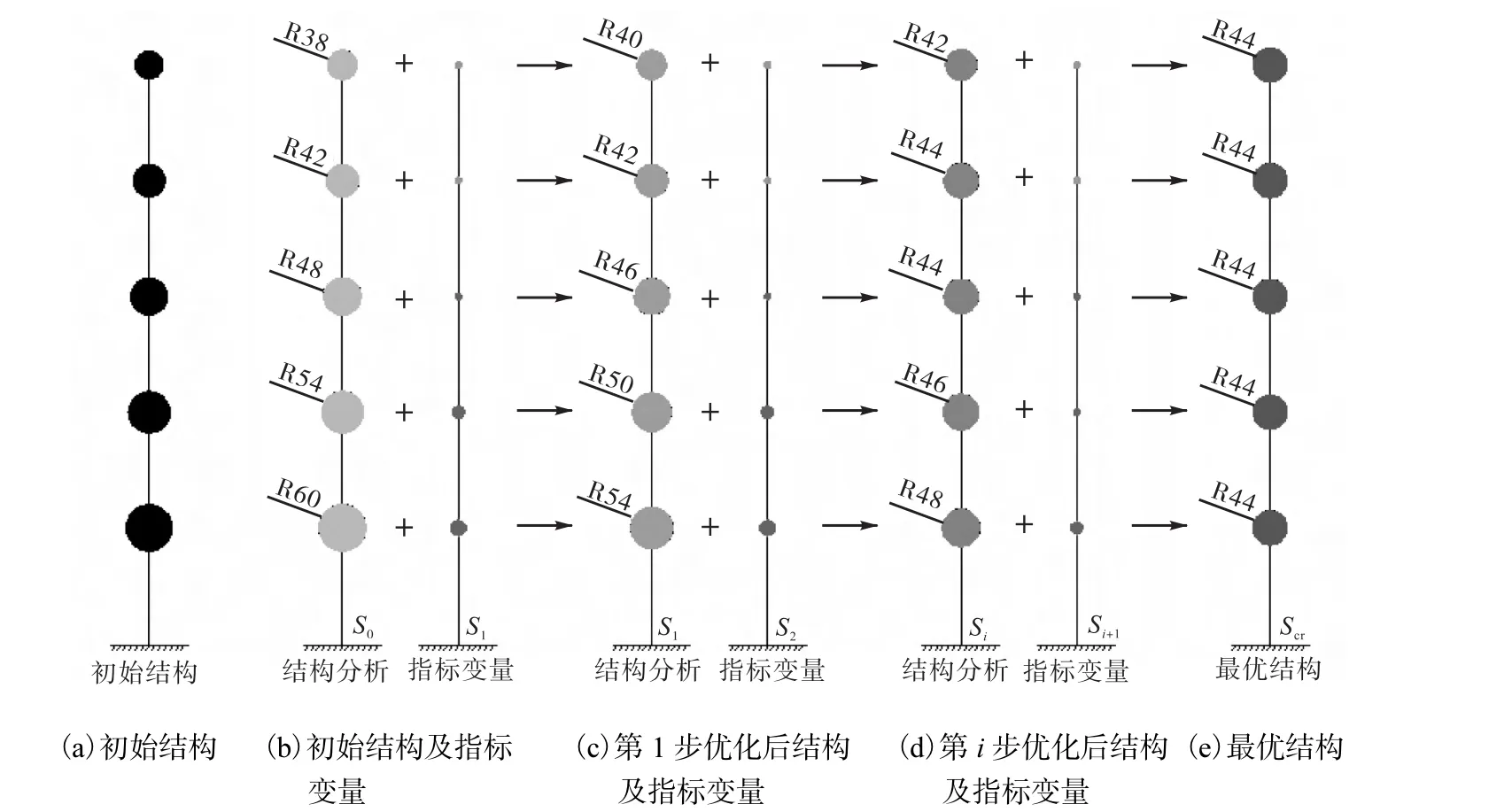
图1 结构优化过程示意Fig.1 Schematic of structure optimization process

分析得到优化后结构各层各类柱的损伤值，图1(c)为1步优化后结构各层的损伤值，经过优化后结构各层的损伤值更趋于最优结构，经过 i步优化后(图 1（d)），最终实现最优结构的损伤水平，其中最优结构第m层第n类柱构件优化指标更新为

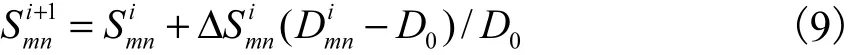
2 数值分析与验证

2.1 Benchmark结构模型

以12层Benchmark钢筋混凝土框架为例，本工程抗震设防烈度为 9度，建筑场地类别为Ⅱ类，结构底层层高 4.6,m，其余各层层高 4.0,m，结构总高度为48.6,m，横纵两向各有 5跨，每跨的跨度为 7.6,m，楼板厚度为 120,mm，框架柱截面自底层向上每 4层改变1次截面，纵筋配筋率分别在第1、5、9层变化；各层梁截面尺寸相同，梁柱截面尺寸、配筋率和配箍率见文献[9]．结构平面及各类柱划分如图2所示．

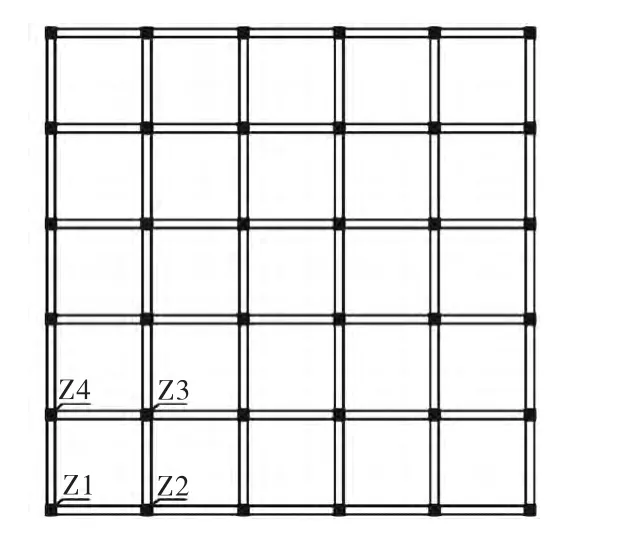
图2 结构底层平面图Fig.2 First floor plan of the structure

利用 ANSYS/LS-DYNA联合建模求解技术，钢筋混凝土框架梁柱均采用 Hughes-Liu非线性显示纤维梁单元模拟，楼板采用分层壳单元模拟，为了更好地体现钢筋混凝土框架结构的动力特性，采用考虑 T型梁效应的楼板与梁协同工作模型[10]，将楼板轴线上移至距离框架梁上表面一半板厚处，并假定楼板平面内刚度无限大；框架柱沿轴向不均匀离散成 11个单元(柱顶及柱底较密)，框架梁沿轴向均匀离散成 5个单元，结构有限元模型如图 3所示．其中，钢筋混凝土框架梁柱采用叠层梁单元法[11]模拟，且纵向钢筋按照面积相等原则进行等效，梁柱混凝土截面均离散为49个纤维，钢筋截面均离散为24个纤维；箍筋的约束效应使核心区混凝土的抗压强度和延性得到显著的提高，假定约束区混凝土与普通混凝土遵循相同的损伤演化法则，则计算核心区混凝土的受压强度和应变[12]公式为

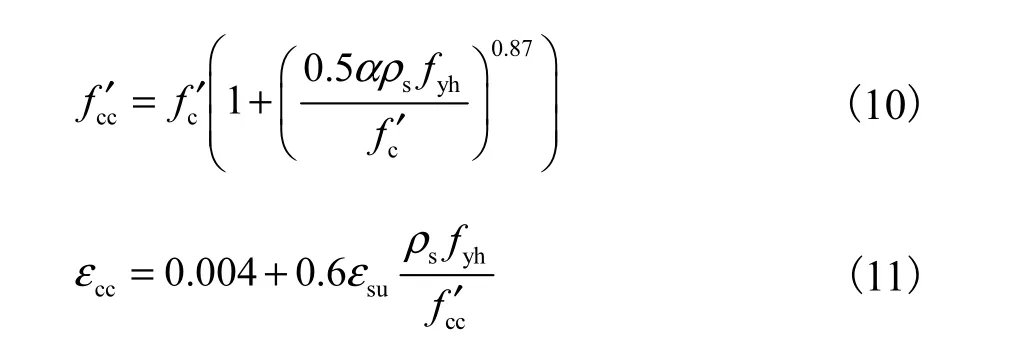
式中：f′cc和 f′c分别为核心区和普通混凝土的抗压强度；ccε和suε分别为相应的应变；yhf为箍筋的屈服强度；sρ为箍筋的体积配箍率；α为箍筋对核心区混凝土的有效约束系数．

图3 结构有限元模型Fig.3 Finite element model of the structure

模型采用刚性地基假定，并沿结构基底输入两个方向水平地震动．图 4所示为柱截面等效纤维单元离散示意．

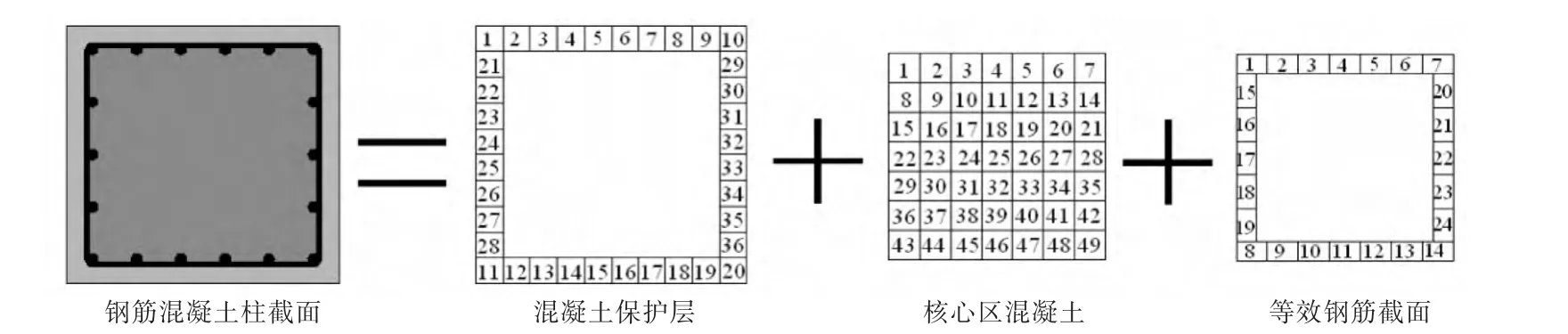
图4 柱截面等效纤维单元离散示意Fig.4 Equivalent fiber unit discrete of the column cross-section

2.2 结构动力响应分析

以峰值加速度(PGA)作为地震动强度指标，强震作用下 PGA调幅至 0.6g，分别对结构基底输入双向的El-Centro、Loma Prieta和Kobe地震动，不同地震动作用下结构各层各类柱的损伤包络线如图 5所示．图中Z1、Z2、Z3和Z4分别代表图2所示结构各层的角柱、边柱与中柱．

由图 5可以看出，结构各层的各类柱在 El-Centro波的作用下具有最大的动力响应，且中柱具有最大的损伤值，边柱次之，角柱最小．这是由于中柱受到的惯性力最大，而角柱最小导致的，结构两边柱损伤值的差异主要是由 x和 y向地震动特性的差异造成的；相同地震动作用下各层各类柱的损伤值有差别，但各层损伤变化趋势类似，结构在 El-Centro波、Loma Prieta波以及Kobe波的作用下均表现为在第9层各类柱的损伤值曲线发生突变，原因是结构在第 9层柱截面由 760,mm×760,mm变成 710,mm×710,mm，形成了薄弱层；而所选3条地震波作用下底层各柱的损伤值几乎都高于其他非薄弱层，说明除第9层之外，底层也是结构的薄弱层．

2.3 失效模式优化分析

由图 5可以看出，由于地震动发生的时间、空间以及峰值、持时等因素的随机性，不同地震动作用下结构各层各类柱的响应不尽相同，为了避免地震动选取的随机性对结构优化的影响，以最不利地震动作为地震激励对结构进行优化．分析表明，在所选的 3条地震波中，El-Centro地震波激励下结构损伤最大．以各层各类柱的损伤值为目标函数，柱构件纵筋配筋率为优化变量，并根据结构构件的安全评估损伤等级指标[13]，优化过程满足所有构件损伤值 D0不大于0.01，由于 Bonora损伤本构模型定义钢材的损伤值达到 0.065时认为其已经破坏，所以，归一化后的钢材损伤值不大于 0.15．考虑结构不同层不同种类柱构件达到目标损伤值的收敛速度有所不同，所有柱构件不可能同时达到目标损伤值，为了避免个别层柱构件的损伤值在目标值附近出现较大浮动，设定结构初始优化的步长为 2,000,mm2，之后每优化步的优化步长均减小为 1,000,mm2，经过 8步优化后，结构构件能够基本满足预设优化条件，达到优化目标．图6所示为El-Centro波作用下结构第1、4、8优化步结构各层各柱构件的损伤包络图．第 8优化步后最优结构的各层柱构件纵筋配筋率如表1所示．

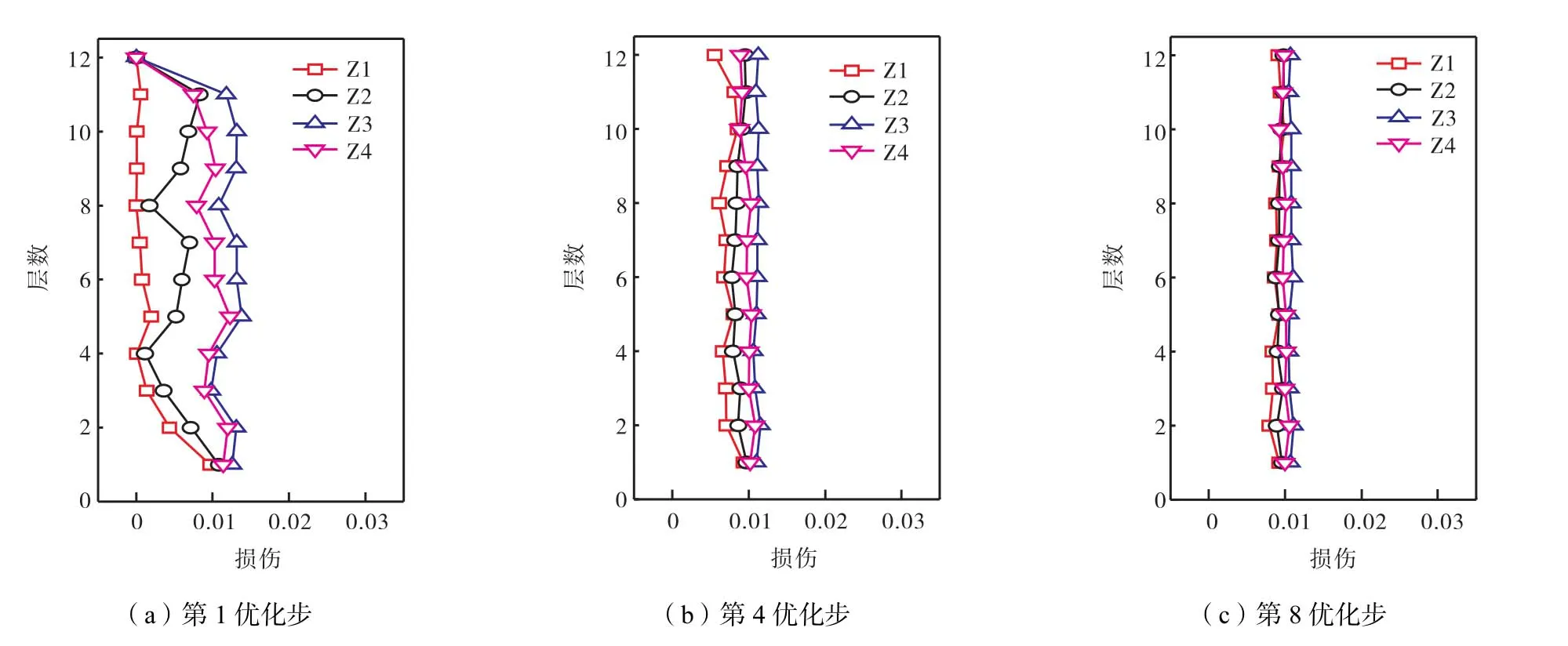
图6 El-Centro波作用下结构各层各柱构件损伤包络线Fig.6 Damage envelope curves for each type of column under El-Centro

表1 最优结构各层柱构件配筋率Tab.1 Reinforcement ratio of the optimal structure %

2.4 优化结果分析

对结构进行层损伤分析，分别得到初始结构和最优结构(第8优化步后的结构)的层损伤发展过程，如图6所示．

由图 5(a)和图 6(a)可以看出，上述优化方法具有很快的收敛速度，经过1次优化后柱构件损伤集中的现象有很大改善，损伤曲线较初始结构更为平缓，结构各层损伤分布更加均匀，但4层以上的角柱几乎没有损伤，各类柱构件损伤值仍然存在较大差异．综合图 6可以看出，优化过程中，各类柱损伤值差异逐渐减小，损伤分布愈加均匀，随着优化步数的增大，结构各层柱向优化目标的收敛速度逐渐减慢，结构底层柱具有最快的收敛速度且在后期的各优化步中有较好的稳定性，经过第 8优化步之后，各层各类柱的损伤值几乎都均匀收敛于预设目标，优化效果明显．

图7 El-Centro波作用下结构各层损伤发展过程Fig.7 Damage development process for each story of the structure under El-Centro

由图 7(a)、(b)可以看出，初始结构各层的损伤发展趋势类似，结构层损伤分别在x向地震动峰值加速度时刻(第2.1秒)、y向地震动峰值加速度时刻(第11.5秒)以及 x向、y向地震动幅值都相对较大时刻(第4.5秒左右)发展较快，损伤曲线出现爬升段，其他时刻损伤值缓慢增加，15,s后损伤值不再发生变化；但是结构各层损伤值差别较大，其中损伤主要集中于首层，而第 12层几乎没有损伤．由图 7(c)、(d)可以

看出，最优结构各层的损伤分布均匀，损伤集中得到了较好的控制．验证了上述以框架结构构件为优化对象的优化方法的可行性及有效性．

通过上述结构整体损伤的定义方法得到初始结构、第2优化步、第4优化步以及最优结构的整体损伤发展，如图8所示．

从图8中可以看到，所采用的优化方法具有很快的收敛速度，经过 2步优化后，结构整体损伤值有大幅减小，随着结构整体损伤接近目标损伤值，其优化收敛速度逐渐下降；最优结构的整体损伤比初始结构有显著的减小，优化并没有改变整体结构的损伤发展趋势，优化后的结构在非地震动峰值时刻损伤发展平稳而缓慢，与最优结构相比，初始结构在非地震动峰值时刻损伤发展相对较快，峰值时刻过后损伤值持续增加，这是由地震作用下初始结构损伤集中于底层使得结构损伤阈值下降导致的．结构整体损伤分析证明上述优化方法能够有效显著地提高结构的抗震性能.

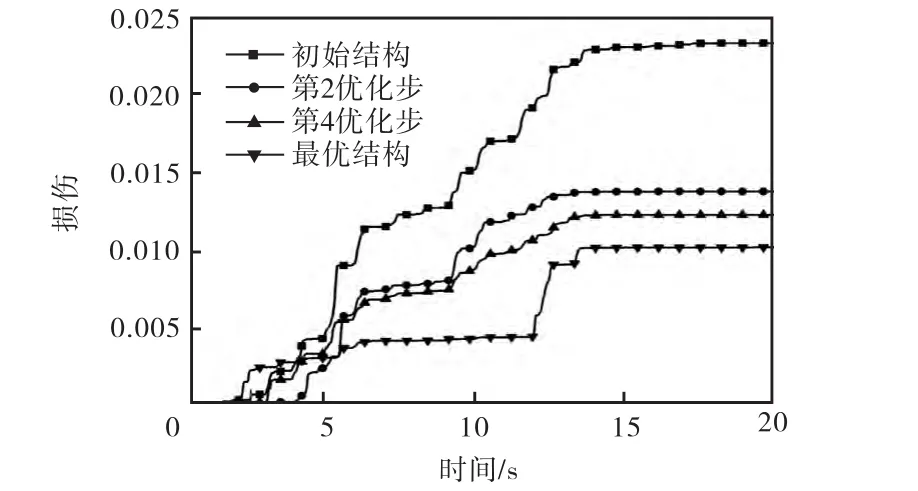
图8 结构整体损伤发展过程Fig.8 Damage development process of the structure

3 结 语

本文采用针对纤维单元模型定义的钢筋混凝土框架结构构件、结构层以及整体结构的损伤准则，以结构构件损伤值相等为目标，对强震作用下的钢筋混凝凝土框架结构的失效模式进行了优化．以 12层的Benchmark钢筋混凝土框架结构为例，对双向 El-Centro地震作用下的结构进行了以柱构件为对象的优化，结果表明最优结构各层各柱构件基本能够满足预设的优化目标；综合结构层以及整体结构的损伤分析结果，所采用的优化方法具有以下优点：能够有效地控制结构层的损伤集中现象，使结构层的损伤沿楼层分布更加均匀，薄弱层的损伤值减小；钢筋混凝土框架结构的抗震性能得到显著的提高．

［1］ Kim J，Seo Y. Seismic design of low-rise steel frames with buckling-restrained braces [J].Engineering Structure，2004，26(5)：543-551.

［2］ Hajirasouliha Iman，Asadi Payam，Pilakoutas Kypros.An efficient performance-based seismic design method for reinforced concrete frames[J].Earthquake Engineering and Structural Dynamic，2012，41(4)：663-679.

［3］ 吕 杨. 高层建筑结构地震失效模式优化及损伤控制研究[D]. 天津：天津大学建筑工程学院，2012.

Lü Yang. Failure Mode Optimization and Damage Control of Tall Building Structures Under Seismic Excitations [D]. Tianjin：School of Civil Engineering，Tianjin University，2012(in Chinese).

［4］ Pirondi A，Bonora N. Simulation of failure under cyclic plastic loading by damage models [J].International Journal of Plasticity，2006，22(11)：2146-2170.

［5］ 李忠献，吕 杨，徐龙河，等. 高层钢框架结构地震失效模式优化及损伤控制研究进展[J]. 建筑结构学报，2011，32(12)：62-70.

Li Zhongxian，Lü Yang，Xu Longhe，et al. Advances in failure mode optimization and damage control for highrise steel frames during earthquake [J].Journal of Building Structures，2011，32(12)：62-70(in Chinese).

［6］ Faria R，Oliver J. ARate Dependent Plastic-Damage Constitutive Model for Large Scale Computations in Concrete Structures[M]. Barcelona，Spain：CIMNE，1993.

［7］ 李 正，李忠献. 一种修正的混凝土弹性损伤本构模型及其应用[J]. 工程力学，2011，28(8)：145-150.

Li Zheng，Li Zhongxian. A modified elastic damage constitutive model of concrete and its applications [J].Engineering Mechanics，2011，28(8)：145-150(in Chinese).

［8］ 吕 杨，徐龙河，李忠献，等. 应用纤维单元模型的钢筋混凝土框架结构损伤与失效分析[J]. 天津大学学报，2011，44(10)：925-929.

Lü Yang，Xu Longhe，Li Zhongxian，et al. Damage and failure analysis of reinforced concrete frame structure using fiber element model [J].Journal of Tianjin University，2011，44(10)：925-929(in Chinese).

［9］ Haselton C B，Goulet C A，Mitrani-Reiser J，et al. An Assessment to Benchmark the Seismic Performance of a Code-Conforming Reinforced Concrete Moment-Frame Building [R]. Berkeley，2008.

［10］ 王洪涛，谢礼立. 考虑楼板作用的钢筋混凝土框架有限元模型及并行计算效率[J]. 地震工程与工程振动，2009，29(1)：63-69.

Wang Hongtao，Xie Lili. Finite element model of RC frame structures and efficiency of parallel computation[J]. Journal of Earthquake Engineering and EngineeringVibration，2009，29(1)：63-69(in Chinese).

［11］ Susantha K A S，Ge H B，Usami T. Cyclic analysis and capacity prediction of concrete-filled steel box columns[J]. Earthquake Engineering and Structural Dynamics，2002，31(2)：195-216.

［12］ Panagiotakos T B，Fardis M N. Deformations of reinforced concrete members at yielding and ultimate [J].Structural Journal，2001，98(2)：135-148.

［13］ 杨佑发，崔 波. 框架结构爆破地震的损伤评估[J].振动与冲击，2009，28(10)：191-194，234.

Yang Youfa，Cui Bo. Damage assessment of a frame structure due to blasting induced ground motions [J].Journal of Vibration and Shock，2009，28(10)：191-194，234(in Chinese).