不同扩散角下汽车风洞试验段轴向静压系数

李启良，陈 力，杨志刚，徐玉冬

（同济大学 上海地面交通工具风洞中心，上海 201804）

汽车风洞是汽车研究与开发的必要测试设施.开口回流式成为现代汽车风洞的主要形式.在汽车风洞设计初期，喷口面积、试验段长度和收集口大小都是重要的设计参数.喷口面积通常由待测车型的最大迎风面积来确定.试验段长度受空间和建设成本的限制尽量做到大于待测车型长度的2倍，这样才能使汽车尾流获得充分的发展，也能提高风洞运行效率.除此之外，它应与收集口的大小紧密结合.试验段轴向静压系数是评价汽车风洞流场品质的重要指标［1］，它受试验段长度、收集口大小和角度的影响.为了优化试验段轴向静压系数分布，研究者基于同济汽车风洞（SAWTC）发现可以通过改变收集口角度和收集口喉部开缝［2］达到效果，对于收集口角度不同风洞表现出不一致的变化规律.SAWTC收集口角度越大，试验段轴向静压系数越小；然而德国斯图加特的汽车风洞（FKFS）收集口角度越大，试验段轴向静压系数越大［3］.

为了明确其中机理，本文建立能够同时考虑试验段长度和收集口大小的变量（扩散角），通过分析不同扩散角下收集口角度与试验段轴向静压系数的变化规律，从而探索预测收集口角度与试验段轴向静压系数变化规律的内在机制.

1 数值模拟方法

立足于模型风洞具体结构和尺寸，选取模型风洞一部分进行模拟，其计算区域包括收缩段、试验段、收集口、扩散段和延伸段，如图1所示.洞壁表面的面网格最小为5mm，最大为20mm.为了更好求解洞壁边界层，在其表面创建边界层网格，使之满足非平衡壁面函数要求［4］.整个计算区域创建四面体网格，网格总数约为530万个.

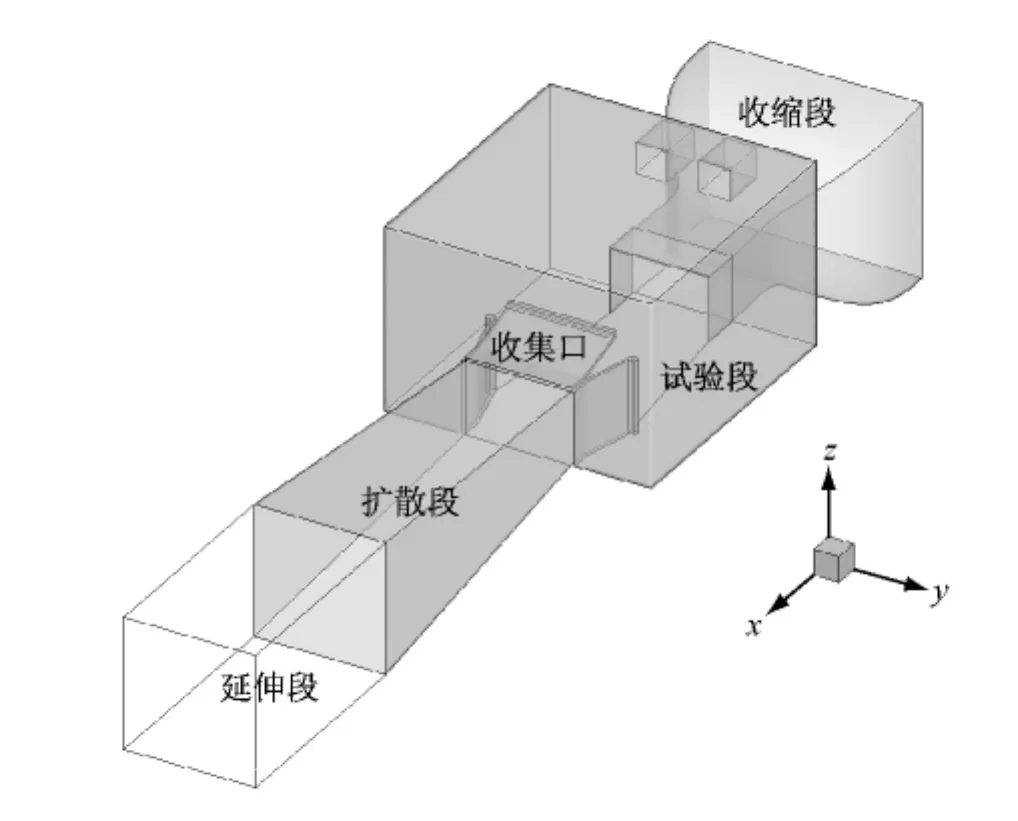
图1 数值模型示意Fig.1 Schematic of numerical model

利用基于有限体积法的商业软件Fluent对非结构网格进行数值求解.湍流场的求解是基于RANS（Reynolds-averaged Navier-Stokes）方程框架中的可实现k-ε（湍动能－耗散率）两方程涡黏性传输模型［5］.无滑移速度边界条件应用于所有洞壁，Fluent软件自带的非平衡壁面函数与可实现k-ε湍流模型用于湍流区域求解.在收缩段进口设定与试验相同的速率（30m·s－1），出口设为自由出流.数值计算首先选用较为稳定的一阶格式，经2 000次迭代后选用精度更高的二阶格式.在满足设定残差和监控物理量为常量后停止初次迭代.根据表征近壁面距离量纲为一的y＋值进行网格加密后继续迭代，直到y＋在30～200之间才停止迭代，因为这个区域被认为是壁面函数的有效区域，另外监控物理量也需保持不变.

为了综合评估收集口大小、角度和试验段长度的关系，引入扩散角，如图2所示.固定喷口尺寸（高为0.283m，宽为0.433m，当量直径为0.342m）和试验段长度，通过改变收集口大小来实现扩散角的变化.表1给出不同扩散角下SAWTC和FKFS风洞的数值模拟尺寸.值得指出的是，FKFS风洞的喷口面积和试验段均比SAWTC小.为了能够将2个风洞统一到相同的喷口大小，对FKFS风洞进行放大，使喷口尺寸与SAWTC风洞相同，此时试验段长度为0.733m.

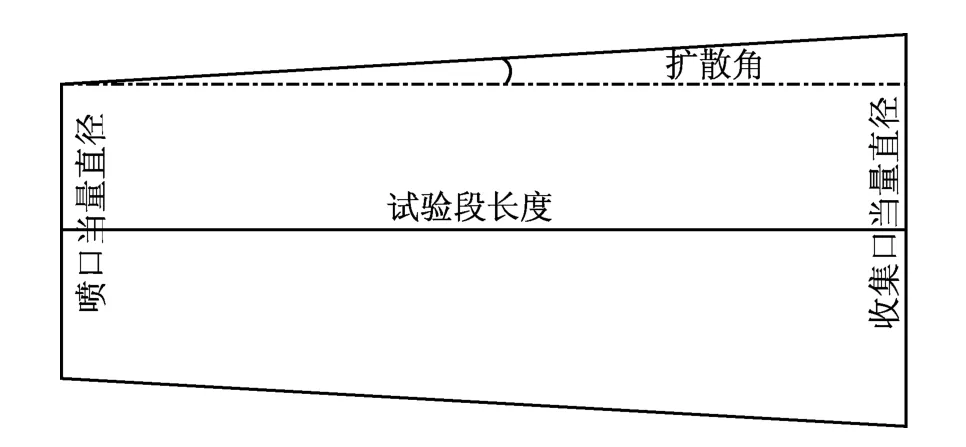
图2 扩散角Fig.2 Diffuser angle

文献［2］讨论了扩散角为3.28°时数值模拟与试验对比，表明所采用的数值模拟方法是正确可行的.不同扩散角工况的计算均按照前面论述的方法来执行.

表1 数值模拟方案Tab.1 Models of numerical simulation

2 结果分析与讨论

选取位于喷口中心对称面且距试验段地面高度为50mm的轴线为参考曲线.在该轴线上以50mm间距创建19个测点，其中以距喷口300mm的测点为参考点.静压系数Cp（x）如式（1）：

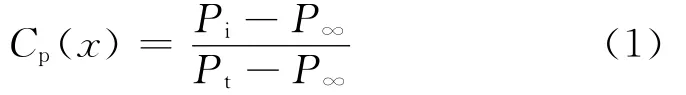
式中：Pi为测点的静压，Pa；P∞为参考点的静压，Pa；Pt为参考点的总压，Pa.

2.1 轴向静压系数变化规律

为了研究扩散角对试验段轴向静压系数的影响，数值模拟了SAWTC风洞和FKFS风洞在不同扩散角下试验段的轴向静压系数分布，如图3所示.从图中可以看出，当扩散角为1.38°时，SAWTC在收集口为0°的最大静压系数为0.024，而FKFS的最大静压系数为0.111.当收集口角度为15°时，SAWTC风洞和FKFS风洞的最大静压系数分别为0.040和0.138.观察扩散角为1.38°时，均能发现收集口角度为0°的静压系数比收集口角度为15°时小.上述变化规律存在于所研究的2个风洞中.扩散角为1.70°时，最大静压系数的变化规律发生改变.对于SAWTC和FKFS风洞，收集口角度为0°和15°均对应着相同的静压系数，当扩散角大于1.70°时，均能发现收集口角度为15°对应的静压系数大于收集口角度为0°时的静压系数.

图3 不同扩散角下轴向静压系数的数值结果Fig.3 Numerical results of axial static pressure at different diffuser angles

目前实际运行的SAWTC风洞的扩散角为3.28°（大于1.70°）时，试验段轴向静压系数随着收集口角度增大而减小.FKFS风洞的扩散角为1.23°（小于1.70°）时，试验段轴向静压系数随着收集口角度增大而增大.在汽车风洞设计时，如果轴向静压系数和低频颤振同等重要，那么需要将扩散角确定在大于1.70°.因为以往研究表明，可以通过增加收集口角度来降低轴向静压系数和低频颤振脉动系数［6］.否则，有可能存在两者必须取舍的状况.

2.2 机理分析

2.2.1 动压与总压

为了了解其内在机理，图4给出了不同扩散角下测点动压和总压变化曲线.从图中可以看出，测点的总压几乎不随扩散角的变化而变化，基本为定值.随着测点位置从－0.3至0.5变化，测点动压先缓慢增加后快速减少.这主要是因为靠近喷口处，当地静压小于环境压力，气流在压差作用下进入射流区，随着气流逐渐靠近收集口，由于收集口面积加大，扩散作用较明显，气流流速快速下降.

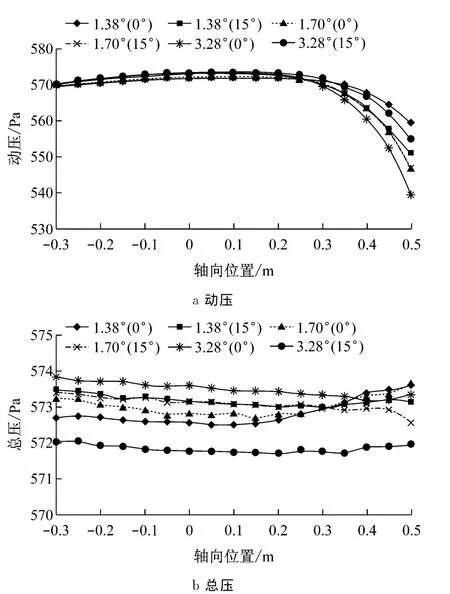
图4 不同扩散角下动压与总压的变化Fig.4 Dynamic and total pressures at different diffuser angles

当扩散角为1.38°时，收集口角度为0°对应的测点动压大于收集口角度为15°时的动压.当扩散角为1.70°时，两者的动压几乎相等.当扩散角大于1.70°时，收集口角度为0°对应的测点动压小于收集口角度为15°时的动压.收集口角度的变大将使流动扩散作用更强和外界更多气流进入到流动的轴向区域.前者使动压下降，后者将使动压上升.显然，在扩散角为1.70°时，两者达到平衡.而扩散角小于1.70°时，前者的作用更强；扩散角大于1.70°时，后者作用更强.

2.2.2 耗散率

开口式风洞存在典型的射流剪切层.为了更加形象给出射流剪切层的结构，图5给出了扩散角为1.70°时离地高度为50mm的水平截面的耗散率.从图中可以清楚看出，左右两侧存在明显的剪切层结构.在剪切层中，涡流运动激烈，湍流耗散较强，它远高于射流核心区.与此同时，剪切层在向下游运动过程中以一定的角度发展和扩散，该角度约为1.70°.这与上述角度一致.由此可知，导致轴向静压系数在扩散角为1.70°出现分界线的根本原因来自于射流剪切层自身的扩散.由于射流剪切层耗散角度不随收集口的变化而变化，因此当收集口较大且由此导致扩散角大于射流耗散角时，收集口角度越大，外界气流进入轴向流动区域越多，它超越角度变大带来的效应而导致动压的增加.与之相反的是，当收集口较小且由此导致扩散角小于射流耗散角时，收集口角度增加带来的效应更加明显，表现出动压的相对减少.

图5 扩散角为1.70°时射流剪切层的耗散云图Fig.5 Dissipation contour of shear layer at diffuser angle of 1.70°

3 结论

建立能够表征收集口大小和试验段长度的物理量（扩散角），研究SAWTC风洞和FKFS风洞在不同扩散角下试验段轴向静压系数变化规律.

当扩散角大于1.70°时，收集口角度越大，试验段轴向静压系数越小.当扩散角等于1.70°时，试验段轴向静压系数不随收集口角度的变化而变化.当扩散角小于1.70°时，收集口角度越大，试验段轴向静压系数越大.

射流剪切层的耗散角是揭示试验段轴向静压系数变化规律的根本.当扩散角等于耗散角时，收集口角度变化带来的扩散效应与外界气流进入流动轴向区域效应相同，表现出静压和动压不随收集口角度变化而变化.当扩散角小于耗散角时，收集口角度变化带来的扩散效应更强，反之，则更弱.

应该指出的是，上述规律应用于所有存在收集口的开口式风洞中.

［1］ 中国人民解放军总装备部军事训练教材编辑工作委员会.高低速风洞气动与结构设计［M］.北京：国防工业出版社，2003.

Editorial Committee of Military Training Book of General Armament Department of the Chinese People’s Liberation Army.Aerodynamic and structure design of high and low speed wind tunnel［M］.Beijing：National Defense Industry Press，2003.

［2］ 李启良，郑志强，贾青，等.两种改善汽车风洞轴向静压系数的方法［J］.同济大学学报：自然科学版，2010，38（3）：422.

LI Qiliang，ZHENG Zhiqiang，JIA Qing，etal.Numerical and experimental study on two methods to improve the axial static pressure coefficient of automotive wind tunnel［J］.Journal of Tongji University：Natural Science，2010，38（3）：422.

［3］ Künstner R，Potthoff J，Essers U.The aero-acoustic wind tunnel of Stuttgart university［C］／／Social Automotive Engineering.［S.L.］：SAE，1995：950625.

［4］ Launder B E，Spalding D B.The numerical computation of turbulent flows［J］. Computational Methods in Applied Mechanics and Engineering，1974，3（2）：269.

［5］ Shih T H，Liou W W，Shabbir A，etal.A newk-εeddy viscosity model for high Reynolds number turbulent flows：model development and validation［J］.Computers and Fluids.1995，24（3）：227.

［6］ 郑志强.汽车气动声学风洞低频颤振现象研究及控制［D］.上海：同济大学，2009.

ZHENG Zhiqiang.Study and control of buffeting phenomenon for automotive aero-acoustic wind tunnel［D］.Shanghai：Tongji University，2009.