不同全球对流层天顶延迟产品在中国区域的比较

李博峰，王苗苗，沈云中，楼立志

（同济大学 测绘与地理信息学院，上海 200092）

电离层与对流层误差是GNSS（Global Navigation Satellite System）应用的两大主要误差源，电离层误差可采用多频信号有效消除.尽管对流层误差较电离层小，但在精密定位中无法通过多频信号消除.对流层延迟包括干延迟和湿延迟两部分，其中干延迟约占总延迟的90%，可采用Saastamoinen，Hopfield，UNB3等经验模型进行精确改正［1］.由水汽引起的湿延迟虽然较小，但其变化率是干延迟的3～4倍，因此对流层延迟是制约未来多频多模GNSS模糊度固定、精密定位的主要因素［2－3］.

随着对地观测网络的完善和观测数据的增加，对流层延迟从依赖简单封闭的数学模型向依赖大量外部数据的改正模型过渡［4］.目前已有诸多机构提供全球对流层天顶延迟产品，这些产品采用的数据源、投影函数不同，因此它们的精度和适用区域都不尽相同.IGS（International GNSS Service）融合多个分析中心的结果发布全球对流层天顶延迟产品，其精度可达4mm，应用范围较广［5］.维也纳科技大学UTV（Vienna University of Technology）基于欧洲中尺度气象预报中心的数值气象资料ECMWF-NWM结合 Marini［6］投影函数发布了全球对流层天顶延迟产品，精度可达到2cm，其在欧洲的适用性较好.加拿大新布伦斯威克大学UNB（University of New Brunswick）基于美国国家环境中心和全球多尺度环境中心NCEP-GEM再分析资料结合VMF1［7］投影函数发布了全球对流层天顶延迟产品，其在北美区域的适用性较好.

不同产品采用不同的数据源，即使采用相同的投影函数计算对流层天顶延迟，全球不同区域其精度亦有差异.况且现有产品采用的数据源和投影函数都不尽相同，尽管在各自的数据源区域能取得良好的效果，但是鲜有研究分析这些产品在中国区域内的精度差异.本文分析4种对流层天顶延迟产品及不同对流层高程归算方法和格网插值方法在中国区域内的精度.

1 对流层天顶延迟产品

1.1 VMF1产品

VMF1（Vienna Mapping Functions）格网产品将地球按照地心经度、纬度等间隔地分成2.5°×2.0°的格网，每隔6h提供全球对流层天顶延迟格网产品，数据包括映射函数系数、天顶干延迟（zenith hydrostatic delay，ZHD）和天顶湿延迟（zenith wet delay，ZWD）.除了格网产品，同时还提供全球IGS站点的天顶延迟数据，包括映射函数系数、ZHD和ZWD以及站点气象数据，其时间分辨率与格网产品相同.

图1 UNBVMFG，UNBVMFGcmc和UNBVMFP与VMF1的ZTD差异分布Fig.1 Comparison of ZTD from UNBVMFG，UNBVMFGcmc and UNBVMFP with VMF1

VMF1产品精度较高，可达到2cm，可用于精密的静态定位或者亚米级的定位.通过插值计算，格网对流层天顶延迟能够获得所有站点的天顶对流层延迟，因而比站点对流层延迟产品的应用范围更广泛.

1.2 UNB产品

作为对VMF1产品的一个很好的补充，UNB提供3种全球对流层天顶延迟格网产品，即UNBVMFG， UNBVMFGcmc 和 UNBVMFP.UNBVMFG是利用NCEP-GEM再分析资料得出的产品；UNBVMFGcmc是利用全球确定性预报系统GDPS（Global Deterministic Prediction System）分析得出的产品，其6h和18h的数据以经过6h的预测值为基础；UNBVMFP是利用GDPS分析得出的预测产品，分别预测24，30，36，42h的对流层延迟值.3种产品的延迟分别为7d，1d和0d.图1分别是3种UNB产品与VMF1产品在2012年6月1日12时的全球ZTD（zenith troposphere delay）差异分布图.

3种UNB产品与VMF1产品在2012年6月1日12时的全球差异最小值分别为－174.8，－121.0，－133.2mm，最大值分别为191.9，140.5，164.9mm，平均值分别为7.21，7.56，9.69mm.在中国范围内大部分区域的差异值基本一致，约为20 mm，个别地区出现50mm以上的差异，说明各对流层天顶延迟产品在中国区域内的差异性不尽相同，且在区域上呈现不连续性分布.

2 对流层天顶延迟

2.1 对流层延迟高程改正

格网点ZHD，ZWD参考地形格网点高度hg，站点高度为hs，首先需要将对流层延迟从格网高程归算至站点高程，ZHD的高程归算方法一般有2种.第1种方法较为简单，只考虑对流层随高程变化的物理机制（记为 HGT-CORR改正方法）［8］，即

式中：DH（hs），DH（hg）分别为站点和格网点的干延迟；hg，hs分别为格网点高度和站点高度，m；T（hg）为格网点对应的温度，K；P（hg）为格网点对应的气压，hPa，温度和气压可以由GPT（Global Pressure and Temperature）［9］模型或者标准大气解算；R为气体常数，R＝0.289 644KJ·kg－1；g为重力常数，g＝9.784m·s－2.

另一种ZHD高程归算方法顾及气压的影响（记为PRESS-CORR改正方法），数学公式如下：

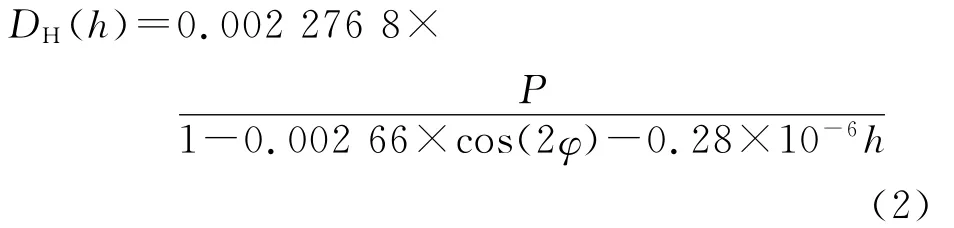
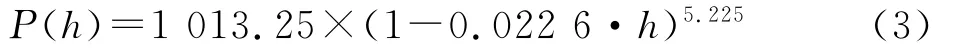
式中：P为气压，hPa；φ为纬度；h为高度，m；已知DH（hg），hg，hs和φ，首先根据式（3）分别计算气压值P（hs），P（hg），再根据已知DH（hg），φ，hg用式（2）反算格网点气压P′（hg），然后计算站点的气压修正值P′（hs）＝P（hs）＋P′（hg）－P（hg），最后将P′（hs）代入式（2）计算站点干延迟DH（hs）［10］.

由水汽引起的湿延迟ZWD变化率大、随机性较强，为了完整性和便于直接比较，类似于干延迟在高程上的改正，选择指数衰减函数对ZWD在高程上进行改正［10］.

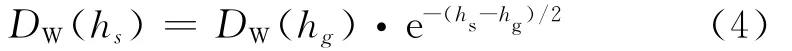
式中，DW（hg），DW（hs）分别是格网点和站点的天顶湿延迟.

2.2 对流层延迟格网插值

格网插值常采用插值方法简单、以格网值近似地遵守线性变化为基础的双线性内插法（BIL）.如图2a所示，设

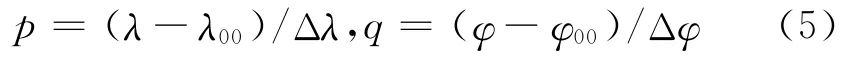
式中：0≤p＜1，0≤q＜1；λ和φ分别为插值点所在的经度和纬度；λ00和φ00分别是插值点所在格网左下角点的经度和纬度.可以先线性内插出点A，B或者点C，D，然后再线性内插出点P.点P的Z（λ，φ）值计算公式为

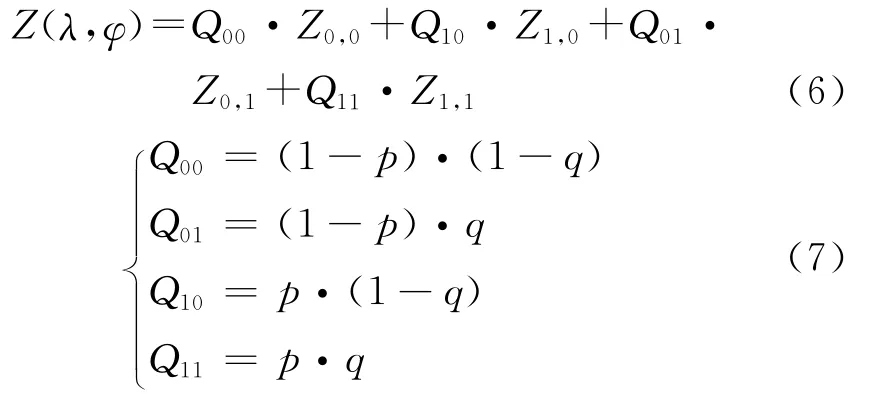
式中：Z0，0，Z1，0，Z0，1，Z1，1分别是点P所在格网各角点的值；Q00，Q10，Q01，Q11分别是对应的因子.

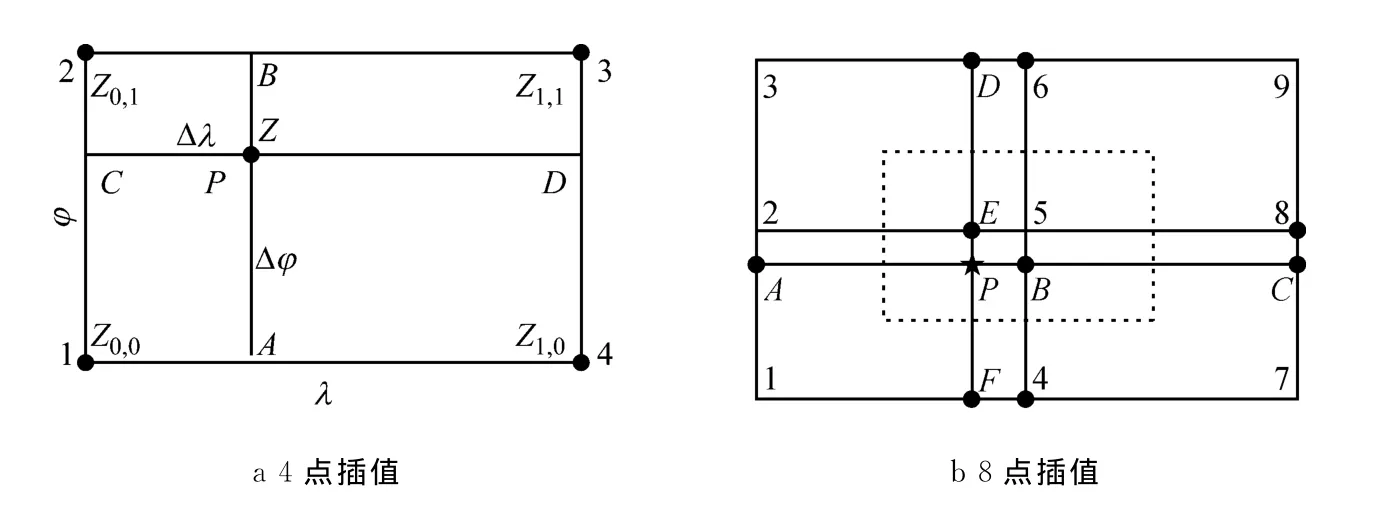
图2 周围4点与8点插值Fig.2 Interpolation with nearby 4points and 8points

另一种常用的计算点P的Z（λ，φ）值的方法为 距离加权格网插值（WGI）［11］.不同于BIL方法，定义函数Q（p，q）为

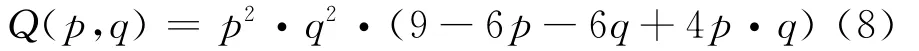
则Q00，Q10，Q01，Q11分别为

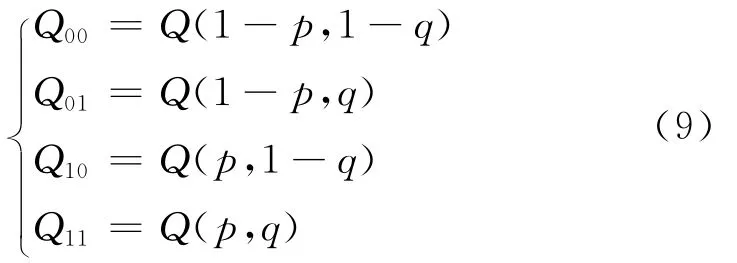
还可采用双二次多项式内插方法（BIQ），其对由单个格网拼接成整体曲面造成的不光滑以及格网点处形成“尖点”和格网边上形成“折痕”有所改善［12］.设平面上3点满足二次多项式y＝ax2＋bx＋c，由3个已知点计算出多项式系数，从而可计算出任意点的对流层延迟.如图2b所示，找到与插值点P距离最近的中心格网点（图中点5），用中心点周围的点1～9对点P进行插值.由点1～3插值点A，点4～6插值点B，点7～9插值点C，然后由A，B，C三点插值计算点P.

3 试验分析

综合格网插值方法和干延迟在高程上的归算方法，组成计算方案1～6如下：BIL与HGT-CORR组合；BIL 与 PRESS-CORR 组 合；WGI与 HGTCORR组合；WGI与PRESS-CORR组合；BIQ与HGT-CORR组合；BIQ与PRESS-CORR组合.

各方案采用的湿延迟改正方式相同.采用中国区域内9个IGS站从2012年6月1日至9月1日共92d的数据，用6种计算方案计算比较4种全球对流层天顶延迟格网产品和干延迟高程归算方法及格网插值方法在中国不同区域的差异性.试验中，内插站点的ZTD以IGS提供的产品值为参考，ZHD，ZWD分别以VMF1站点产品的ZHD，ZWD为参考.表1是9个IGS站点的基本信息.

表中各站点的高程离散度Δh按式（10）计算：

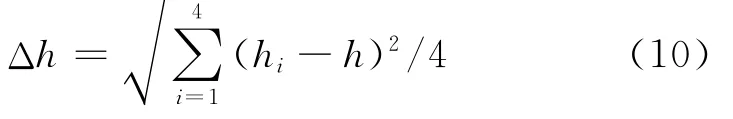
式中：hi为站点所在格网第i个格网点的高程；h为站点的高程.站点高程离散度用于反映内插站点高程相对于格网点高程的相对变化幅度.

首先分析VMF1对流层格网产品.对VMF1对流层格网产品分别采用6种方案计算9个IGS站92 d的ZTD，然后分别统计它们的内符合精度（STD）和外符合精度（RMS），如图3所示.除此之外，还分析了不同方案ZHD和ZWD的内插效果，其统计结果如表2，其中方案1，3，5的RMS统计不包括LHAZ站.

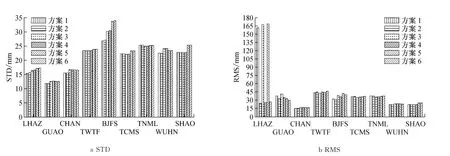
图3 VMF1产品的内符合精度与外符合精度Fig.3 STD and RMS of ZTD from VMF1

除了拉萨站LHAZ外，各站点6种方案获得的ZTD，ZHD和ZWD的精度基本一致，外符合精度分别小于50，20，40mm；方案间相差最大分别不超过10，5，8mm；所有站点平均偏差值均分别在－40～30mm，－15～20mm，－20～25mm之间；所有站点的内符合精度均分别小于35.0，3.2，32.0mm，即对流层延迟在高程上的归算方法和插值方法在站点上差异不明显.相同的方案在不同的区域计算的精度有差异，外符合精度差异最大分别约为30，16，30 mm，说明不同的区域影响对流层延迟在高程上的归算方法和插值方法的精度.站点内符合精度之间的差异说明产品在不同区域的稳定性不同.

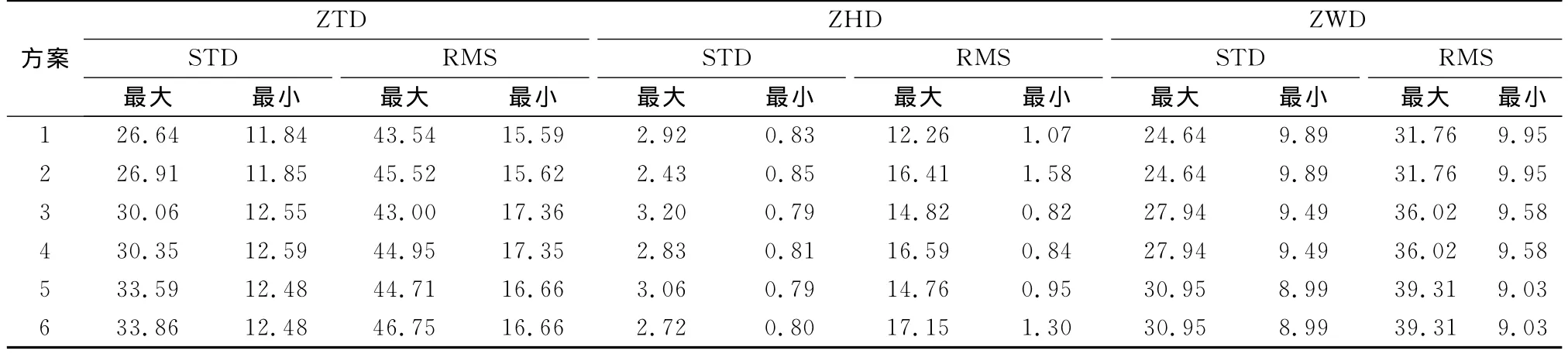
表2 6种方案计算的内外符合精度统计Tab.2 STD and RMS from six interpolation schemes mm

对流层天顶干延迟的归算精度与内插点的高程离散度相关，对LHAZ站而言，其高程离散度为1 614.57m，远大于其他IGS站，所以干延迟高程归算方法在LHAZ产生约145mm的精度差异，而在其他站点差异不明显.因此，LHAZ站较大的高程离散度是导致2种干延迟高程归算方法（HGT-CORR和PRESS-CORR）产生较大差异的原因，并且HGT-CORR方法对高程离散度更为敏感，在高程离散度较大时，改正精度较低；而PRESS-CORR方法能有效克服HGT-CORR的缺陷，即使对高程离散度较大的LHAZ站也能取得较好效果.当高程离散度较小时，2种干延迟高程归算方法都能取得良好的效果.

类似于对VMF1产品的分析，对3种UNB对流层产品也做了分析，得到类似的结论.

由上述分析知，6种方案在各站点获得的对流层延迟精度基本一致，现选择方案4分析4种对流层产品.采用方案4分别计算4种格网产品获得各站点的对流层延迟，统计其内外符合精度，其中ZTD的内外符合精度如图4，对应的统计结果如表3.

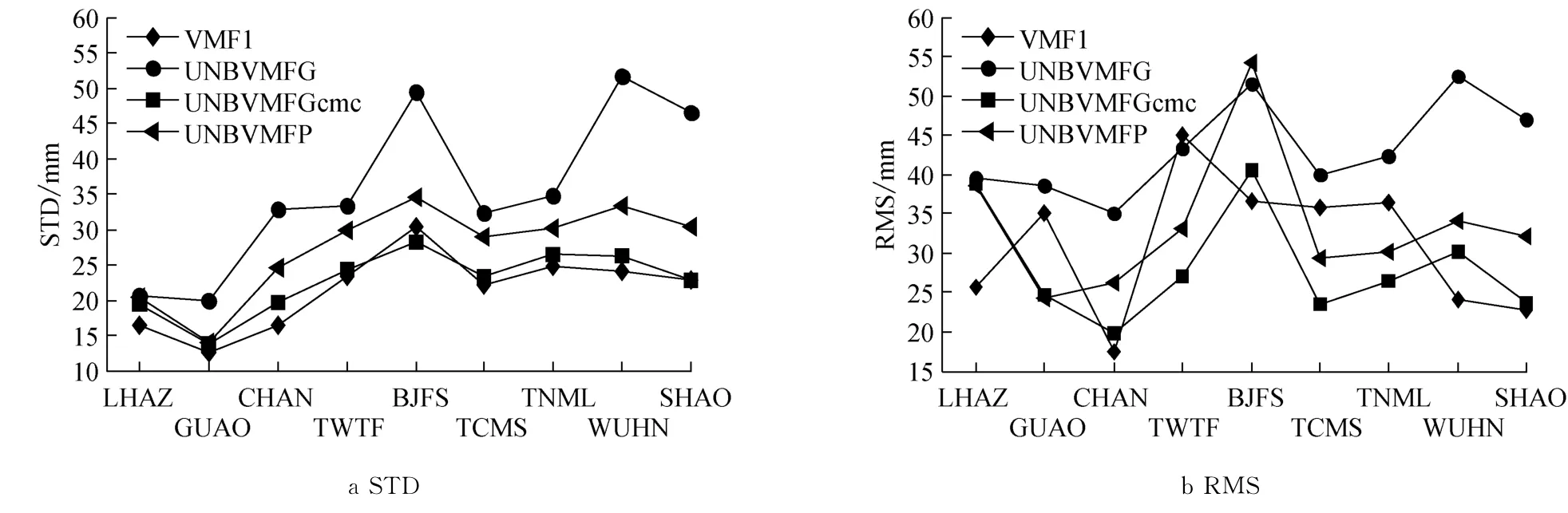
图4 4种产品计算ZTD的内符合精度和外符合精度Fig.4 STD and RMS of ZTD from four different products

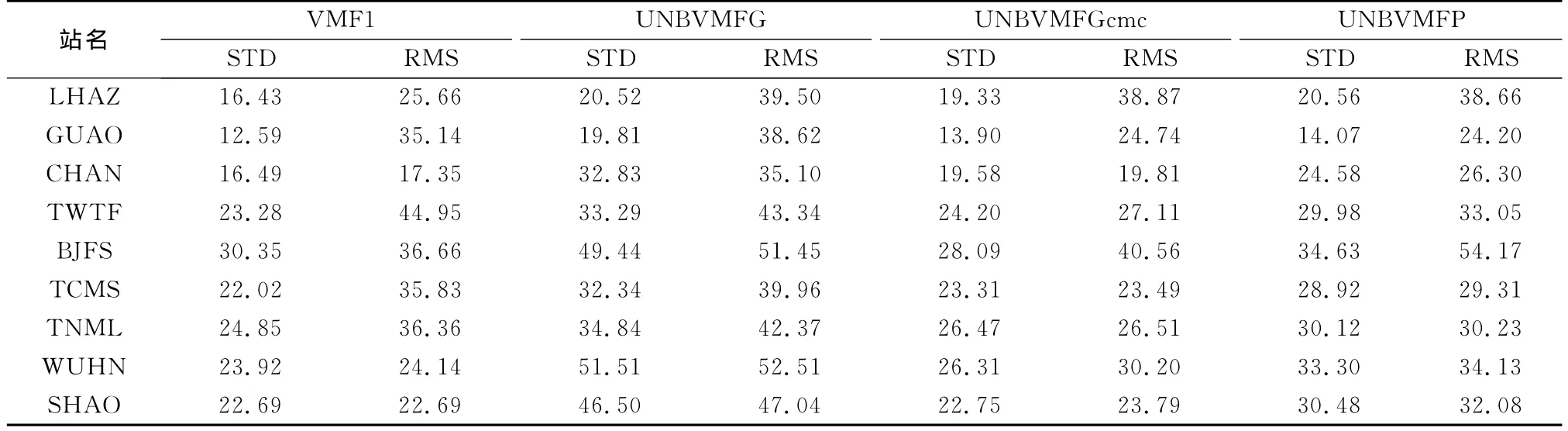
表3 4种产品计算的ZTD的内符合精度与外符合精度Tab.3 STD and RMS of ZTD from four different products mm

采用方案4计算UNB提供的3种对流层天顶延迟产品获得的ZTD，ZHD和ZWD的精度在区域上的变化基本一致，差值最大分别约为25，3，25mm，UNBVMFG产品在中国区域精度相对较低（除BJFS站外），而UNBVMFGcmc产品在中国区域的精度相对较高.在GUAO，BJFS，WUHN站处，VMF1产品与3种UNB产品在区域上的变化有差异，并且各产品在区域上的精度变化也有不同.分析原因可能是由于2个机构提供的对流层天顶延迟产品采用的数据源、映射函数和计算方法不同引起产品的精度变化在区域上呈现差异性.

4种对流层天顶延迟产品获得的站点ZTD，ZHD和ZWD的内符合精度STD在区域上的变化基本一致（UNBVMFG在区域上的变化幅度稍大），差值最大分别约为25，3，30mm.UNBVMFG产品在中国区域的稳定性相对较差，VMF1产品的稳定性相对较高.

4 结论

选取中国区域内9个IGS站点，采用6种方案分析了4种全球对流层天顶延迟格网产品VMF1，UNBVMFG，UNBVMFGcmc，UNBVMFP，分析结果表明，当内插点的高程离散度较大时，单纯以修正高程归算对流层干延迟的方式对高程离散度更加敏感，高程离散度大时获得的精度较低，而气压修正的方式可以克服该缺陷.区域差异影响对流层延迟在高程上的归算方法和插值方法的精度.各产品在中国区域内的精度和稳定性及其在区域上的变化不尽相同，但是各产品都可以灵活地为导航、定位、水汽反演等应用提供一定精度的对流层天顶延迟.

［1］ 杨玲，李博峰，楼立志.不同对流层模型对GPS定位结果的影响［J］.测绘通报，2009，4（3）：9.

YANG Ling，LI Bofeng，LOU Lizhi.Effects of different troposphere correction models on GPS positioning［J］.Bulletin of Surveying and Mapping，2009，4（3）：9.

［2］ 李博峰.混合整数GPS线性模型的参数与方差－协方差分量估计理论与方法［D］.上海：同济大学，2010.

LI Bofeng.Theory and method for parameter and variancecovariance component estimation in mixed integer linear GPS model［D］.Shanghai：Tongji University，2010.

［3］ LI Bofeng，FENG Yanming，SHEN Yunzhong，etal.Geometry-specified troposphere decorrelation for subcentimeter real-time kinematic solutions over long baselines［J］.Journal of Geophysical Research，2010：DOI：10.1029／2010JB007549.

［4］ Urquhart L，Santos M.Development of a VMF1-like service at UNB［D］：Fredericton：Department of Geodesy and Geomatics Engineering of University of New Brunswick，2011.

［5］ Byun S H，Bar-Sever Y E.A new type of troposphere zenith path delay product of the international GNSS service［J］.Journal of Geodesy，2009，83（314）：1.

［6］ Marini J.Correction of satellite tracking data for an arbitrary tropospheric profile［J］.Radio Science，1972，7（2）：223.

［7］ Boehm J，Werl B，Schuh H.Troposphere mapping functions for GPS and very long baseline interferometry from European Centre for medium-range weather forecasts operational analysis data［J］.Journal of Geophysical Research，2006：DOI：10.1029／2005JB003629.

［8］ Steigenberger P，Boehm J，Tesmer V.Comparison of GMF／GPT with VMF1／ECMWF and implications for atmospheric loading［J］.Journal of Geodesy，2009，83（10）：943.

［9］ Boehm J，Heinkelmann R，Schuh H.Short note：aglobal model of pressure and temperature for geodetic applications［J］.Journal of Geodesy，2007，81（10）：679.

［10］ Kouba J.Implementation and testing of the gridded Vienna Mapping Function 1（VMF 1）［J］.Journal of Geodesy，2008，82（4）：193.

［11］ Chao YC. Real Time Implemental of the wide area augumention system for the Global Position System with an emphasis on ionospheric modeling［D］.Stanford：Stanford University，1997.

［12］ 邓兴升，郭云开，花向红.似大地水准面格网双二次多项式插值方法［J］.测绘学报，2009，38（1）：35.

DENG Xingsheng， GUO Yunkai， HUA Xianghong.Quasigeoid grid network bi-quadratic interpolation method［J］.ActaGeodaeticaetCartographicaSinica，2009，38（1）：35.