某型发动机涡轮盘温度及应力计算分析

李 钊，邹 武

（海军装备部，陕西 西安 710021）

0 引言

由于发动机涡轮盘处于高温、高转速的工作状态，承受着由涡轮叶片的离心力和轮盘本身的离心力产生的离心应力、由温度梯度产生的热应力及相关零件变形不协调所引起的附加应力等，且上述应力均随发动机的工作状态改变而变化，因此涡轮盘工作过程中存在着大量的低循环。据统计，航空发动机结构故障占总故障的60%～70%，而疲劳破坏又占发动机结构故障的80%～90%，所以对涡轮盘低循环疲劳寿命进行研究是十分必要的［1］。

涡轮盘低循环疲劳寿命通常是在循环旋转试验器上进行疲劳试验确定的，而在进行低循环疲劳试验前首先要确定涡轮盘的考核部位和试验温度，由于涡轮盘真实的工作应力和温度无法直接测量，采取有限元计算便是一条行之有效的方法［2，3］。

本文利用Patran／Nastran软件建立某型发动机涡轮盘的有限元模型，参考相关文献确定涡轮盘温度场、应力场分析的边界条件，并对温度场和应力场进行计算分析，根据计算结果确定涡轮盘低循环疲劳试验的考核部位。

1 涡轮盘模型的建立

某型发动机高压二级涡轮盘由高温合金GH901锻造并经过机械加工而成，涡轮盘在结构上呈现旋转周期性，即绕其转轴转动α＝2π／N（N为叶片数）角度后，结构的几何形状和转动前完全一样。为计算盘的离心力和热应力，根据圣维南原理，可以先将盘的模型简化，忽略榫槽和前端面安装边上的销孔，简化后涡轮盘的模型在Patran中建立，取1／5的扇形对称体进行三维有限元计算。高压二级涡轮盘的模型如图1所示。

图1 高压二级涡轮盘模型（1／5）

涡轮盘的有限元网格采用六面体八节点单元，在一侧对称面上划分好四边形网格，然后绕Z轴旋转72°，最后将六面体网格与1／5高压二级涡轮盘模型连接即可。

2 高压二级涡轮盘的温度分析

高压二级涡轮盘的热交换主要有涡轮叶片的榫头与轮盘榫槽的传导换热、高压冷却气体与盘身前后端面的对流换热、涡轮盘内孔与定心衬套的传导换热。

对于发动机涡轮部件的温度场分析，在只有部件关键点温度值而缺乏其他数据的情况下，目前多采用一维插值的方法获得涡轮部件的温度场分布［4，5］。本文根据该型发动机性能计算程序中计算出的各性能参数间的关系式对涡轮盘轮缘和内孔温度进行估算，然后在Nastran中计算稳态温度场。

稳态温度计算公式为：

其中：Tb为轮盘内孔总温；Tr为轮盘轮缘总温；Thp2l为高压二级涡轮进口燃气总温；T3为高压压气机出口总温。在发动机最大工作状态下，排气温度T6为961.9 K，涡轮前温度T4＝1 440 K，根据各温度参数间的关系，可以得到：

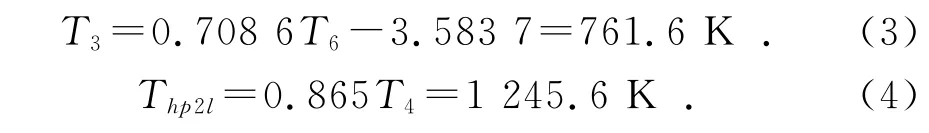
将T3和Thp2l代入式（1）、式（2）得到：Tb＝766.93 K，Tr＝843.95 K。

将上述边界条件输入Nastran中进行计算，得到高压二级涡轮盘在设计状态下的温度场。涡轮盘工作时轮缘温度最高，内孔温度最低，盘身温度从内孔到轮缘逐渐升高；涡轮盘工作的平均温度为805.2 K，盘整体温度分布比较均匀。

3 高压二级涡轮盘应力分析

在发动机工作过程中，涡轮盘主要承受离心载荷、温度载荷、气动载荷、振动载荷等，其中气动载荷、振动载荷对轮盘的静强度影响较小，载荷数据也比较有限，所以本文在进行强度计算时只考虑离心载荷和温度载荷。

3.1 涡轮盘的边界条件确定

（1）力边界条件：假定叶片的离心载荷均匀分布于轮盘榫槽的接触表面上，离心力由一个叶片的质量产生，根据轮缘外表面积计算出离心压力为119.79 MPa；轮盘自身的离心力边界条件为施加一个绕旋转轴的转速。

（2）位移边界条件：由于取1／5盘进行计算，故而约束住1／5轮盘对称面的周向位移；同时将轮盘与轴、轮盘与定位螺母和隔圈的接触问题简化，设置轮盘前、后端面上的轴向位移和内孔的径向位移为0。

（3）温度边界条件：将温度场计算结果定义为一个场，作为轮盘的温度边界条件。

3.2 高压二级涡轮盘有限元计算分析

发动机在最大工作状态下，高压涡轮盘的转速NH＝12 640 r／min，边界条件确定后，在Nastran中对涡轮盘的最大工作状态下的弹性应力、热弹性应力和周向应力分布进行计算。

3.2.1 弹性应力计算分析

高压二级涡轮盘在最大工作状态下的弹性应力分布如图2所示。

由计算结果可知，涡轮盘在最大工作状态下最大弹性应力出现在1／4辐板15 683节点处，最大等效应力为556 MPa，这与此处的厚度相对盘中心孔较薄且靠近过渡圆角有关，而且高压二级盘的传动安装边相对较大，位置靠近轮缘，转动时相对辐板产生较大的离心弯矩，从而在辐板接近过渡圆角处产生最大等效应力。

图2 高压二级涡轮盘弹性应力分布

3.2.2 热弹性应力计算分析

高压二级涡轮盘在最大工作状态下的热弹性应力分布如图3所示。

图3 高压二级涡轮盘热弹性应力分布

由图3可以看出，高压二级涡轮盘热弹性等效应力分布和弹性应力分布类似，也在15 683节点出现最大等效应力，最大应力为635 MPa，大于不考虑热应力时的弹性应力。由图2、图3可知，与单纯考虑离心力相比，考虑热应力的计算结果中等效应力最大值变大，最大值发生部位没有发生变化。在轮缘及中心孔处的应力值变小，这是由于离心载荷部分抵消了热应力的影响。其他部位的应力分布状况基本没有变化，只是数值大小发生变化。由于传动安装边产生的离心弯矩影响，辐板前端面应力值较后端面大，有发生翘曲倾向，在辐板向中心孔过渡的圆角处应力梯度较大，中心孔后边应力值较中心孔前边大。径向拉伸应力最大值发生部位与等效应力最大部位相同，但仍在弹性范围内。

对高压二级涡轮盘的热弹性径向应力进行计算发现，高压二级涡轮盘在最大工作状态下的最大热弹性径向应力为735 MPa，大于在此状态下的最大等效应力635 MPa，最大径向应力和最大等效应力出现在同一个节点，因此进行低循环疲劳试验时，可将该部位作为考核点。鉴于试验条件的限制，试验时只能控制一个不随涡轮盘转速变化而变化的恒定的温度场，为了使标准循环载荷峰值时的温度与考核部位的温度相当，可将考核部位在最大工作状态下的有限元计算温度（800.02 K）作为低循环疲劳的试验温度。3.2.3 周向应力计算分析

高压二级涡轮盘在最大工作状态下的周向应力分布情况如图4所示。

图4 高压二级涡轮盘周向应力分布

由图4可知，涡轮盘内径处的周向应力为268.22 MPa，平均周向应力为219.76 MPa，辐板处的周向应力为401 MPa。按EGD－3应力标准规定：在所有正常工作条件下，涡轮轮盘的平均周向应力不大于75%σ0.1（σ0.1为产生0.1%残余变形的屈服强度）；在离心载荷及热载荷作用下，内径处的周向应力不大于95%σ0.1，辐板处的周向应力不大于85%σ0.1。而涡轮盘在设计转速状态下，内径处的温度为766.93 K，盘体平均温度为805.2 K，此时σ0.1在804 MPa～834 MPa之间［6］，因此在此计算工况下该涡轮盘满足EGD－3的静强度设计要求。

4 总结

本文建立了某型发动机高压二级涡轮盘的有限元模型，利用有限元方法分析了其在最大工作状态下的温度和应力分布，得出以下结论：

（1）高压二级涡轮盘1／4辐板处热弹性等效应力和径向应力在发动机最大工作状态下都是最大的，可作为低循环疲劳试验的考核部位，其工作温度可作为试验温度。

（2）高压二级涡轮盘在离心载荷和热应力作用下等效应力均在弹性范围内，满足EGD－3的静强度设计要求。

［1］ 苏清友.航空涡喷涡扇发动机主要零部件定寿指南［M］.北京：航空工业出版社，2004.

［2］ 李朝阳，张艳春.燃机涡轮盘三维瞬态温度及应力场计算分析［J］.动力工程，2006，26（2）：211－214.

［3］ 李水姣.某型燃气轮机低压涡轮盘强度分析［J］.机械工程与自动化，2012，174（5）：37－39.

［4］ 王利民.涡轮盘蠕变／疲劳寿命预测和试验验证［D］.北京：北京航空航天大学，2000：35－40.

［5］ 徐可君，叶新农.航空发动机综合飞行换算率的确定［J］.推进技术，2006，27（1）：24－29.

［6］ 《中国航空材料手册》编辑委员会.中国航空材料手册（第2卷）［M］.第2版.北京：中国标准出版社，2002.