正多边形量子环链自旋输运性质研究

要晓腾，张 伟，刘建军，3

（1.河北师范大学 物理科学与信息工程学院，河北 石家庄 050024；2.河北广播电视大学 开放学院，河北 石家庄 050071；3.石家庄学院 物理与电气信息工程学院，河北 石家庄 050035）

正多边形量子环链自旋输运性质研究

要晓腾1，张 伟2，刘建军1，3

（1.河北师范大学 物理科学与信息工程学院，河北 石家庄 050024；2.河北广播电视大学 开放学院，河北 石家庄 050071；3.石家庄学院 物理与电气信息工程学院，河北 石家庄 050035）

研究了考虑Rashba自旋轨道耦合的任意正多边形量子环链的自旋输运性质.当不考虑Rashba自旋轨道耦合时，量子环链中电子的透射电导不发生自旋极化和翻转；当考虑Rashba自旋轨道耦合时，Rashba自旋轨道耦合可以控制量子环链中电导的极化.点连接的量子环链透射电导存在奇偶震荡现象，线连接的量子环链透射电导的极小值不随链长度变化.

Rashba自旋轨道耦合；正多边形量子环链；自旋输运性质

0 引言

半导体自旋电子学[1，2]在低维半导体物理中迅速崛起，主要涉及电子自旋输运、自旋极化电子注入等方面的研究.随着半导体纳米技术的迅猛发展，在电子输运方面，半导体中电子的自旋性质已经引起越来越多的关注，科学家们希望可以设计出一类以电子自旋为基础的电子器件，外加磁场可以引起介观半导体材料中电子的Zeeman能级劈裂.所以，通过调控外加磁场可以实现介观半导体材料中自旋输运的相干调控.而调控纳米尺寸器件中的外加磁场非常不方便，所以，需要构建一种在没有外加磁场时，也能实现对自旋输运进行相干操控的自旋过滤器件.由于在半导体材料中有自旋轨道耦合，固体材料中结构反演不对称产生Rashba自旋分裂，从而能够通过改变外场而改变耦合强度以达到操控电子自旋取向的目的；而电子的自旋极化比较容易在稀磁半导体或铁磁半导体材料中实现.因此，自旋极化电流注入、自旋的操控以及测量成为半导体器件中的重要问题.在这方面具有代表性的概念器件是Datta提出的自旋场效应晶体管.近年来关于自旋电子器件不断有新的理论模型和研究热点被提出，并已成为自旋电子学发展的动力.

由于电子在量子网络中传输时表现出一些有趣的特征[3-7]（如量子干涉），使得量子环中的电子输运性质受到广泛关注.Aeberhard等人[8]研究了存在Rashba自旋轨道耦合的圆形量子环的自旋输运性质.除了基于圆形量子环的自旋输运性质研究，基于多边形量子环和多边形量子环链的自旋输运研究也得到了人们的广泛关注.Bercioux等人[9]讨论了一维菱形链量子网络模型，发现存在Rashba自旋轨道耦合作用时电子的局域化现象.但是，理论调研发现，基于任意多边形量子环链的自旋输运性质还没有学者研究，尤其是任意多边形量子环链中量子环之间耦合方式对于输运性质的影响还没有被讨论和研究过.因此，以任意多边形量子环链模型为基础，我们主要研究了存在Rashba自旋轨道耦合的正多边形量子环链的自旋输运特性.

1 模型和基本公式

考虑如图1所示量子网络模型，研究正多边形量子环链的自旋输运问题.长度相等且均为l的一维量子线在x-y平面内连接成正多边形量子网络.环内量子线及连接环的节点上考虑Rashba自旋轨道耦合.左右外界电子通过入射和出射引线分别连接到多边形量子环的节点0和m上.在左右两端电子库零偏压极限下形成由左到右的电流，忽略子带杂交效应且假定量子线是单通道的[9]，电子沿方向量子线上的哈密顿量可表示为[10]

图1 （a）任意正多边形量子环通过共享1个节点组成量子环链（点连接的量子环链）的结构图；（b）任意正多边形量子环通过共享1个边组成量子环链（线连接的量子环链）的结构图.电子由第1个环入射，由第m个环出射，链长为m，表示由m个正2N边量子环连接

边形量子环平面的z轴正方向的单位矢量，而kso描述Rashba自旋轨道耦合强度.

考虑能量为E的电子由节点0射入多边形量子环链时，两个端点引线的波函数可以分别表示为：

考虑到概率流守恒的普遍要求，它需要满足节点a处的连接条件，即Griffith边条件[11，12]：

其中符号表示求和涉及与节点a直接相连的所有节点b，将（3）式的波函数代入（4）式可以得到关于任意内部节点a的方程

其中

将（2）式定义的引线波函数代入（4）式，得波函数在节点0，m分别满足方程

其中M0，0，Mm，m，M0，b和Mm，b等可由（6）式中的节点a分别替换成0，m并对他们的最近邻节点求和而得到.

解上述线性方程组可得到电子的透射系数和反射系数.

然后我们根据Landauer-Büttiker公式[13]求出电导，其中别表示自旋向上和自旋向下的透射电导.

2 数值分析

基于上面的电导公式我们可以得到自旋电导G↑和G↓随总波矢kl的变化曲线.当不存在Rashba自旋耦合（ksol=0）时，点连接的量子环链（N=2，m=3）结构的电导随入射波矢的变化关系如图2所示，其中取G0=为电导单位，当入射电子为非极化流时，通过量子环链的透射电子电导G↑=G↓，自旋流并不会发生劈裂现象.由计算可以得出，当入射电子自旋全部为自旋向上的电子时，透射电子的自旋方向不发生偏转，透射电导只有G↑，而G↓=0.因此，不存在Rashba耦合（ksol=0）时，透射电子与入射电子自旋方向相同，没有出现自旋反转.此外，通过计算发现，当Rashba自旋轨道耦合强度为零时，线连接量子环链的透射电导也不会发生自旋劈裂现象，结论与点连接的量子环链情况相同.

存在Rashba耦合（ksol≠0）时，量子环链电导随入射波矢的变化关系如图3所示.图3（a）给出了点连接的菱形量子环链（N=2，m=3时）电导随入射波矢的变化曲线，图3（b）、（c）、（d）分别表示点连接的正六边形量子环链（N=3，m=3，4，5时）电导随入射波矢的变化曲线.对比图3（a）和（b）可以看出，边数增加的正多边形量子环的点连接量子环链的电导震荡曲线更加剧烈.这说明，区别于单个多边形量子环的自旋输运性质[14]，正多边形量子环链的透射电导与多边形环的边数相关.由图3（b）、（c）、（d）可以看出电导呈周期性振荡且随着量子环链中量子环数量的增加电导的振荡频率增加，当链长m为偶数时，在kl=1.5π处电导出现极大值；当链长m为奇数时，在 处电导出现极小值.这表明，点连接的正多边形量子环链存在电导的奇偶震荡现象.此外随着链长度的增加，电子的自旋极化强度增强，出现了完全的自旋极化透射电导.

在Rashba自旋轨道耦合（kso≠0）时，但多边形量子环的耦合方式变为线连接量子环链，量子环链电导随入射波矢的变化关系如图4所示.其中多边形量子环之间以共享1根量子线的形式耦合.图4（a）、（b）和（c）分别表示N=2，m=3，4，5时电导随波矢的变化曲线.对比图3（a）和图4（a），发现图4（a）大概在kl=1.4π，1.5π，1.6π处出现电导极小值.这说明改变多边形量子环耦合方式使得量子环链的耦合强度变大，使得电子局域化增强，电子局域在量子环内无法透射而形成了电导极小值.对比图4（a）、（b）和（c）可以看出，随着多边形量子环链长度的增加，电导极小值的位置保持不变.这说明对于以共享1根量子线的形式耦合的多边形量子环链的电导极小值仅与自旋轨道耦合以及环结构相关，与多边形量子环链长度无关.

图2 当Rashba自旋轨道耦合强度为零 （ksol=0）时，在点连接的量子环链（N=2，m=3）体系中，自旋电导随入射波矢的变化

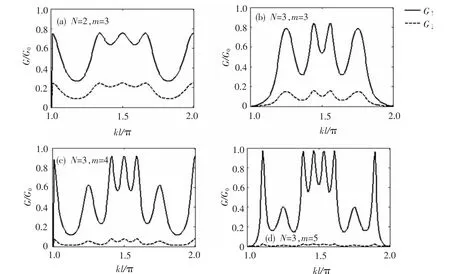
图3 存在Rashba自旋轨道耦合（ksol=0.02π）时，点连接的多边形量子环链电导随入射波矢的变化关系.入射电子为非极化电子流，实线为自旋向上的透射电导，虚线为自旋向下的透射电导

图4 存在Rashba自旋轨道耦合（ksol=0.02π）时，线连接的多边形量子环链电导随波矢的变化关系.入射电子为非极化电子流，实线为自旋向上的透射电导，虚线为自旋向下的透射电导

3 结论

运用量子网络的典型方法和Landauer-Büttiker电导公式对正N边形量子环链的输运特性进行了研究.结果表明：在不存在Rashba自旋轨道耦合情况下，透射电导不会发生自旋劈裂现象.存在Rashba自旋轨道耦合时，点连接的正多边形量子环链存在电导的奇偶震荡现象；线连接的的正多边形量子环链的电导极小值仅与自旋轨道耦合以及量子环结构相关，与多边形量子环链的长度无关.

[1]PRINZGA.Magnetoelectronics[J].Science，1998，282：1660-1663.

[2]WOLF S A，AWSCHALOM D D，BUHNNAN R A，et al.Spintronics：A Spin-Based Electronics Vision for the Future[J].Science，2001，294：1488-1495.

[3]WANGHX，XIONGSJ.ScalingBehaviorofChargeandDpinConductanceofaTwo-dimensionalNetworkwithRashbaSpin-orbitCoupling[J].Phys.Rev.B，2006，73（4）：045321.

[4]TANGHZ，ZHAILX，SHENM，etal.EffectsofRashbaSpin-orbitCouplingandaMagneticFieldonaPolygonalQuantumRing[J].Phys. Lett.A，2014，378（37）：2790-2794.

[5]TANG H Z，ZHAI L X，LIU J J.Transport Properties in a Multi-terminal Regular Polygonal Quantum Ring with Rashba Spin Orbit Coupling[J].Chin.Phys.B，2012，21（12）：120303.

[6]WANG H X，XIONG S J，Evangelou S N.Spin Filtering in Four-terminal Wire Networks with Spin-orbit Coupling[J].Phys.Lett.A，2006，356（4-5）：376-381.

[7]ZHAILX，WANGY，LIUJJ.EffectofRashbaSpin-orbitCouplingonElectronTransportinAsymmetrically Coupled Regular Polygonal QuantumRing[J].Phys.Lett.A，2010，374：4548.

[8]AEBERHARDU，WAKABAYASHIK，SIGRISTM.EffectOfSpin-orbitCouplingonZero-conductanceResonances in Asymmetrically CoupledOne-DimensionalRings[J].Phys.Rev.B，2005，72（7）：075328.

[9]BERCIOUX D，GOVERNALE M，CATAUDELLA V，et al.Rashba-Effect-Induced Localization in Quantum Networks[J].Phys.Rev. Lett，2004，93（5）：056802.

[10]MIRELES F，KIRCZENOW G.Ballistic Spin-polarized Transport and Rashba Spin Precession in Semiconductor Nanowires[J].Phys. Revs.B，2001，64（2）：024426.

[11]FUHRERA，LüESCHERS，IHNT，etal.EnergySpectraofQuantumRings[J].Nature（London），2001，413（6858）：822.

[12]BüTTIKER M，IMRY Y，LANDAUER R.Generalized Many-channel Conductance Formula with Application to Small Rings[J].Phys. Rev.B，1985，31（10）：6207-6215.

[13]FRUSTAGLIA D，RICHTER K.Spin Interference Effects in Ring Conductors Subject to Rashba Coupling[J].Phys.Rev.B，2004，69（23）：235310.

[14]TANG H Z，ZHAI L X，LIU J J.Spin Transport Properties of Polygonal Quantum Ring with Rashba Spin-orbit Coupling[J].J.Appl. Phys.，2013，114：023702.

（责任编辑 钮效鹍）

A Research on the Spin Transport Oroperties of Polygonal Quantum Ring Chain

YAO Xiao-teng1，ZHANG Wei2，LIU Jian-jun1,3
（1.School of Physical Science&Information Engineering，Hebei Normal University，Shijiazhuang，Hebei 050024，China；2.Open School，Hebei Radio&TV University，Shijiazhuang，Hebei 050071，China；3.School of Physics&Electrical Information Engineering，Shijiazhuang University，Shijiazhuang，Hebei 050035，China）

The spin transport properties of the equilateral polygonal quantum rings chain with Rashba spin-orbit coupling are studied.The spin polarized conductance can not occur when the Rashba spin-orbit coupling is not considered.When the Rashba spin-orbit coupling is considered，the spin polarization of the conductance in a polygonal quantum rings chain can be controlled by the Rashba spin-orbit coupling.And odd-even parity oscillations of spin polarization of the electrons through the point connected quantum rings chain are found.In addition，the location of the minimum conductance of the side connected quantum rings chain is independent with the length of the chain.

Rashba spin-orbit coupling；polygonal quantum rings chain；spin transport property

O471.1

：A

：1673-1972（2014）06-0011-05

2014-08-04

国家自然科学基金（61176089）；河北省自然科学基金（A2011205092）

要晓腾（1988-），女，河北南和人，硕士研究生，主要从事低维半导体输运研究.