追问，让数学课堂更具实效

杨春东

由于人们的思维或求知都是从问题开始的，因此在初中数学课堂教学中，教师的首要任务就是激发学生对问题的思考.而怎样提出问题才更能激发学生的思考呢？凭借多年的教学实践，笔者认为，提问中追问是最能激发学生思维的一种手段.

追问，即对某一问题或某一内容，在一问之后又二次、三次等多次追问，“穷追不舍”，它是在对问题深入探究的基础上追根究底地继续发问.追问不是一般的对话，对话是平铺直叙地交流，而追问是对事物的深刻挖掘，是逼近事物本质的探究.就教学来说，追问是围绕教学目标，设置一系列问题，将系列问题与课堂临时生成的问题进行整合，巧妙穿插，进行由浅入深，由此及彼地提问，以形成严密而有节奏的课堂教学流程.

在数学教学中，教师适时有效的追问，可以点燃学生思维对话的激情，激活学生沉睡的个体知识，促进学生思维水平的提升，让数学课堂更具实效.

一、循序追问，开启智慧

在教学中，既能接受挑战又能挑战别人思维的对话才是最有活力的，而追问正是在思维碰撞点上演出的生动事件，它追求的是思维的深度和广度，可以培养学生思维的深刻性、敏捷性.当教师发现学生的回答肤浅、粗糙、片面甚至是错误时，就应紧追不舍再次发问，促使并引导学生就原来的问题进行深入的思考.

例如，“有理数加法法则”教学片断.

一直蜗牛沿数轴爬行，它现在的位置恰好在原点：（1）先向右爬行5cm，再向右爬行3cm；（2）先向左爬行5cm，再向左爬行3cm；（3）先向右爬行5cm，再向左爬行3cm；（4）先向左爬行5cm，再向右爬行3cm；（5）先向右爬行5cm，再向左爬行5cm；（6）先向左爬行5cm，再向右爬行5cm；（7）第一秒向右爬行5cm，第二秒原地不动；（8）第一秒向左爬行5cm，第二秒原地不动.上述八种情况下，两次爬行的结果是什么？请同学们借助数轴研究蜗牛的各种运动情况.

（学生展示画好的图）

追问1：同学们看了有什么建议吗？

生1：把爬行方向用箭头表示出来，两次运动后的结果也要用带箭头的线段来表示.

追问2：同学们能把蜗牛运动的情况和运动后的结果用算式表示出来吗？

生2：（1）5+3=8；（2）5+3=8；（3）5-3=2；（4）5-3=2；（5）5-5=0；（6）5-5=0；（7）5+0=5；（8）5+0=5.

生3：我认为不对.上面这些算式没有发映出蜗牛的运动方向.

追问3：那该怎么办呢？

生4：规定向右为正，向左为负，这些算式可以写成（1）（+5）+（+3）=+8；（2）（-5）+（-3）=-8；（3）（+5）+（-3）=+2；（4）（-5）+（+3）=-2；（5）（+5）+（-5）=0；（6）（-5）+（+5）=0；（7）（+5）+0=+5；（8）（-5）+0=-5.

追问4：看来同学们考虑问题很细致.下面请你们观察这八个算式，分析每个算式中加数的符号与和的符号，加数的绝对值与和的绝对值之间的关系，把你的发现用语言表述出来，相互交流补充.

……（学生交流过后，教师继续追问）

追问5：我们把刚才总结的（1）～（8）再分析一下，能否更精炼些？

生5：分成三类，（1）（2）是同号两数相加，（3）（4）（5）（6）是异号两数相加，（7）（8）是一个数和零相加，这样简练些.

追问6：同学们想一想，同学们归纳的这些特点对我们有什么帮助？

生6：可以用来进行有理数的加法运算.

追问7：这就是加法运算法则，根据我们的总结，在进行运算时，一般分几步？

生7：两步，先定符号，再算绝对值.

教师通过一系列的追问，关注数学知识的内在联系，让学生对已有的知识体系不断扩展，学生对所学的新知识达到了真正的理解和掌握.教师的追问开启了学生的智慧，掀起了课堂的高潮，演绎了课堂的精彩，提高了教学质量.

二、发散追问，以点带面

带领学生走到“记忆”背后的有效捷径之一是经常向学生提出“发散性”的问题 ，引导学生通过运用知识和经常性的实践，养成高层次思维的行为习惯.

例题的教学并不是为了求解题目，而是要通过题目的求解和评价达到巩固知识、训练能力的功效.所以不能就题讲题，否则方法单一、知识零碎，不利于学生系统掌握.在例题教学中，运用追问的方式，以所讲问题为点向外发散，以点带面，带出与该知识点相关的一系列问题，从而便于学生形成知识网络，提升例题的价值.

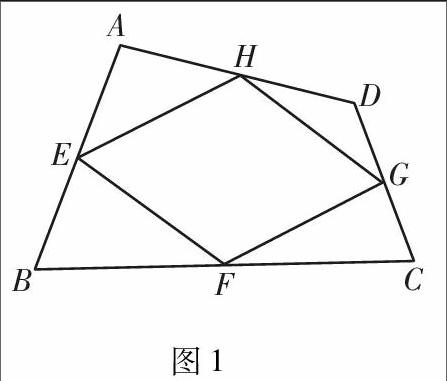
例如，已知：如图1，在四边形ABCD中，E、F、G、H分别为AB、BC、CD、DA的中点，求证：四边形EFGH是平行四边形.

分析：对于这个问题，学生不难证明，但教学不能到此为止，可以设计如下问题追问学生.

追问1：还有其他证明方法吗？

追问2：分别顺次连接以下四边形的四条边的中点，所得到的是什么四边形？（1）平行四边形 ；（2）矩形 ；（3）菱形；（4）正方形；（5）梯形 ；（6）直角梯形 ；（7）等腰梯形.

追问3：从中你们能发现什么规律？

追问4：顺次连接n（n≥4）边形的各边中点，能得到怎样的n边形？顺次连接正n边形各边中点，得到的是什么多边形？是正多边形吗？

追问5：从上述问题的解决过程中，你能得到哪些启示？

通过追问，学生重温了三角形中位线性质定理，复习了特殊四边形的性质，拓展延伸到多边形的性质.可见，通过发散追问，许多知识点可以连成线、结成网，使学生的知识和能力均能多点激活，从而提高学生的学习能力，保证了课堂教学的效益.

三、变式追问，拓展视野

许多数学问题的本质不会随非本质因素的变化而变化，它们所使用的方法或模型是基本稳定的.在教学中，我们要通过问题变式的追问，让学生去总结提炼出这些本质的因素，让学生面对纷繁多变的题目能“以静制动”，让学生体会那种看透本质的成就感.

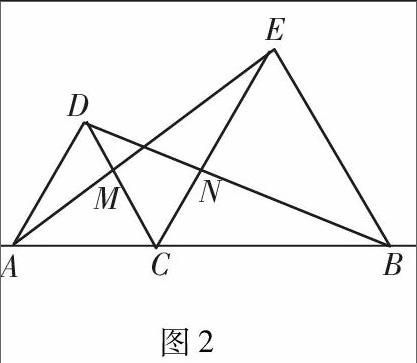
例如，如图2，A，B，C三点在一条直线上，△DAC和△EBC均为等边三角形，AE，BD分别与CD，CE相交于点M， N，有如下结论：①△ACE≌△DCB；②CM=CN；③AC=DN.其中，正确的结论有（）.

A.3个B.2个C.1个D.0个

分析：该题意在考查学生掌握全等三角形知识的情况，若只是就题论题，则不能充分发挥它的价值.所以，我们应该趁热打铁，变式再追问，让学生在变式追问中总结该类问题的解决办法.

追问1：图2中全等的三角形有几对？

追问2：如图3，连接MN.（1）猜想△CMN的形状.（2）猜想MN和AB的位置关系.（3）猜想∠EFB的度数.（4）相似的三角形有哪些？（5）若已知△DAC和△EBC的边长分别为a和b，试求MN的长.

变式1：如图4，当A，B，C三点不共线时，以上探讨的一系列结论哪些仍然成立？哪些不成立？

变式2：如图5或图6，已知：△ABD、△ACE都是等边三角形，求证：CD=BE.

变式3：如图7，点A为线段CB延长线上一点，分别以BC，AC为边在直线BC的异侧作等边△BCD和等边△ACE，求证：AD=BE.

变式4：如图8，点A为线段BC上一点，△ABD和△ACE都是等腰三角形，且AB，AD与AC，AE分别是等腰三角形的腰，且△ABD∽△ACE，求证：CD=BE.

变式追问，可以从多角度入手，可以变化题目条件，也可改变题目设问，若在复习过程中，还可以在知识上有较大的跨度.

心理学研究表明，新的事物容易使人产生兴趣，激发求知欲，因此在复习阶段教师因调整知识结构，将知识以另一幅“面孔”呈现在学生面前，使学生再次产生新鲜感，增强他们的求知欲.在上面的案例中，对一道典型题勤于变式追问，就可将前后所学知识融会贯通，学生能透过纷繁的表象看到问题的实质，有一种万法归宗的感觉，并开拓了自己的视野.

总之，在数学教学过程中，我们应积极地对问题进行“二次开发”，不断地延伸问题、叠加问题、形成问题链、问题组，适时、有效地进行追问，不对的要追错，正确的要追因，肤浅的要追根，从而不断地激活学生的思维.“问”出学生的思维，“问”出学生的激情，“问”出学生的创造，“问”出有效的课堂.