基于小波分析的热障涂层厚度超声检测
郑金华,高鸿波,张士晶,石 剑,王 婵
(1.无损检测技术教育部重点实验室(南昌航空大学),南昌 330063;2.中航工业南方航空工业(集团)有限公司,湖南 株洲 412002;3.西安航空动力股份有限公司,西安 710021)
0 引言
热障涂层是一种陶瓷涂层,广泛应用于发动机叶片等热端部,作为提高其工作温度而采取的一种有效措施,目前应用最广的热障涂层材料是在氧化锆(yttria stabilized zirconia,YSZ)中掺6%~8%氧化钇成分[1]。涂层的均匀性、孔隙率、厚度等参数直接影响到其隔热效果,如何采取无损测量方法测量涂层厚度已成为该领域的重要任务。热障涂层的厚度通常只有几十到几百μm,使用超声波垂直入射到多层薄介质(水/涂层/粘结层/基体)中时,必定会在各异质界面产生多次反射波和透射波,使得涂层两侧界面的反射回波相互叠加、干涉,在时域信号里面难以区分[2-3]。目前国内针对该问题采用的方法通常为频谱分析法。由于傅里叶变换只适用于平稳信号,且对信号的奇异性不敏感,而超声波探伤仪采集到的回波信号为非平稳信号[4];小波变换具有良好的时频局域特性、品质因素恒定、多分辨率等一系列优点而被称为“数学显微镜”[5]。经研究表明对小波变换求模极大值能较精确的检测信号的奇异点,再配合Lipschitz指数α对信号奇异点的判断[6],从而有可能从超声信号中提取出和涂层厚度有关的参数。
1 连续小波变换模极大值检测信号奇异性理论
1.1 连续小波变换
连续小波变换作为信号时频分析的重要工具。它能够根据信号频率的高低自适应选择时间窗大小;高频时选择宽窗,低频时选择窄窗[7];因此,在分析信号因瞬变而产生的高频信息时,小波变换比傅里叶变换能够更好的观察细节信息。
设Ψ(t)∈L2(R)(L2(R)表示平方可积的实数空间,是在能量上有限的空间信号),其Fourier变换为(ω)。当(ω)满足容许条件
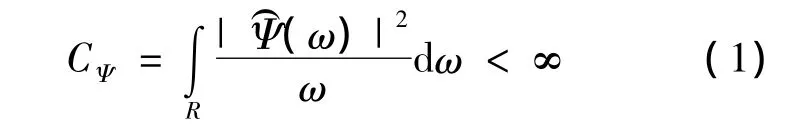
此时,称Ψ(t)为基本小波或者母小波。将母小波Ψ(t)经过伸缩和平移后得到
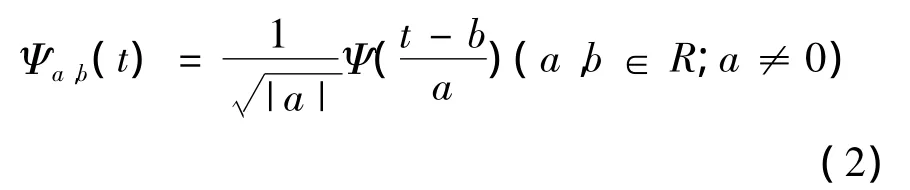
Ψa,b(t)是母小波Ψ(t)经过伸缩和位移产生的一组新函数,称之为小波基函数,简称为小波基。其中,a称为伸缩因子或者尺度因子,b为平移因子。
对于任意信号的f(t)小波变换为
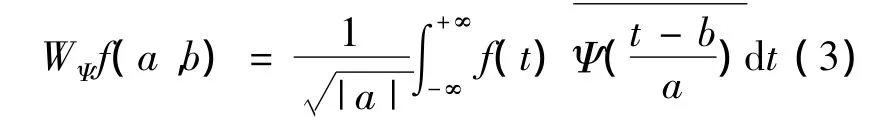
式中,Ψ(t )和Ψ(t)互为共轭。
1.2 连续小波变换模极大值检测信号奇异性理论
小波变换的定义也可以由卷积的方式给出。设:
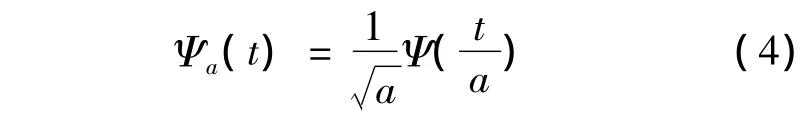
则信号x(t)的小波变换可以定义为:
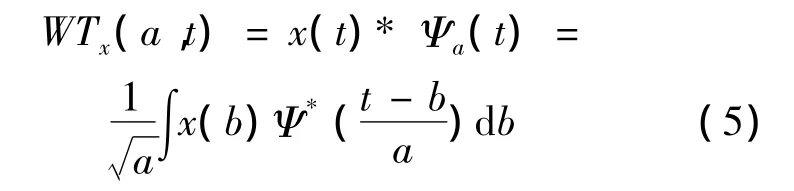
无论是从卷积还是内积来定义小波,对数据计算而言并没有本质的区别,而按卷积来定义优点是:一个信号经小波变换后就可以看成是信号通过一个系统的输出响应,而该系统的冲击响应就是式(4)中的Ψa(t),如图1所示。
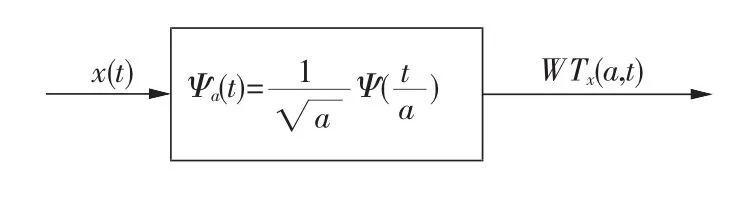
图1 小波变换的卷积表示Fig.1 Wavelet transform convolution representation
假设θ(t)为低通函数,并且具有高阶导数,令 Ψ(1)(t)=dθ(t)/dt,Ψ(2)(t)=d2θ(t)/dt2,可得出以下结论:
1)Ψ(1)(t)、Ψ(2)(t)是一个能作为母小波使用的带通函数;
2)信号经过一个低通滤波器平滑后再求N阶导数实际上就相当于直接用该平滑函数的N阶导数来滤波(N为正整数)。
函数的极值点对应着函数一阶导数的零点,而函数的拐点为函数二阶导数的零点。因此用Ψ(1)(t)对 x(t)作小波变换所得到(a,t)的,其过零点反映了x(t)的极值,同理,用Ψ(2)对x(t)作小波变换所得到的(a,t),其过零点反映了x(t)的转折点。从而可以实现用小波变换对信号x(t)的极值点和转折点的检测[8]。
要使信号的极值点或转折点在小波变换后的结果中体现出来,所选用小波函数应该为某一低通函数的一阶导数或者二阶导数,而Mexh小波正好满足此性质,因此可以选取Mexh小波对超声信号作小波变换,并取小波变换模极大值(Wavelet modulus maxima,WTMM)进行分析。
1.3 Lipschitz指数
对于给定的一个信号x(t),如何描述它在某一点或某一区间的规则性或奇异性,通常是对该点或该区间求微分,如果它们是可微的,则信号在该点或该区间就是规则性的,反之,则是奇异的。如果在该点或该区间可微的次数越高,则该信号在该点或该区间的规则性就越强。而Lipschitz指数就是被用来定量地描述函数的奇异性和规则性情况的。Lipschitz指数的定义如下[9]:
对于给定信号f(t),如果存在常数K>0及n=└α┘阶的多项式pt0(t),使得

称f(t)在t0处具有Lipschitz指数α。显然,Lipschitz指数α能够表示出信号在该点的奇异性程度。α越大,则信号f(t)在该点的变化就越平稳,反之,α越小,则信号f(t)在该点的变化就越激烈。通过式(6)可知,阶跃函数的α=0,冲激函数的α=-1,三角函数的α=1。Lipschitz指数α和信号f(t)在t0或区间[a,b]处的导数阶次越高,相应的α越大。在信号的特性上表述就是f(t)在此处越平滑。若f(t)在此t0处的Lipschitz指数α小于1,则信号在该处是不可微的,即具有奇异性。因此Lipschitz指数α可以作为信号在某一点或某一区间的规则性(或奇异性)程度的一个度量[10]。
2 试样制备及超声检测
2.1 试样制备
所用试样是在45钢基体,利用大气等离子喷涂方法先喷涂NiCrAlY粘结层后再以同样的喷涂方法喷涂ZrO2热障涂层。通过控制喷涂时间和喷涂速率可以控制热障涂层的厚度为80~150 μm。采用水浸超声检测系统对涂层厚度进行检测,相比于普通超声测量方法,水浸聚焦具有灵敏度高、分辨率高、重复性好等一系列有点。水浸平探头型号为I15P6CF30,其中心频率为15MHz,晶片直径d=6mm。采集卡型号为PicoScope 3207B,采样频率为250MHz。
2.2 超声检测
首先将试样放入水槽中,涂层面朝上,调整探头水平位置,将其置于涂层正上面且垂直涂层面;通过观察涂层表面的超声反射信号,再调整探头的垂直距离及信号增益,确保涂层在探头的焦点位置处以及此时的涂层表面声压反射信号在满刻度的80%;最后设置超声C扫描的范围和步距。
3 实验数据分析
3.1 信号处理
图2为实际采取到的涂层声压反射信号,由图2可以明显观察出,在时域信号中很难直接提取出和涂层厚度有关的参量,无法直接判断两界面回波位置。因此无法使用超声脉冲反射法直接计算涂层厚度。利用Mexh小波基对该时域信号进行连续小波变换,得到如图3所示的小波系数图。
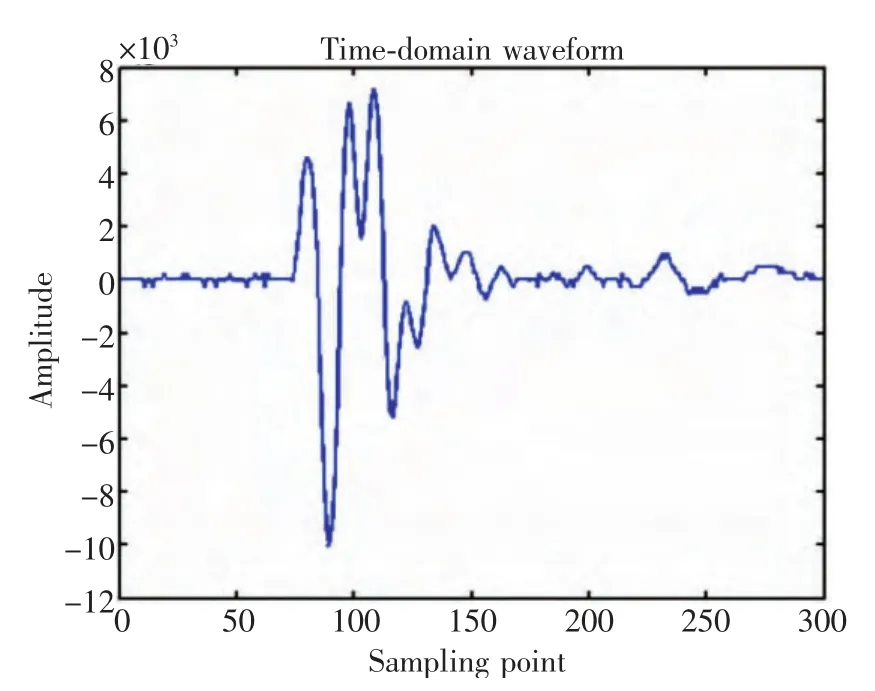
图2 超声检测时域波形图Fig.2 Time-domain waveform figure of ultrasonic date

图3 Mexh小波系数图Fig.3 Figure of Mexh wavelet coefficients
横坐标为采样点数,纵坐标为小波变换的尺度大小。先对图3中的整个小波系数取绝对值,再通过左右比较绝对值的大小找出局部模极大值,将这些模极大值用“1”代替,而非模极大值点则用“0”代替,并将其绘于与图3相同的坐标系中,得到如图4所示的小波系数局部模极大值图。图4中的黑点即为被“1”代替的模极大值点,而空白处即为被“0”替代的非模极大值点。如果信号在某时刻产生奇异性,则在图4中的模极大值连线将在较大尺度范围内变化。为了减小单一尺度确定奇异点带来的误差,对每一个采样点的所有尺度求取模极大值的平均值,得到平均幅值的大小代表各点奇异性程度。此信号的模极大值平均幅值如图5所示。
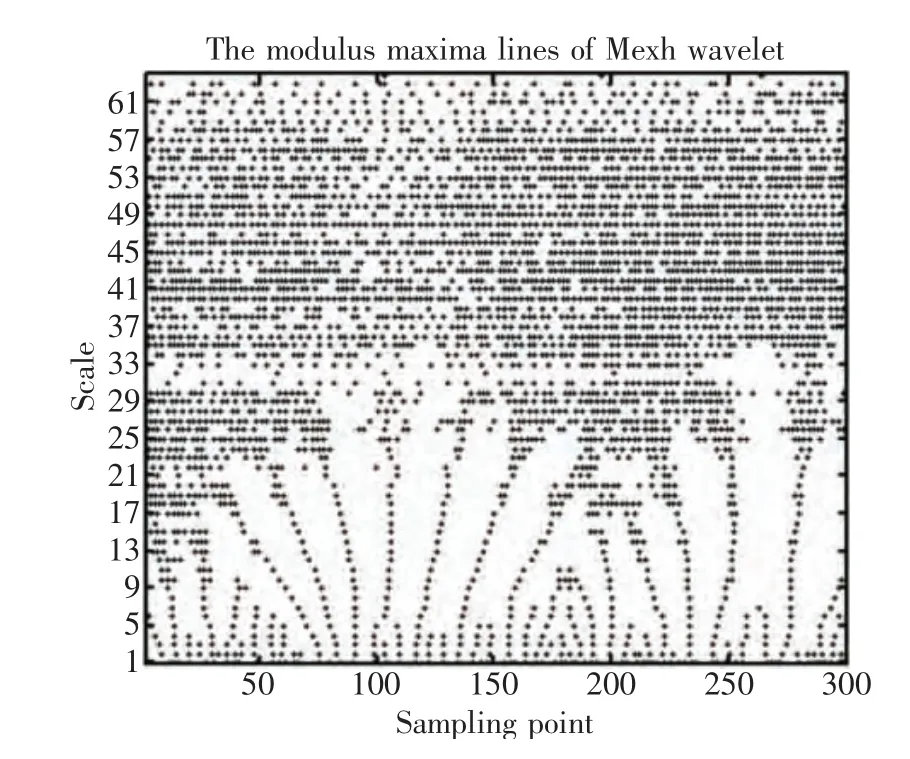
图4 Mexh小波模极大值线Fig.4 The modulus maxima lines of Mexh wavelet
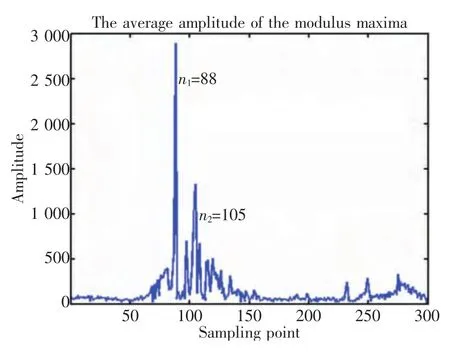
图5 模极大值平均幅值Fig.5 The average amplitude of the modulus maxima
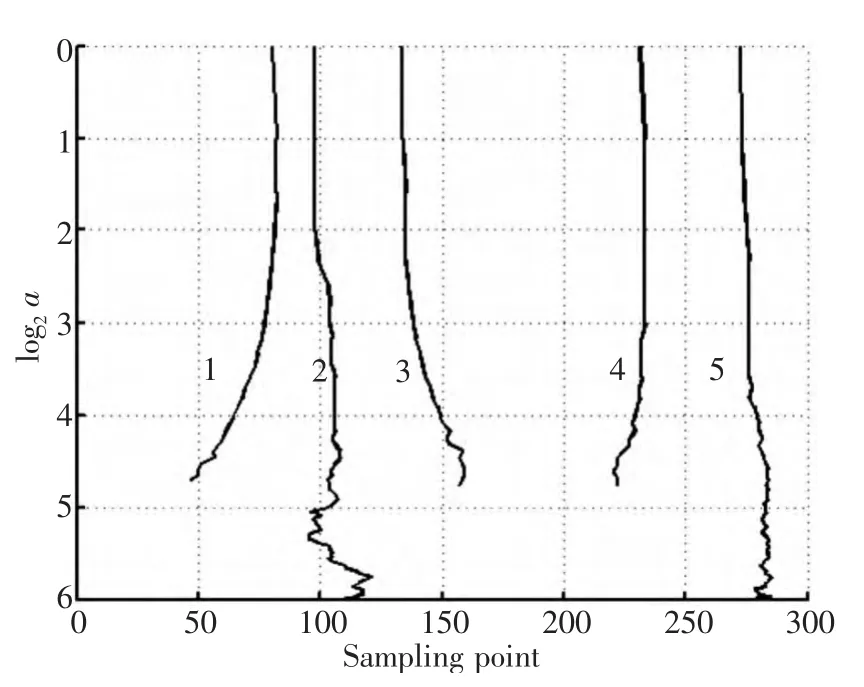
图6 模极大值线Fig.6 The modulus maxima lines
再对图4中的Mexh小波模极大值点求取的模极大值曲线,得到的模极大值曲线如图6所示,再对图6中的第一条模极大值曲线做一次多项式拟合,结果如图7所示(其他4条曲线同理),一次多项式的系数即为该拟合直线的斜率k,而Lipschitz指数α即为拟合直线的斜率k-0.5。由于有5条曲线,因此将得到5个斜率值和5个Lipschitz指数值,将这5个Lipschitz指数α绘于图中,结果如图8所示。
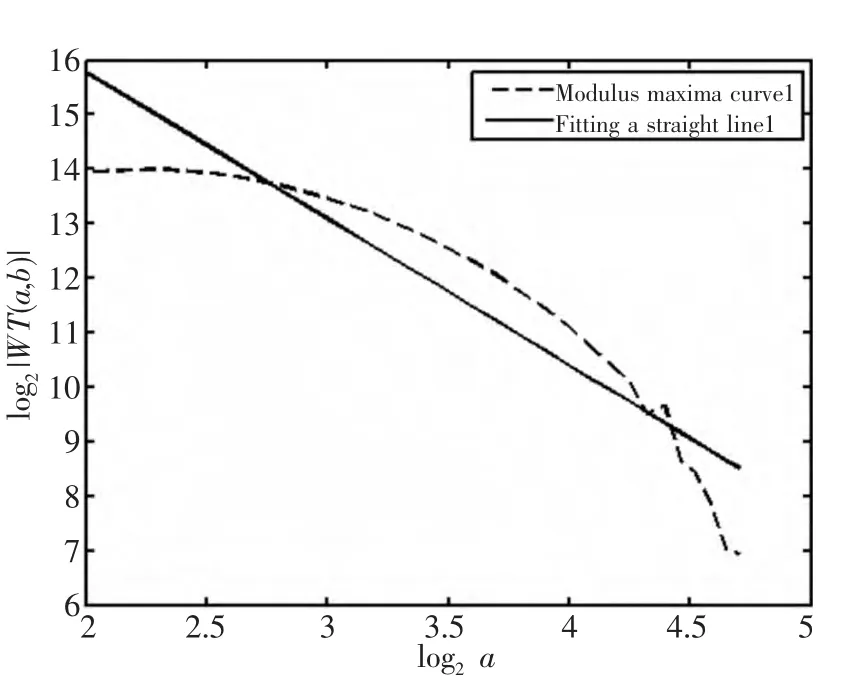
图7 直线拟合Fig.7 Fitting a straight line

图8 Lipschitz指数Fig.8 Lipschitz index

图9 SEM下涂层观测图Fig.9 Coating observation chart by using SEM
3.2 涂层厚度计算
可以利用这2种不同的方法对涂层进行测厚,即模极大值法和Lipschitz指数法。
模极大值法:由信号的突变原理可知,超声在在涂层的上、下界面处将产生奇异,小波系数模将取极大值,且极大值平均幅值最大。由图5中可知在n1=88、n2=105处都有局部小波系数模极大值平均值最大,能量最大,奇异性最大。依据小波变换模极大值检测信号突变的原理可以判断n1、n2分别对应着涂层上、下界面处的回波到达时间,从而确定超声在涂层中传播的时间。取涂层的声速v=3370 m/s,可以计算出涂层的厚度为114.6 μm。
Lipschitz指数法:从图8中可以看出,第1条和第2条模极大值曲线所对应的Lipschitz指数α分别为 α1=-3.2 和 α2=-2.1,都小于 1,因此这两条模极大值曲线所对应的点是奇异的。而这两条模极大值曲线所对应的点分别为n1=80和n2=98。同理,根据上述的超声测厚公式可以计算出涂层的厚度为121.3 μm。
3.3 SEM扫描电镜
对上述超声数据对应的热障涂层位置点上进行SEM扫描电镜实验,图9为该区域的扫描电镜结果图,从图中可以看出该点的实际厚度为118.4 μm。与小波变换模极大值法测得厚度的绝对误差为-3.8 μm,相对误差为3.2%。而与 Lipschitz指数法测得厚度的绝对误差为2.9 μm,相对误差为2.4%。YSZ试样不同位置下不同方法测量的结果见表1。
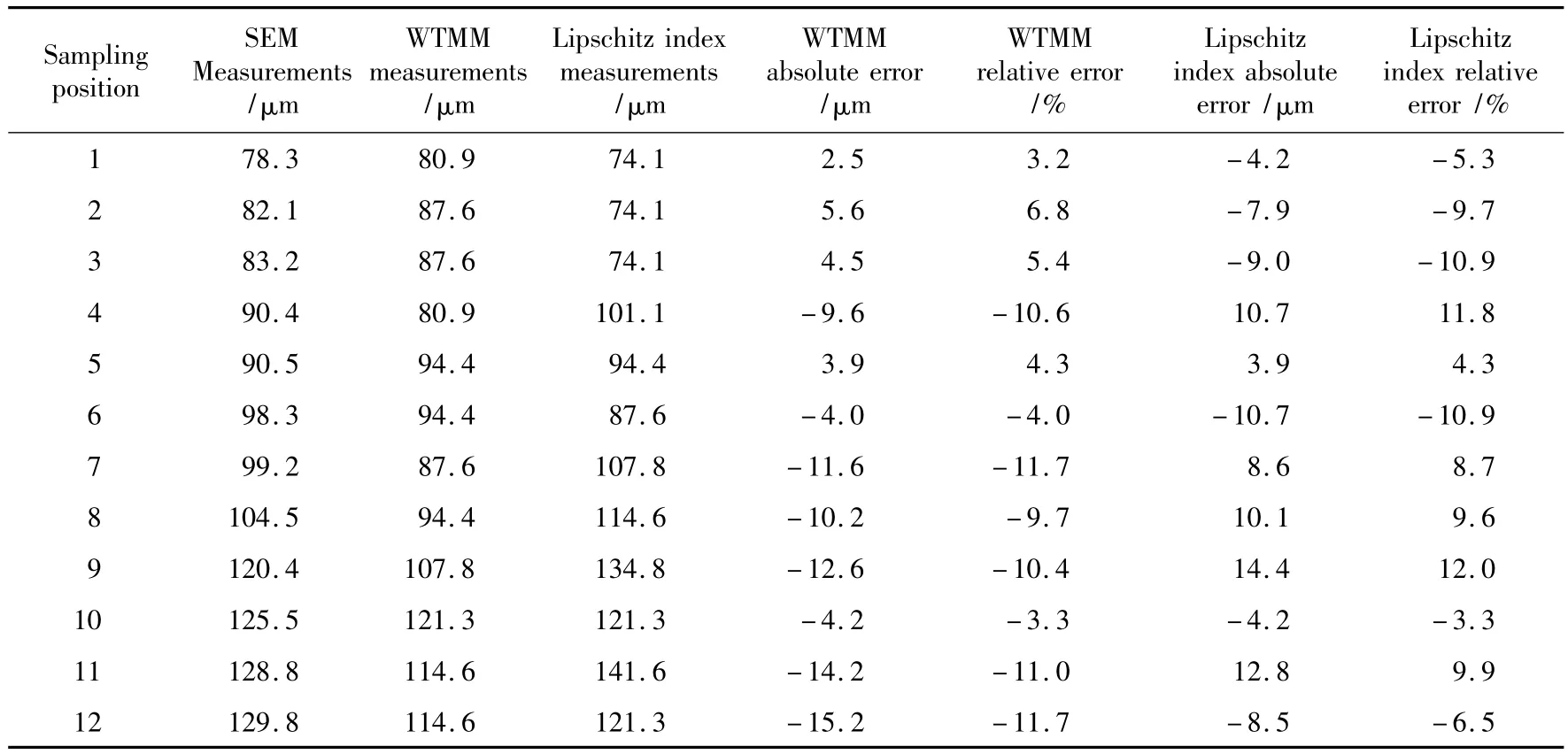
表1 不同方法下YSZ涂层试样厚度测量结果及厚度误差Table 1 Thickness measurement results and error of coating sample by different methods
为了便于观察,将表1中的3种测厚方法所得的结果绘于图中(图10)。从图10中可以看出,模极大值测厚结果相对于Lipschitz指数测厚的结果要均匀,且Lipschitz指数测厚的结果波动较大。
对于分别使用这两种方法所确定的信号奇异点的位置的差异,分析原因有:1)小波变换模极大值法是根据在每个时间点上对所有尺度的小波系数求取平均值的结果,给出的是一个奇异点的概率分布情况。也就是说,奇异点所在位置为模极大值平均幅值最大值位置的概率最大,并不代表奇异点就一定在该位置;2)Lipschitz指数给出的结果是根据一次多项式对模极大值曲线做直线拟合所确定的。对于不同的直线拟合方式,其斜率不一样,导致Lipschitz指数有所差异,影响对信号奇异点的判断;因此,使用这两种方法所确定的信号奇异点的位置会有所不同。
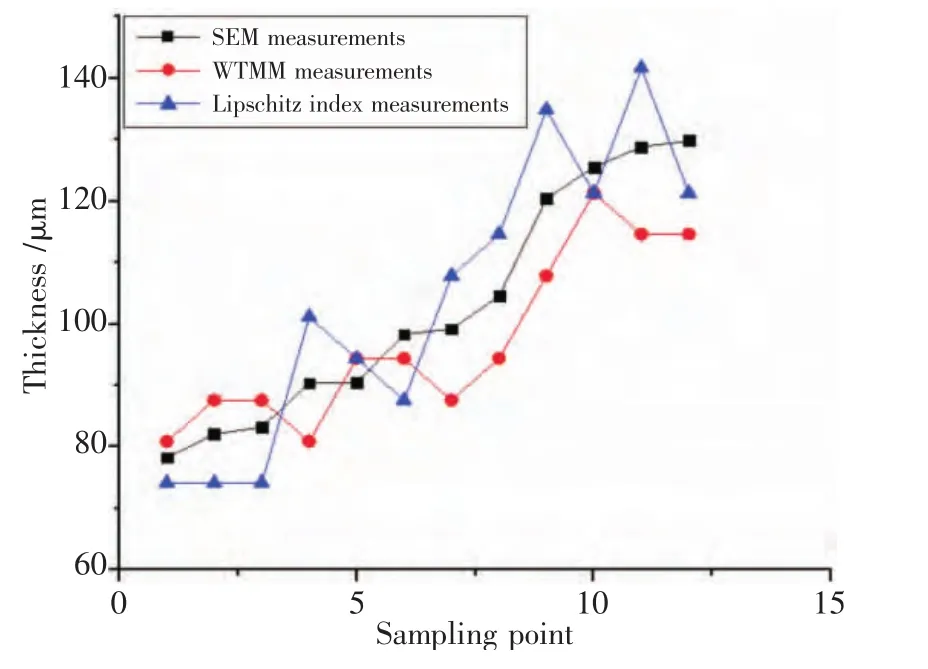
图10 不同方法测厚结果Fig.10 Thickness measurement results of coating sample by different methods
4 结论
1)可以利用小波变换模极大值法和Lipschitz指数法对涂层厚度在80~150 μm的热障涂层超声信号在不同界面处产生的奇异点进行检测。
2)本研究采用2种方法所测的涂层厚度值与扫描电镜测量值基本一致,2种方法都适用于分析使用超声测量热障涂层的厚度。
[1]Sohn Y H,Lee E Y,Nagaraj B A,et al.Microstructure characterization of thermal barrier coatings on high presser turbine blades[J].Surface and Coatings Technology,2001,146-147:132-139.
[2]林莉,李喜孟,赵扬.基于超声声速法的陶瓷涂层特性表征[J].理化检验:物理分册,2008,44(4):180-183.
[3]Han Z H,Wang H J,Zhou S K,et al.Characterization of functionally graded ZrO2thermal barrier coatings sprayed by supersonic plasma spray with dual powder feed ports[J].Journal of Central South University of Technology(Supple 2),2005,12(2):1-4.
[4]李喜孟,林莉,聂颖.薄层结构超声信号的小波分析[J].无损探伤,2006,30(4):53-56.
[5]杜晶晶,李晓延,史耀武.超声检测涂层厚度中小波变换模极大值法的研究[J].无损检测,2008,30(2):87-90.
[6]戴建新,郦志新,宋洪雪.基于小波的信号Lipschitz指数分析和应用[J].南京邮电大学学报:自然科学版,2008,28(6):69-73.
[7]周海林,徐毅成,刘美全.基于小波变换模极大值法的薄层材料超声测厚研究[J].仪表技术,2010(3):50-52.
[8]冯晓锋,张红岩,周原.基于尺度空域相关性的图像边缘检测[J].计算机工程与设计,2007,28(22):5455-5456.
[9]杨勇,郭吉强.Lipschitz指数与平稳小波变换在CT图像去噪中的应用[J].计算机工程与应用,2012,48(6):190-192.
[10]胡广书.现代信号处理教程[M].北京:清华大学出版社,2004:57-65.

