结构对变形镁合金减振性能的影响

王敬丰，李琳俊楠，鲁若鹏，潘复生

（1重庆大学 材料科学与工程学院，重庆400044；2重庆大学 国家镁合金材料工程技术研究中心，重庆400044）

随着航空航天、武器装备及交通工具等现代工业发展日趋轻量化、高速化和大功率化，由此引起的振动和噪声问题变得尤为突出。据统计，火箭、卫星失效约2／3的故障与振动和噪声有关［1］。同时，轻量化的结构易受振动影响从而降低隔音性能［2］。因此如何在零部件轻量化的同时降低噪声，改善人机工作环境已经成为当前急需解决的一个问题［3］。

镁及镁合金为目前密度最小的金属结构材料，同时具有明显优于其他结构材料的阻尼减振性［4－6］，在抑制机械振动和削弱波的传播以达到控制噪声和稳定结构方面被寄予厚望［7－9］，是最具有开发应用前景的商用轻质材料［10－14］。2008年，高云凯等［15］针对某轿车车身顶盖横梁，设计镁合金冲压件替代原钢结构横梁。通过有限元模拟得出，镁合金冲压件能达到原钢件同等的强度及顶压等，而且与原钢件相比减重约40%。随后，张力等［16］对具有相同结构的AZ91D镁合金试件和A380铝合金试件进行模态参数识别。结果表明：在几何结构相同的情况下，AZ91D镁合金试件具有更好的模态阻尼比。

以上这些研究，大多都针对材料本身，停留于材料替代的模拟或实验层面。由于镁合金材料刚性较低［16］仅通过直接的材料替换，其高阻尼减振性难以在实际工程中得到有效体现。因此，在保持镁合金良好阻尼特性的前提下，通过结构方面的合理优化设计试件，增强试件抗振能力，是目前镁合金大量应用于国防军工和民用工业过程中急需解决的问题。为使镁合金更加广泛地应用于生产生活，实现轻量化与减振的完美结合，本工作从模拟到实验验证，再到进一步模拟改进优化，对变形镁合金的减振性能进行研究。

1 不同结构镁合金型材的模拟分析

利用有限元分析软件，对相同材料不同筋板布置的镁合金型材进行瞬时动力学模拟分析。

1.1 有限模型的建立

1.1.1 数学模型

物体受力振动过程的数学模型为振动方程，根据瞬态动力分析的运动方程和通用方程：

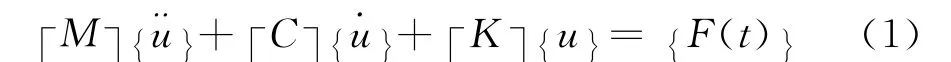
1.1.2 建模和网络划分

参考现有高速列车常用型材的筋板布置方式，设计模型形状名称如图1所示。网络划分采用六面体完全积分单元。

1.1.3 模拟参数设置

材料选择商用镁合金AZ31，弹性模量为45GPa，泊松比为0.35，密度为1.77×103kg／m3。进行相同面载荷3 MPa（作用时间0～0.2s），三角脉冲激励下的瞬时动态分析。

图1 各模型形状名称图 （a）梯形筋板模型；（b）矩形筋板模型；（c）三角筋板模型Fig.1 The shape and name of models （a）model with ladder reinforcing plate；（b）model with rectangular reinforcing plate；（c）model with triangle reinforcing plate

1.2 模拟结果与分析

图1（a），（b），（c）所示三种结构型材（以下简称a模型，b模型，c模型），前0.4s应力及位移的计算结果见表1，由表1观知，三种比较有代表性的筋板模型下板受力情况为：①有载荷作用时（t＝0～0.2s），a模型受力最大，b模型次之，c模型受力最小。②外载荷消失后（t＝0.2～0.4s），除b模型在0.25s时有一定上升的浮动，其余型材受力皆为下降趋势，c模型的镁合金型材受力持续保持较低的状态。总体而言，模型受力情况：a＞b＞c。选择各模型受力最大时刻的云纹图（图2）观察，三种模型受力最大的地方皆为筋板与壁板的连接处，可见，筋板与壁板之间的接触容易产生应力集中。其中，由于倾斜筋板的布置使得相同壁板长度内筋板与壁板的连接点比垂直筋板布置的模型少，从而产生了筋板与壁板造成的应力集中区域范围较小的情况。结合表1中数据，a模型虽然应力集中区域较少，但所受应力值较大，甚至超过垂直筋板布置的b模型，分析认为是由于筋板间的间距较大造成的。同是倾斜筋板的c模型和a模型，由于a模型筋板间距较小，下壁板所受应力明显降低。因此，影响下壁板受力的因素为筋板的斜度和筋板间的距离。

由表1可以看出，三种模型下板位移情况为：①有载荷情况下，c模型位移最小，a模型位移次之，b模型位移最大。②外载消失模型自由振动时，a模型最大位移在0.25s和0.35s时有一个短暂的往复升高，其余时间都呈下降的趋势。b模型在0.35s时有一个位移升高的点，其余时刻位移皆为下降趋势。c模型位移一直保持较低的接近零位移状态，下板振动最不显著。总体而言，模型下壁板位移情况：b＞a＞c。图3为各模型初始状态与最大变形（t＝0.10s）处的纵向截面的位移云图，由图3对比可见，三种模型的最大变形位置都为模型中部，且上下壁板一起变形。其中，b模型变形程度最大，下壁板最大位移达到13.040mm（表1），a模型变形程度次之，为10.59460mm，c模型的变形程度最小，最大位移仅有1.9440mm。

表1 各模型前0.4s内应力与位移对比表Table 1 Results of stress and displacement of models in 0.4s

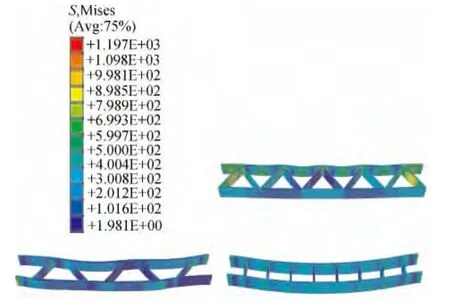
图2 各模型最大变形处（t＝0.10s）受力云纹图Fig.2 Stress moire diagram of models in the maximum deformation（t＝0.10s）

图3 模型初始状态与最大变形（t＝0.10s）位移云纹图Fig.3 Displacement moire diagram of models in the maximum deformation（t＝0.10s）

通过对不同筋板布置镁合金型材的动态模拟可知，综合受力、位移及整体变形方面考虑，三角筋板布置的镁合金型材的减振性能最好，梯形的次之，矩形最差。建议镁合金型材选择筋板布置时，在实际条件允许的情况下选择三角形的筋板结构。在受力要求不是很高的应用领域，从节省材料和性能兼顾的角度，也可以考虑使用梯形筋板结构的镁合金型材。

2 镁合金型材振动实验分析

2.1 实验过程及测试方法

2.1.1 实验材料

为了验证上述模拟结果，并且体现镁合金型材减振性能的优越性，实验选用一次挤压成形的AZ31镁合金型材编号1，2以及一次挤压成形的铝型材6N01编号3，进行对比实验。试件固定及加速度计安装情况如图4所示。

图4 试件固定及加速度计安装情况（a）1号、3号试件；（b）2号试件Fig.4 Specimen of fixed and accelerometer installation（a）sample of No.1 and No.3；（b）sample of No.2

2.1.2 实验方法

实验采用ACT2000－R0320S三向电磁振动台、GF0600K功率放大器、数字振动控制器、加速度计及相关的采集设备进行振动实验。用夹具将试件固定在三向振动台台面上，三向电磁振动台作为激振源，向试件提供加速度为29.41995m·s－2的激励。在10～450Hz的频率范围内，分别对试件进行水平（X向、Y向）、垂直（Z向）方向上速度为1个倍频的扫频振动。作为激励响应信号的采集，加速度计分别粘贴在两个比较有代表性的位置——试件的壁板中部和中间筋板中部，具体位置如图4所示。对同一载荷激励下，不同试件的加速度响应函数进行测试，并进行下一步数据的处理和分析。

2.2 实验结果分析及讨论

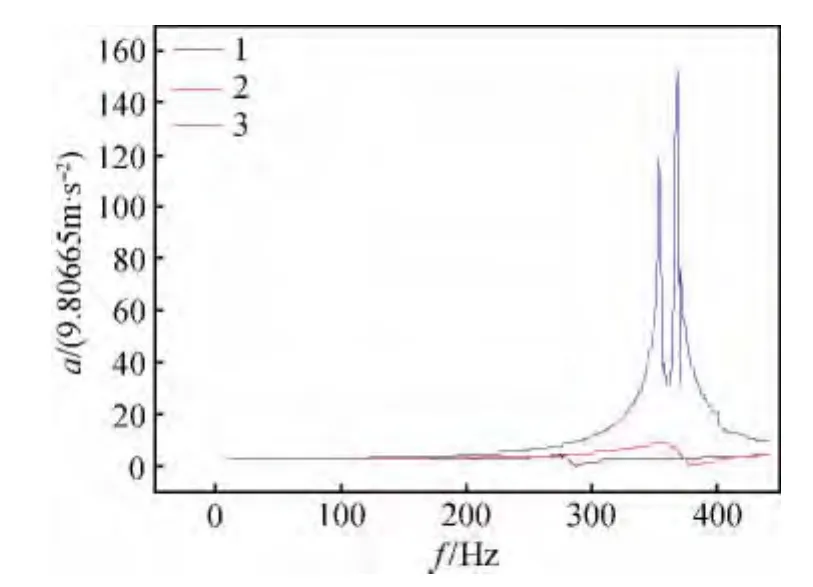
图5 各样品Z向振动对比Fig.5 Vibration of models in the Z direction

对于壁板而言，三个试件的响应加速度在Z向最为明显，因此取Z向的加速度响应曲线作分析。图5为1，2，3号试件垂直方向上壁板的加速度响应图，可以看出，在10～450 Hz频率范围内，3号试件（铝合金）的振动响应最为明显，有较多较高的谐振峰，其最大加速度达到1493.08156m·s－2，对应的最大位移也高达0.433659cm（表2）。1，2号试件（镁合金）的振动加速度响应曲线较为平缓，谐振峰较少。可见相同激励下，镁合金型材的振动比铝合金型材小得多。镁合金作为一种新型的材料在替代铝合金方面具有巨大的优势。另一方面，在0～450 Hz频率范围内，1号试件的加速度响应小于2号试件。各试件筋板处响应的最大加速度由表2可知：2＞1＞3，最大位移2＞3＞1。比较1号和3号试件，可得相同形状不同材料试件筋板处的振动情况：铝合金大于镁合金。比较1号、2号试件可知，相同材料不同形状试件筋板处的振动情况：矩形筋板型材振动大于三角形筋板振动。

总体而言，相同载荷激励下1号试件的振动响应比2号试件的振动响应小。对镁合金型材而言，三角筋板的布置方式优于矩形筋板的布置方式，这与之前模拟计算的结论一致。

表2 不同形状镁合金与铝合金加速度、位移响应表Table 2 Acceleration and displacement responses of different shapes magnesium and aluminum alloys profile

3 矩形筋板镁合金型材的优化改进

3.1 优化模型的建立

上述模拟和实验得出：相同载荷激励下，矩形筋板布置的镁合金型材整体变形较大。现针对这个问题，对矩形筋板布置的镁合金型材进行改进、优化。由于倾斜筋板的添加可以缓解应力，改善型材的整体变形情况，所以考虑在矩形筋板的基础上进行改进的两种优化方案模型如图6所示。按照1.1节中的方式设置模型相关参数，进行建模计算。

图6 矩形筋板布设镁合金型材优化方案（a）优化方案1；（b）优化方案2Fig.6 The optimized schemes of magnesium alloys with rectangular reinforcing plate （a）scheme 1；（b）scheme 2

3.2 计算结果与分析

对优化方案和原矩形模型前0.4s的应力、位移计算结果作对比分析，如表3所示，优化方案和原模型的受力情况为：有载荷作用时，除方案1在t＝0.10s时刻受力比原模型大以外，其余时刻，经过优化的模型所受应力有明显减小。外载荷消失后，方案2在有的时刻点存在应力比原模型略大的情况，方案1受力比原模型小。选择优化方案和原模型受力最大时刻的云纹图（图7）对比，优化方案减少了垂直筋板的数目，使得筋板与壁板的连接点减少，避免了一部分的应力集中，进而缩小了应力集中的范围。

对比两者的位移情况，无论是有载还是无载情况，两个优化方案的位移都比原模型小（表3）。选择各模型初始状态与最大变形（t＝0.10s）处的纵向截面作对比，图8为它们的位移云图对照图，可见最大变形位置都为模型中部，两种优化方案的镁合金型材整体变形比原矩形模型小，方案2中最大位移减小到9.35635mm，方案1中最大位移减小到6.55081mm，接近原模型最大位移的1／2。

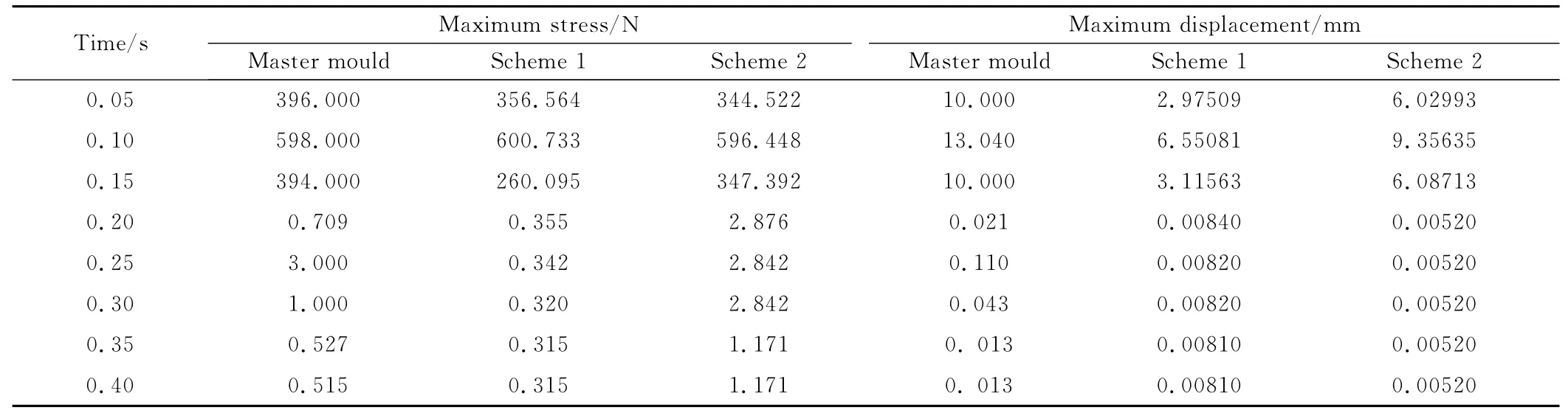
表3 优化方案和原模型0.4s内应力与位移对比表Table 3 Results of stress and displacement of the optimized and original model in 0.4s

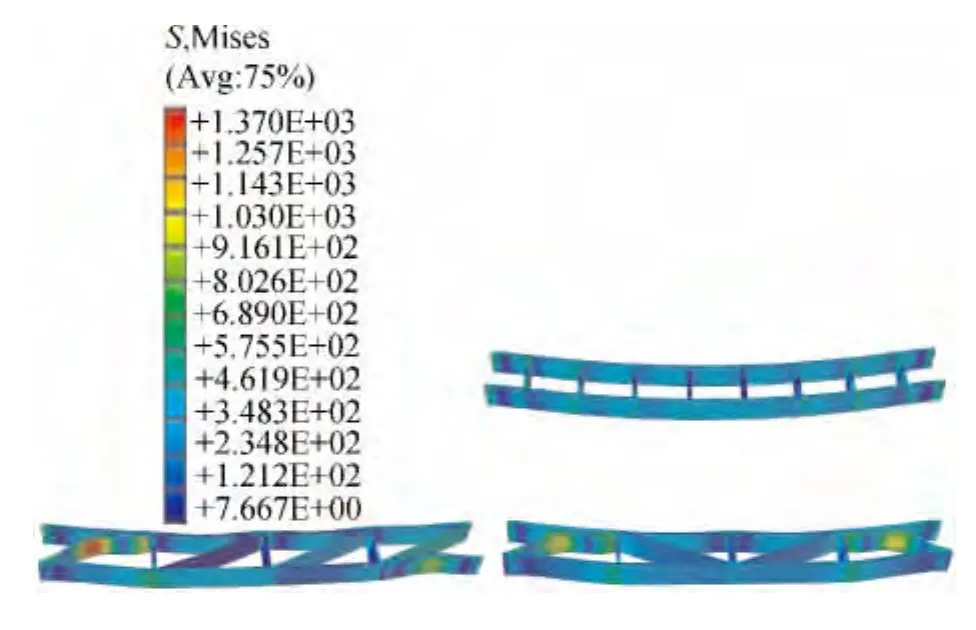
图7 优化方案和原模型最大应力时刻的云纹图Fig.7 Stress moire diagram of optimized and original models in the maximum deformation

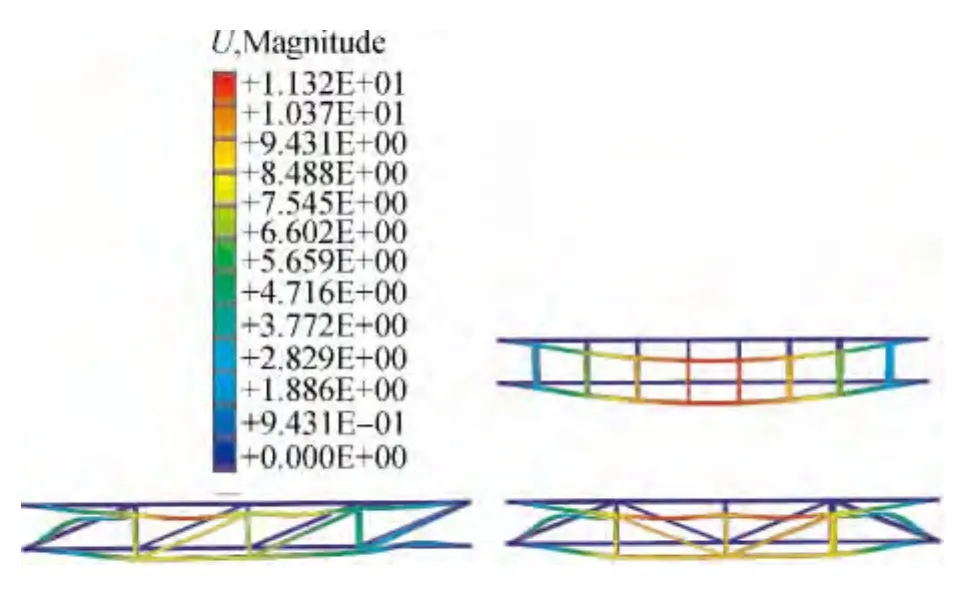
图8 优化方案和原模型最大位移时刻的云纹图Fig.8 Displacement moire diagram of optimized and original models in the maximum deformation

两种对矩形筋板的镁合金型材优化方案，在最大应力、位移和整体变形上都使得型材的性能有所改善。整体上看，方案1的改进优于方案2。

4 结论

（1）相同载荷激励下，三角形筋板的镁合金型材的振动性能要优于其他形状筋板布置的型材。

（2）镁合金型材振动性能优于铝合金型材。相同材料的镁合金型材，三角筋板较矩形筋板而言具有更好的优势，这与模拟结果相符合。

（3）对于矩形筋板的镁合金型材可通过在其间添加倾斜的筋板构成稳定的三角结构来达到减小整体型材变形、应力和位移的目的。

［1］ 李沛勇，戴圣龙，刘大博，等.材料阻尼及阻尼合金的研究现状［J］.材料工程，1999，（8）：44－48.

LI Pei－yong，DAI Sheng－long，LIU Da－bo，et al.Status of research on material damping and damping alloys［J］.Journal of Materials Engineering，1999，（8）：44－48.

［2］ 杨志康.基于铝合金型材的高速列车声学特性理论分析与研究［D］.哈尔滨：哈尔滨工业大学，2010.

［3］ 孙庆鸿，张启军，姚慧珠，等.振动与噪声的阻尼控制［M］.北京：机械工业出版社，1992.1－60.

［4］ ZHANG X N.Effect of reinforcements on damping capacity of pure magnesium［J］.Journal of Materials Science Letters，2003，22（7）：503－505.

［5］ NISHIYAMA N，ASANO S.Evaluation of amplitude dependence of internal friction in high－damping metals［J］.Journal of the Japan Institute of Metals，2001，65（2）：109－114.

［6］ GOKEN J，RIEHEMANN W.Damping behavior of AZ91 magnesium alloy with cracks［J］.Mater Sci Eng A，2004，370（1－2）：417－421.

［7］ WAN D，WANG J，LIN L.Damping properties of Mg－Ca binary alloys［J］.Physica B：Condensed Matter，2008，403（13－16）：2438－2442.

［8］ 张津，陶艳玲，孙智富，等.镁合金 AZ91D的阻尼减震性能［J］.机械工程学报，2006，42（10）：186－189.

ZHANG Jin，TAO Yan－ling，SUN Zhi－fu，et al.Vibration damping capacity of AZ91D magnesium alloys［J］.Chinese Journal of Mechanical Engineering，2006，42（10）：186－189.

［9］ 刘楚明，纪仁峰，周海涛，等.镁及镁合金阻尼特性的研究进展［J］.中国有色金属学报，2005，15（9）：1319－1325.

LIU Chu－ming，JI Ren－feng，ZHOU Hai－tao，et al.Research and development progress of damping capacity of magnesium and magnesium alloys［J］.The Chinese Journal of Nonferrous Metals，2005，15（9）：1319－1325.

［10］ PANTELAKIS S G，ALEXOPOULOS N D，CHAMOS A N.Mechanical performance evaluation of cast magnesium alloys for automotive and aeronautical applications［J］.J Eng Mater Technol，2007，129（3）：422－430.

［11］ SONG G.Recent progress in corrosion and protection of magnesium alloys［J］.Advanced Engineering Materials，2005，7（7）：563－586.

［12］ BENEDYK J C.Magnesium advances in automotive applications［J］.Light Metal Age，2005，63（3）：36－38.

［13］ POWELL B P.Magnesium alloys cast into auto powertrain components［J］.Advanced Materials and Processes，2004，162（8）：60－61.

［14］ 曾荣昌，柯伟，徐永波，等.Mg合金的最新发展及应用前景［J］.金属学报，2001，37（7）：673－685.

ZENG Rong－chang，KE Wei，XU Yong－bo，et al.Recent development and application of magnesium alloys［J］.Acta Metallurgica Sinica，2001，37（7）：673－685.

［15］ 高云凯，程金山，于会涛.镁合金轿车顶盖横梁结构设计与分析［J］.汽车技术，2008，（4）：9－13.GAO Yun－kai，CHENG Jin－shan，YU Hui－tao.Structure design and analysis of magnesium－alloy car roof members［J］.Automobile Technology，2008，（4）：9－13.

［16］ 张力，赵振奇，张丁非，等.AZ91D和A380合金模态参数识别和激励响应测试［J］.中国有色金属学报，2009，19（1）：44－49.

ZHANG Li，ZHAO Zhen－qi，ZHANG Ding－fei，et al.Modal parameter identification and vibration response testing of AZ91D and A380 alloys［J］.The Chinese Journal of Nonferrous Metals，2009，19（1），44－49.