基于OTA和CCCII实现的n阶多功能滤波器
曾菊员
(罗定职业技术学院电子信息系,广东罗定 527200)
0 引言
近年来,连续时间滤波器的研究受到了电路与系统学界的高度重视,并在通信、信号与信息处理及计算机外围设备等领域得到成功地应用[1~6]。运算跨导放大器(OTA)和多端输出的电流控制第二代电流传输器(CCCII)作为电流模式电路中的基本有源器件,具有很强的通用性和灵活性,它们已经成为电流模式电路中最基本的模块。
基于OTA与CCCII的二阶滤波器的设计已经比较成熟,已见一些典型电路,但是由OTA和CCCII结合起来实现的高阶滤波器目前还未见介绍。
本文基于迈逊信号流图理论,讨论了n阶滤波器的信号流图设计方法,设计出了一种新颖的基于OTA和CCCII的n阶多功能滤波器,它具有良好高频特性。
该多功能滤波器采用多重反馈的结构形式,其电路结构比较简单。它由一个CCCII,n个OTA和电容共同构成。我们改变反馈的级数就可以实现任意阶的电流模式滤波。
1 n阶多功能滤波器的分析与设计

由上式可得实现传递函数的信号流图,如图1所示。在信号流图中,共包括n个积分器,可用理想积分器实现,各输入变量与各积分器输出信号的相加可用形式加法器实现。
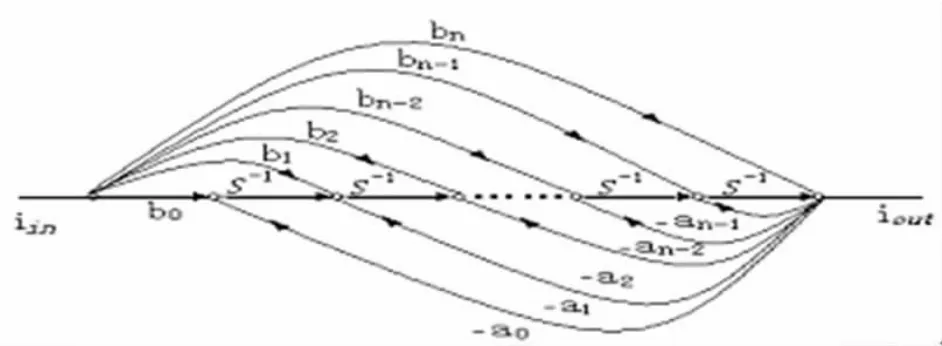
图1 式(2)的信号流图
根据图1得到实现函数式(2)的多功能滤波器由OTA积分器和CCCII加法器组成。如图2(a)所示的积分器传递函数为Io/Ii=G/SC。能实现求和功能的如图2(b)所示加法器传递函数为Io=Ii1+Ii2。

图2 多功能滤波器组成单元电路
根据信号流图,运用上述的积分器及加法器便可实现n阶基于OTA及CCCII的电流模式多功能滤波器,如图3所示。
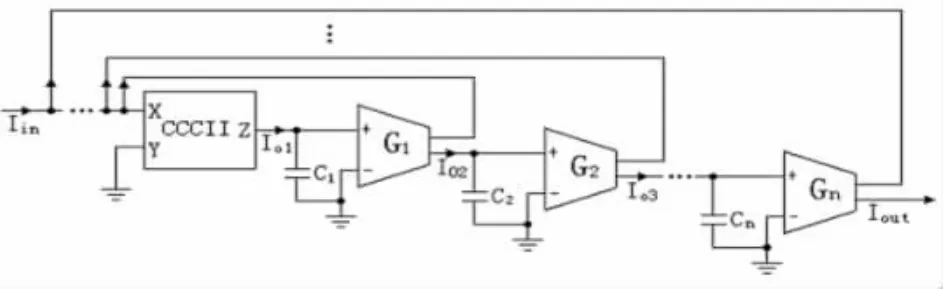
图3 n阶基于OTA及CCCII的电流模式多功能滤波器
图中,C1~n为积分器输入端外接电容,G1~n为OTA积分器的增益。
在图3中,根据OTA及CCCII的端口特性有
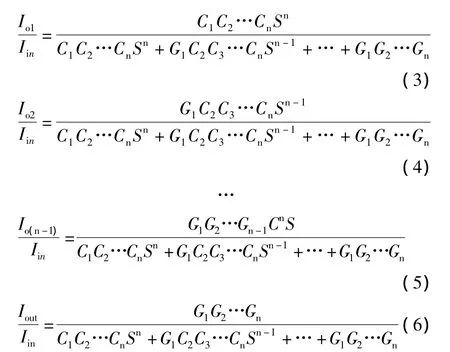
可以看出:式(3)可以实现高通滤波器功能,式(6)可以实现低通滤波器功能,式(4)~式(5)中任意一个式子都可以实现带通滤波器功能。若将式(3)与式(6)相加可得

2 设计举例
根据上述分析过程,我们可以设计一个四阶巴特沃思低通滤波器,如图4所示。
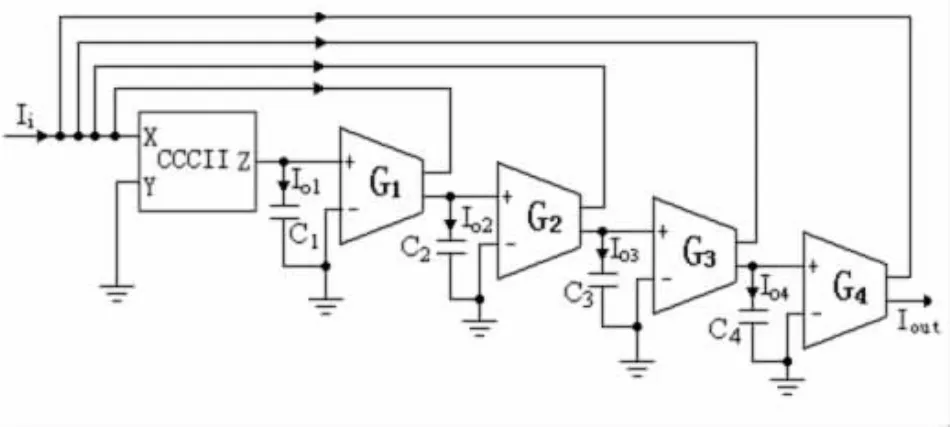
图4 四阶巴特沃斯低通滤波器原理图
四阶巴特沃斯低通LP、带通BP、高通HP和带阻BS滤波器的传递函数H(S)分别为


图5 OTA的实现电路
CCCII采用图6所示的电路。基于OTA和CCCII实现的四阶多功能滤波器频率响应特性实验仿真结果如图7所示。由图可见,仿真结果与理论分析完全一致,从而表明了本文所提出的电路设计方案的正确性。

图6 CCCII的实现电路

图7 四阶多功能滤波器幅频响应
3 结语
本文基于迈逊信号流图理论,讨论了n阶多功能滤波器的信号流图设计方法,成功地设计出了一种新颖的基于OTA和CCCII-实现的n阶多功能滤波器电路模型。该电路具有以下优点:
(1)设计方法简单明了,综合性强。无需改变电路结构,便可方便实现n阶低通、高通、带通、带阻以及全通五种基本功能的滤波电路。
(2)电路中不用电阻元件,且所有的电容元件都接地,有利于电路集成;
(3)无源灵敏度低;
(4)所设计的滤波器具有良好的高频性能。
[1]周细凤,曾荣周.基于OTA和CCCII的电流模式可调谐滤波器[J].北京,计算机工程与应用,2013,49(7):68~71.
[2]金丰,江金光.基于CCCII与OTA的三输入单输出多功能电流模式滤波器[J].西安,现代电子技术,2009,294(7):86~88.
[3]余国义,钟建福,张乐.适用于OTA-C滤波器的高线性OTA的设计[J].武汉,华中科技大学学报:(自然科学版),2013,41(4):60~64.
[4]杨鹏,刘桂芝,杨虹.用于红外接收芯片的OTA-C带通滤波器[J].成都,电子元件与材料:,2009,28(2):32~34.
[5]魏镜,王卫东.一种可编程高线性CMOS OTA的设计[J].南京,电子器件,2011,34(8):415~418.
[6]周德福,张勇虎.可变带宽 OTA-C连续时间低通滤波器设计[J].西安,现代电子技术,2011,34(6):157~159.

