关于“电路理论”课程的若干教学实践

陈希有，李冠林，周惠巍

(大连理工大学电子信息与电气工程学部，辽宁大连 116023)

“电路理论”课程的地位、作用和性质，决定了本课程教学中要始终探索教学内容与教学方法，以使学生具备扎实的电路理论基础和较强的工程意识，并在学习中养成良好的悟性和浓厚的兴趣。为此，笔者在教学第一线开展了相关的教学实践，籍此与读者交流。

1 关于课程绪论

绪论是教学的重要序幕，善始方能善成，其意义不言而喻。在教学中，把人们对电磁技术的认识过程进行梳理，按照从无意识观察到有意识探索;从定性研究到定量研究;从分散研究到系统归纳，给电磁规律发现的诸多历史事件以故事的形式来讲授。这样可以引导学生站在发展的角度看待这些历史事件所起的重要作用和彼此之间的递进关系，并由此对前辈的贡献产生由衷的敬仰之情。

麦克斯韦因为具备扎实的数学基础，所以统一了电磁光，完成了物理学的伟大综合，并预言了电磁波。法拉第由于数学基础不如麦克斯韦，虽然提出了场的概念，却没能完成电磁光的统一。以此故事强调学好数学的重要性，哪怕暂时不知道所学内容在将来会有何用途;库仑受牛顿万有引力定律启发，提出了点电荷之间的作用力公式，即库仑定律，将牛顿的力学原理扩展到电学与磁学中;欧姆受傅里叶研究热传导得出的热流量与温度差成正比的结论启发，提出了电阻上电流与电压的正比关系，即欧姆定律。我们以这些故事强调借鉴已有科学成果的重要性;爱迪生忙于商业运作，虽然首先发现了爱迪生效应，却没能首先发明电子管。以此故事强调持续研究、基础研究和科学敏锐性的重要性。

绪论课上，在总结电磁发展规律、阐明电的重要性和电路理论在当代科学与技术中所起的基础作用之后，便可顺理成章地阐述课程地位、课程性质、教学目的、教学内容和学习方法。

2 关于电磁学原理的运用

2.1 关于基尔霍夫定律

基尔霍夫定律是电路理论的基本定律，是关于电流和电压的定律，但它们并不能用于任何实际电路。因此需要透彻理解定律的正确性及其适用条件，以便在遇到工程实际问题时，能够明辨是否可以使用这些定律。可分如下三个步骤加以阐明。

(1)电流与电压—定律的阐述对象

我们阐明自然界中存在着传导电流、运流电流和位移电流之分，因为这些电流都可能或多或少地存在于实际电路中，而“电路理论”只涉及传导电流。与此并行的是自然界中存在着库仑电场、感生电场和局外电场，这些电场也都或多或少地存在于实际电路中，而“电路理论”专门研究库仑电场的做功情况，并用端电压(简称电压)作为变量。

(2)集中参数电路—定律的适用条件

前面提及位移电流和感生电场的概念，它们可以用来从电磁学角度阐述集中参数电路:不计元件以外的位移电流，可用电容元件来表示;不计元件以外的感生电场，可用电感元件来表示;不计导线分布的电阻和漏导，可用集中的电阻和电导来表示。

为了不计上述位移电流和感生电场，要求电路中的电流和电压满足变化不是很快的条件，即在电磁波传遍整个电路的时间内，不能明显地觉察到电流或电压的变化。相当于电路的最大尺度远小于最短电磁波波长。

为了不计导线分布的电阻和漏导，要求满足线路不是很长的条件。当线路电阻电压没有明显改变线路两端的电压，并且线路的漏导电流没有明显改变线上的传导电流，就意味着线路不是很长。

集中参数电路是同时满足变化不是很快和线路不是很长的电路，是一种理想化的电路模型。

(3)运用电磁学原理阐明基尔霍夫定律—定律的正确性

在集中参数电路假设下，用全电流连续性定律便可证得KCL。如图1和下式所示。

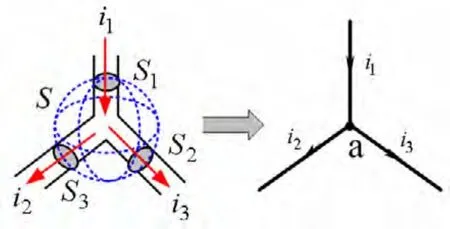
图1 基尔霍夫电流定律说明

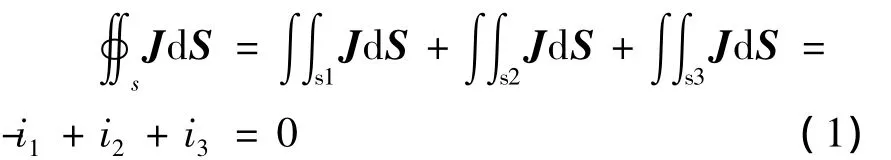
式中，J表示导体内电流密度矢量。

在集中参数电路假设下，用库仑电场的性质便可证得KVL，如图2和下式所示。

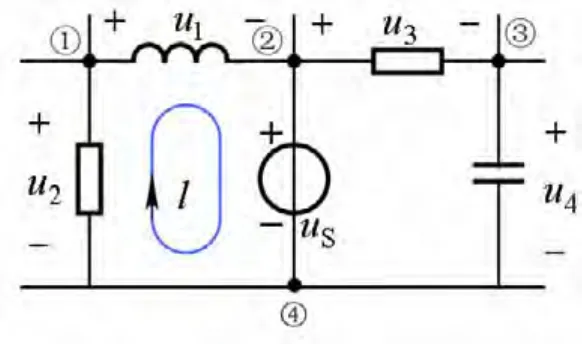
图2 基尔霍夫电压定律说明

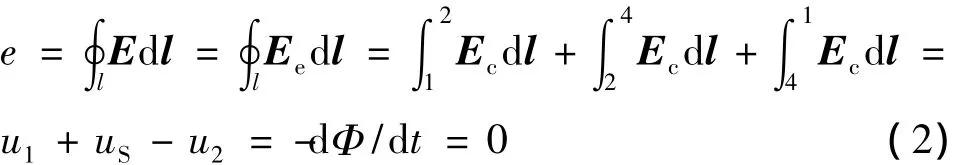
上式中的E表示总电场强度，Ee表示库仑电场强度，Φ表示穿过闭合积分回路l的磁通。我们可以从上述过程更好地理解KCL和KVL所需要的假设条件。

2.2 关于均匀传输线方程

用位移电流和感生电场的概念建立均匀传输线方程，可使两个方程和谐对称，不会出现只在一个方程中忽略二阶无穷小的现象。用图3(a)建立电压方程，如式(3);用图3(b)建立电流方程，如式(4)。这两个方程结构对称。当微段长度Δx→0时，便成为形式优美的均匀线方程，如式(5)。式中R0，L0，G0，C0分别表示均匀线单位长度的电阻、电感、电导和电容。

图3 均匀线方程的建立

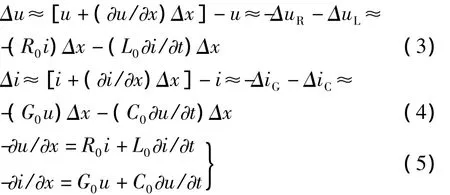
2.3 关于理想变压器

理想变压器常用在磁耦合器件例如铁心变压器的模型中，所以宜从图4所示的实际变压器出发，通过假设来建立理想变压器模型，由此可以分别得出电压变换和电流变换所需要的不同假设条件。

图4 铁心变压器示意图

由此可见，电动势或电压变换关系的存在，与磁导率大小和是否存在涡流损耗无关。

电流变换关系的主要依据是安培环路定律:

若磁导率为无限大，则H=B/μ=0。上式等号左边积分等于零;若不计涡流，则上式等号右边只包含线圈电流，而不包含铁心涡流。在这两个条件下，便存在电流变换关系:

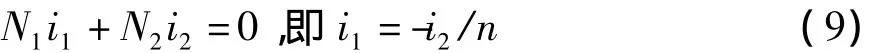
由此可见，电流变换关系与是否为全耦合和是否存在导线电阻损耗无关。

若满足全耦合、磁导率为无限大、不计导线损耗与铁心损耗的条件，则电压变换与电流变换关系便同时成立，得到理想变压器模型。之所以区分电压变换和电流变换所需要的条件，是因为这两个变换关系在工程上有时会单独使用。

3 关于数学方法的运用

电路理论除用电磁学原理来阐释外，还可用数学方法加以证明。我们采用了如下的教学实践。

(1)基于互感储能Wm非负的客观事实和半正定二次型的性质，可证明耦合系数小于1的结论:

(2)基于线性方程组的可加性建立叠加定理，自然说明了叠加定理的应用条件和应用方法［3］。

(3)将正弦量的相量表示建立在数学变换基础上，以期减少相量等于正弦量的常见错误，并与后面的拉普拉斯变换作如下呼应:

利用相量变换的性质，建立KCL、KVL和元件方程的相量形式，其过程严密，符合电路变换域分析的一般原理。

(4)将全响应等于零输入响应与零状态响应相叠加的结论，建立在线性微分方程解的可加性基础上［4］。例如对RC电路有

诸如上述数学方法的运用，一方面可以使得电路理论的叙述更加严密，另一方面有助于引导学生面对工程问题时，学会使用数学方法进行理性思维，并注重对后续数学课程的学习。

4 关于概念与方法

电路理论是概念与方法的集合。为强调“电路理论”课程中基本概念的重要性，教学时采用如下方法:①按照做功→消耗或储存能量→做功速率即功率的物理顺序，介绍电阻、电容和电感元件的能量特性和功率计算;②在阐述回路电流法和节点电压法时，主张直接根据基尔霍夫定律列写方程。这样，方程中每一项都对应具体元件的电压或电流，遇到诸如纯电流源、纯电压源支路，以及运算放大器和理想变压器时也知道如何列写电路方程，以免机械地使用自阻、互阻或自导和互导的规则所导致的列写错误;③在阐述戴维南定理时，从线性电路的性质入手，得出一端口网络电压与电流关系是一条直线，再通过分析这条直线得出戴维南等效电路，如图5和下式所示。

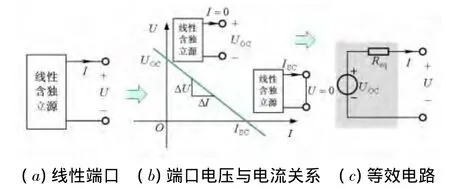
图5 根据电路性质得出戴维南定理

5 关于理论联系实际

在讲述某个理论内容的同时有意联系与之密切相关的实际问题，使理论与实践及时结合。例如:①在介绍实际器件主要电磁特性之后，简要介绍它们的额定值，以便正确应用这些器件;②总结实际电源与理想电源的差别;③在介绍运算放大器时，分析采用平衡电阻的必要性和有源滤波器不使用电感的原因;④通过分析RC充电效率低下的原因，提出提高充电效率的分段充电方法，如图6所示［5］。效率表达式为 η =we/w=2/(3+e－T/τ)，当T＞ (3 ～5)τ时，充电效率近似 :⑤对电弧、碳化硅陶瓷、晶体管、忆阻器以及电滞特性的非线性电容的介绍，使抽象的非线性元件有了具体的工程背景。

图6 提高效率的分段式RC充电电路

6 关于拓展内容

在教学实践中，为学生准备一些拓展内容是必要的，这些拓展内容是基本内容的自然延伸。例如:①介绍基尔霍夫的最初论文，以使学生了解基尔霍夫定律与当年基尔霍夫论文的关系，并对基尔霍夫本人产生敬仰之情;②以参数变动电路的计算为示例，介绍置换定理的特殊应用;③通过对灵敏度的简单分析，为特勒根第二定理和互易定理找到特有的应用场所;④利用互感储能是电流状态单值函数的概念，证明两个互感系数相等的结论;⑤结合中性点位移的概念，详细分析了相序指示器原理，并启发学生针对存在的问题提出改进措施;⑥在双绕组变压器基础上，分别介绍三绕组变压器、带中心抽头变压器和自耦变压器，这些都是实践中常用的变压器;⑦通过对忆阻器的介绍，使教学能够及时反映电路元件的最新研究进展。

7 结语

以上简要介绍了笔者在“电路理论”课程中的若干教学实践，关于上述教学实践的详细内容，以及其他教学实践参见文献［6］。这种教学实践是因材施教性的，需结合具体教学对象加以实施。本文已在“高校电子电气课程教学系列报告会(2013)”上宣读。

［1］俞大光.电工基础(修订本)［M］.，上，中册.北京:人民教育出版社，1964，1965.

［2］捷米尔强等编著，赵伟，肖曦，王玉祥等译.电工理论基础(第四版)［M］.北京:高等教育出版社，2011年1月.

［3］陈希有，刘凤春，董维杰，李冠林.在电路教学中培养学生的数学应用能力［J］.南京:电气电子教学学报，2010，32(5):51－55.

［4］陈希有，刘凤春，李冠林，董维杰.线性动态电路暂态过程全响应可加性的教学方法［J］.北京:中国电力教育，2010，(6):100－102.

［5］陈希有，李冠林，刘凤春.RC电路充电效率分析［J］.南京:电气电子教学学报，2012，34(2):32－35.

［6］陈希有.电路理论教程［M］.北京:高等教育出版社，2013年8月.