含运算放大器的一阶电路时间常数的计算

赵艾萍，张 峰

(上海交通大学电子信息与电气工程学院，上海 200240)

在电路教学中，经常会讨论一阶动态电路的时间常数［1、2］。这是因为时间常数不仅是反映一阶电路特性的关键参数，更是应用三要素法求解一阶电路的关键要素。但笔者在教学中发现，很多学生遇到含运算放大器的一阶电路时，经常手足无措。针对这一情况，本文选取含运放的一阶电路的三种典型情况，详细介绍求解其时间常数的三种方法:经典法、外加电源法和等效变换法。本文试图通过这些计算方式让学生正确理解和掌握多种分析计算方法，并最终达到熟练使用等效变换简化计算的目的。

现在，本文以图1为例，讨论求解一阶动态电路时间常数的方法。

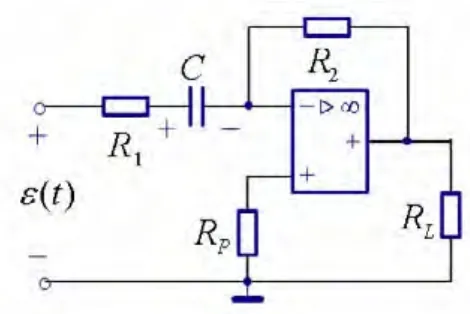
图1 C在输入端的含运放的一阶电路

1 经典法

根据理想运算放大器的虚短和虚断特性，可知有u－=u+=0V。进而可以给出输入回路方程:

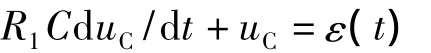
根据其特征方程，可求得时间常数为R1C。

2 外加电源法

一阶电路的时间常数的计算关键是求从储能元件两端看进去的电路的戴维南等效电阻［2］。本例具体做法是先将内部独立电压源短路，然后将电容替换成独立电压源Uo如图2所示，最后计算Uo与Io之比即为等效电阻。

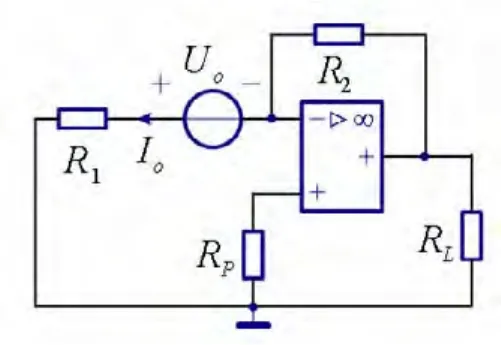
图2 图1电路外加电源求等效电阻

根据理想运放的虚短和虚断特性，同样可知u－=u+=0V，所以Uo=R1Io。故等效电阻是R1，可得此电路时间常数为R1C。

3 等效变换

在计算含运放的一阶电路时间常数的时候，笔者指导学生采用一种更加简化的等效手段:等电位点之间短路，零电流支路开路。下面以图1电路为例简要说明。

因为虚断特性，可将运放的两条零电流输入支路断开，如图3所示。

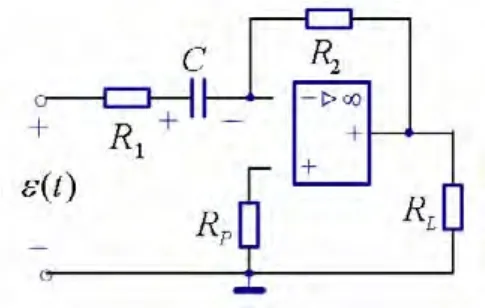
图3 图1电路的零电流支路开路

Rp电阻支路零电流，所以其两端压降为零，又因为虚短特性，可得u－=u+=0V。所以我们可将反相端与参考点之间短路，如图4所示。

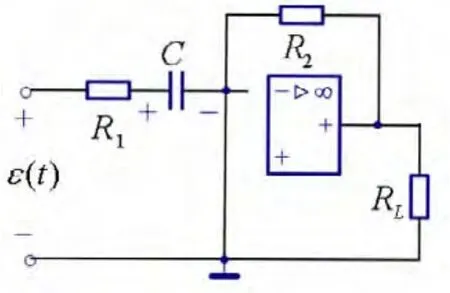
图4 图1电路的等电位点之间短路

此时，从电容看进去的戴维南等效电阻就是R1，从而也就轻易求得此电路的时间常数为R1C。

4 两个含运放的电路例题

下面参照文献［1］中提到的含运放电路的另两种情况尝试用等效变换法简要说明解题过程。

［例1］求图5所示一阶电路的时间常数，此时电容C位于运放的输出端。

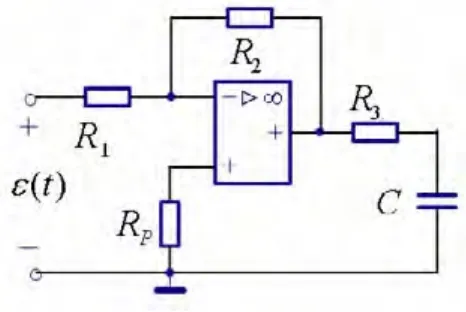
图5 C在输出端的含运放的一阶电路(例1)

因为虚断特性，可将运放的两条零电流输入支路断开。同样因为虚短特性，可得u－=u+=0V。如图6所示。

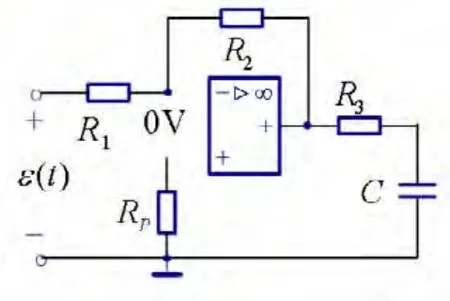
图6 例1电路的零电流支路开路

接着，计算从电容两端看进去的戴维南等效电阻。首先必须对内部独立电压源置零(即短路)，如图7所示。

图7 例1电路内部独立电源置零

由图7可知，电阻R1两端等电位，所以电阻R1为零电流支路，那么此时R2也为零电流支路且R2两端等电位。故运放输出端的电位与参考点相等，此时电路可以简化如图8所示。

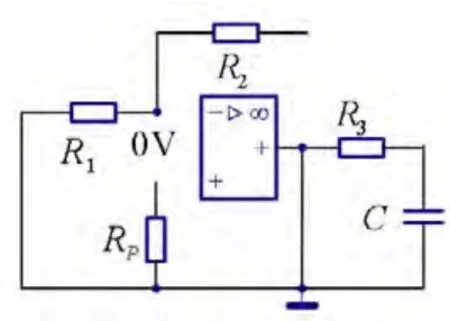
图8 例1电路的零电流支路开路

由此可见，从电容两端看进去的等效电阻为R3，时间常数为R3C。

［例2］求图9所示一阶电路的时间常数，此时电容位于运放的负反馈支路。

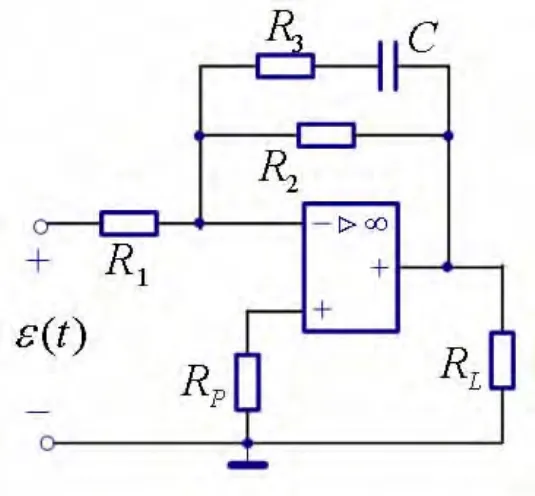
图9 C在反馈支路的含运放的一阶电路(例2)

同样，计算从电容两端看进去的等效电阻时，先置零独立电源。又因为虚短和虚断的特性，可知R1为零电流支路，将R1支路和运放反相输入端都开路，反馈支路接回输入端的这一侧支路上没有电流。根据广义KCL可知反馈支路接运放输出端的支路也为零电流支路。如图10中，被封闭曲线切割的两条支路零电流。将它们断开后，从电容看进去的等效电阻为R2+R3，故时间常数为(R2+R3)C。

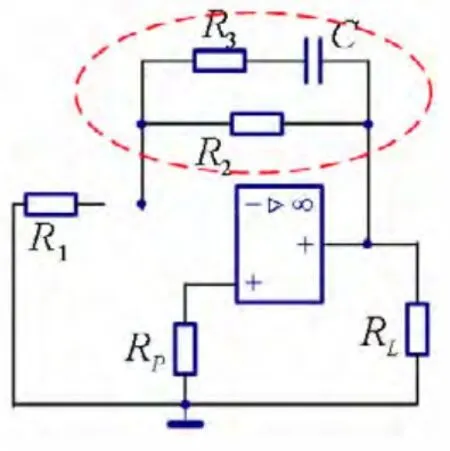
图10 例2电路的零电流支路开路

5 结语

含运放的一阶电路时间常数的计算一直是令学生困扰的问题。笔者在电路教学中通过三种计算手段循序渐进地加深学生对基本概念的理解和对基本方法的掌握。外加电源法与等效变换法的本质是相同的，但后者巧妙地利用零电流支路开路和等电位点之间短路化繁为简，更易于掌握。

［1］田社平，张峰.关于一阶电路时间常数求法的讨论［J］.南京:电气电子教学学报，2013，35(1):9-11

［2］陈洪亮，张峰，田社平.电路基础［M］.北京:高等教育出版社，2007