舰载舷外有源诱饵内外场综合试验方法
张鸿喜,韩 伟,张志辉
(解放军91404部队,秦皇岛 066001)
0 引 言
为有效防御反舰导弹的攻击,国内外十分重视发展舷外有源干扰技术,典型的装备有美海军的AN/SSQ-9(V)有源电子诱饵等。舷外有源干扰是利用悬停、拖曳、漂浮等布放方式对反舰导弹末制导系统实施干扰,该干扰技术的应用特点是降低了对防御平台的限制,可以综合配置干扰设备,使干扰方式多样化、灵活化、综合化[1]。但随着武器系统越来越复杂,造价越来越高,试验鉴定的难度也越来越大,试验中试验样本的费用和靶场的试验消耗也随之增大。因此,如何减少试验的样本量,节省试验经费,又不降低试验结果分析的精度或增加试验评估的风险,是研制方及军方极其关注并亟待解决的问题。舰载舷外有源诱饵试验也面临这样的问题。近年来在导弹、电子系统等试验鉴定领域应用比较活跃的小子样理论为解决问题提供了思路和手段[2]。本文以Bayes方法为理论基础,研究舰载舷外有源诱饵的内外场综合试验方法。
1 内外场试验方法简介
目前进行装备试验时可分为内场试验和外场试验两部分。内场试验主要是在微波暗室等室内环境中,运用仿真手段检验鉴定装备性能指标;外场试验则主要依托实装、模拟器等构设试验条件,在真实环境条件下进行。为更加充分、客观地检验装备的战技术性能,内外场试验手段是在一体化试验设计下相互补充、综合运用的。
1.1 数学仿真试验
数学仿真试验是以计算机为工具,根据试验目的,建立(实际的或设想的)全系统模型,并在不同条件下对模型进行动态试验的方法。数字仿真的主要特点是大样本、超实时,可利用数理统计学的方法分析系统变化的规律或所具有的性能。数学仿真试验克服了限制外场试验的一些制约条件,如敌方装备不充分或外场试验条件不能代表特定战场态势等等,并且可以很容易地根据战场态势修改信息,通过已知参数和其他场景中的真实数据来补充外场试验的结果。通过把真实试验测量结果归并到一定任务的数学仿真模型中,数学仿真试验还可以把试验结果外推到不能直接由外场试验来确定的效能指标上。
数学仿真试验也存在一定的局限性:试验结果的可信度与数学仿真模型直接相关。数学模型如果未经证实或认可,其结果可信度不够,即使数学模型得到了证实和认可,其结果也不可能得到像外场试验那样的可信度。因此数学仿真试验作为一种独立的试验手段,目前还不成熟,不完善。数学仿真试验适合于作为装备试验鉴定的辅助手段,可加强、扩展或充实内场半实物仿真试验和真实外场试验的结果[3]。
1.2 半实物仿真试验
半实物仿真试验主要在微波暗室内开展实施,有实际装备(部分)嵌入到试验系统中,通过硬件和软件来模拟装备所遭遇到的电磁环境。从电磁环境信号与被试装备的耦合方式来看,半实物仿真在实现方式上分辐射式(空间接收)和注入式2种。2种方式各有特点,辐射式能保证被试装备在试验过程中的完整性;而注入式,无论是射频注入还是中频注入,应用较为灵活、经济。
半实物仿真试验的优点主要有试验环境可控、过程可控、数据录取容易、重复性好、效费比高、保密性好等,但也有其局限性,主要在于试验结果的可信度与仿真模型直接相关,仿真模型的开发、检验和认可代价比较昂贵。
1.3 外场试验
外场试验是在真实的海洋环境、气象条件下,装载于实装舰或试验舰进行的试验,其试验环境逼真未来战场态势,能够获得可信度较高的试验结果。其中自然环境影响较大的试验项目、架设条件影响较大的试验项目、受战术使用方法影响较大的试验项目、与其他武器系统相关的试验项目等更适合外场试验。但外场试验也存在局限性,主要表现在试验成本高、组织指挥难、受天气影响大、周期长、成本高、试验保密性差、可重复性差、试验获得样本量小。
综合上述3种试验手段,从舰载舷外有源诱饵试验应用的角度分析,外场试验是在特定条件下,针对环境及装备的实际试验,能为舰载舷外有源诱饵性能和效能研究提供特定条件下可信的试验数据;半实物仿真试验是在可控的各种状态下进行重复性、探索性的仿真试验,能够对系统的某些性能指标提供验证和测试环境,可以获取大量的试验数据及其统计分析结果,为数学仿真提供可信的数据和模型支持;数学仿真试验用于工程级的试验鉴定,必须建立信号级仿真模型,开展基于信号流的仿真研究,较真实地反映传感器和干扰信号的对抗交互过程和对抗结果。通过信号级仿真试验可以检验舰载舷外有源诱饵性能指标,同时可获取大量的、可信的仿真数据,支撑其它试验手段不能实现的功能。
在实际试验应用中,3种试验手段都是按照试验要求获得数据的工具,要根据试验的总体设计,结合实际保障条件进行选择使用。
2 综合试验鉴定的总体思路
对于舰载舷外有源诱饵试验,由于样本容量与试验成本密切相关,出于装备的造价等因素考虑,总是期望能够在较小的样本容量之下进行。从统计学观点出发,就是如何统计一个较小的现场试验样本数,并在此样本数下,尽可能地充分利用其他有用信息,在保证结果可信的前提下,有效地进行武器装备的性能、效能评估。基于小子样的Bayes理论与方法的基本思想就是将验前信息和现场信息融合后综合进行统计推断,以弥补现场试验数据的不足[4]。因此,舷外有源诱饵内外场综合试验方法研究的基本思路是将内场仿真试验结果用于试验鉴定,希望能够充分利用仿真试验结果数据的验前信息,结合外场试验样本信息,运用Bayes小子样理论与方法完成对装备指标的评定与估计。
2.1 小子样统计理论
近年来,小子样理论研究已较为深入,取得了许多研究成果。小子样试验技术,特别是运用Bayes分析方法,可以充分利用多种验前信息,使试验的样本数明显地下降,受到国防科技研制、试验、使用部门的关注。
Bayes检验方法是基于总体信息、样本信息和验前信息进行的检验方法。它与经典检验方法的主要差异在于是否利用验前信息。Bayes方法有如下几个基本观点[5]:
(1)任何一个总体分布的未知分布参数θ都可以看做是一个随机变量,应该用一个概率分布去描述对θ的未知状况;
(2)分布参数θ具有验前分布π(θ),即在抽样试验之前就有关于θ的验前信息的概率分布;
(3)对应分布参数θ的任何统计推断,必须依据θ的验后分布来进行,这是因为在获得样本观察值之后,验后分布包含了对分布参数θ的全部信息。
在舰载舷外有源诱饵试验中,Bayes方法的应用包括两个方面:一是试验方案的设计,即保证决策风险尽可能小的情况下,尽量应用所有可能的信息(仿真试验、研制性试验等),设计在一定容量下,满足一定置信度的检验方案;二是根据仿真(研制性)试验数据提供的验前信息,结合外场试验数据提供的样本信息来对指标进行统计评估。
2.2 综合试验鉴定技术框架
舰载舷外有源诱饵的干扰成功率是一项概率性指标。考虑到在进行干扰效果试验时,每次试验有干扰成功和干扰失败2种结果,且每次试验结果互不影响。因此干扰成功率这个指标直观表现为成败型二项分布参数,对这个指标的评定可通过二项分布参数的评估与检验来完成。
2.2.1 试验方案设计
设定舰载舷外有源诱饵的干扰效果X服从二项分布,即X~b(n,p),利用二项分布Bayes假设检验进行方案设计[6]。
(1)首先进行统计假设
假设:

设P0为可接收的成功率,即干扰成功率的设计值,试验要加以验证;P1是P0的对立假设,是不可接收的成功率。
(2)计算验前概率
假设验前试验数为n0,验前干扰成功次数为s0,验前概率PH0(或π0)为:

式中:P(p0),P(p1)为 (n0,s0)以前阶段的验前概率,取P(p0)=P(p1)=50%,因此:
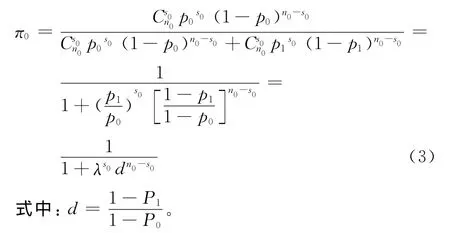
(3)确定试验样本数和试验成功数
记X= (x1,x2,…,xn)为独立同分布(i.i.d)子样,决策不等式为:

式中:Sn为试验结果成功数;n为试验样本数,π0为原假设H0的验前概率;π1为备择假设H1的验前概率。
贝叶斯假设检验的风险为:
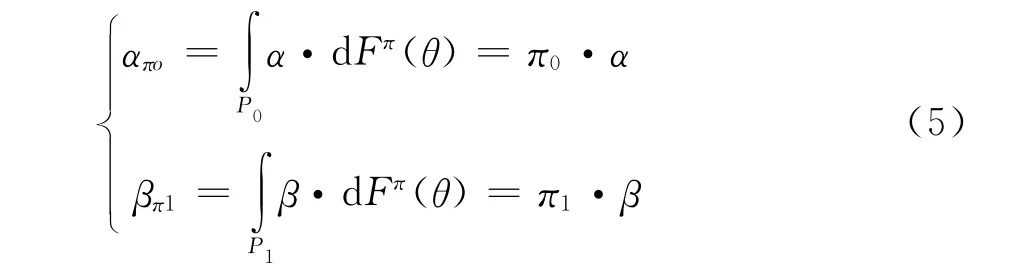
在应用中,要求风险απo,βπ1相当,并小于某一值。
2.2.2 干扰效果评定准则
以外场末制导雷达固定站试验条件下干扰效果评定为例,研究一般的评定准则。在这种试验条件下,一般是监测干扰前后以及干扰过程中末制导雷达输出的导引信号,主要是末制导雷达跟踪轴(电轴)相对于目标视轴(机械轴)的偏差,即跟踪误差(也称跟踪脱靶量)。设未实施干扰时末制导雷达的跟踪精度为σ(标准差),实施干扰后末制导雷达的跟踪脱靶量大小为θ,则可以依据以下标准判定对末制导雷达的干扰是否有效[7]:
(1)当θ≤3σ时,本次干扰无效;
(2)当θ>3σ时,本次干扰有效。
当然,上述准则使用时,还要考虑跟踪距离偏差和战斗指令等的变化进行综合判断。
由于干扰信号的存在,使得末制导雷达工作在具有随机性质的工作环境下,末制导雷达在干扰条件下的工作过程(特别是跟踪过程)是一个随机过程。在进行舷外雷达有源诱饵干扰成功试验时,采取以下的方式获取进行评估的数据样本:
(1)发射1枚诱饵弹,录取末制导雷达在有效干扰时间内的相关数据(航向电压、指令等),获得1个样本函数;
(2)对样本函数在各采样点的数据进行处理,根据相应评定准则判定为有效或无效;
(3)取样本函数的时间均值,对单枚诱饵弹成功与否进行判定;
当获得试验设计规定的样本数后,就可以对指标进行统计推断了。
2.2.3 试验信息处理和融合
统一评估准则后,要利用试验数据进行评定,但仿真试验数据必须可信,也即仿真试验的输出与外场试验的输出在统计意义上应该是一致的。最基本、最直接的方法是检验在相同的输入条件下仿真试验结果和外场试验结果之间是否一致以及一致性的程度如何。一般地,常用非参数检验方法。在工程应用中,常用 Wilcoxon-Mann-Whitney的秩和检验法。
在综合试验方法中,考虑Bayes方法在信息如何融合问题上,引入了可信度来描述不同来源信息[8],计算公式如下:

在多源验前信息下,可以由验前信息加权而获得关于θ的验前分布密度:
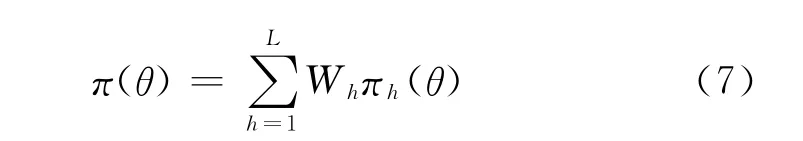
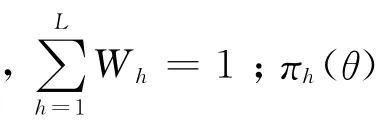
这样,当获得现场子样X之后,θ的验后密度为:
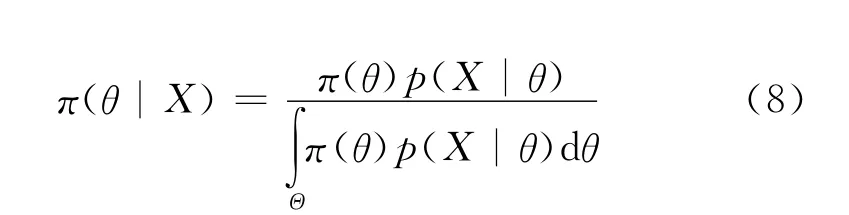
式中:Θ为θ的取值空间。

2.2.4 综合分析评定
综合评定涉及验前信息的综合,包括仿真试验和研制性试验信息。由于外场试验子样有限,采用仿真试验结果,在对仿真模型进行验证并对仿真试验结果和外场试验结果进行相容性检验后,进行数据混合,得到综合子样进行评定。这里将上述问题归结为Bayes统计推断问题,即用到Bayes点估计和区间估计理论,这里不再详述。
3 实例分析
在进行外场试验之前,采用半实物仿真和数字仿真手段分别对舰载舷外有源诱饵干扰成功率进行试验,得到试验结果如表1所示。

表1 仿真试验结果
3.1 试验方案设计
3.1.1 计算验前概率
经初步分析,X3与X2和X4相差较大,仅把X2和X4作为验前信息。首先计算X2和X4的可信度,即验前信息可信度,取P2(H0)=0.8,P4(H0)=0.5,弃真、纳伪概率都取0.2。则根据公式(6)计算可信度为:

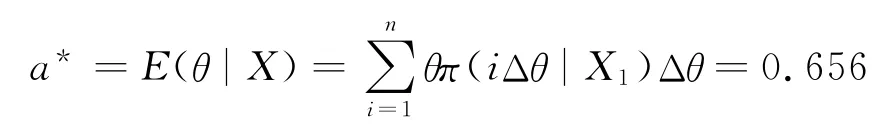

图1 融合后先验分布概率密度曲线
3.1.2 外场试验方案设计

根据上述内外场试验数据融合后的概率分布结果,进行Bayes点估计,θ的估计值a*近似计算为:
根据式(4)和式(5)计算可得如表2所示的Bayes检验方案。

表2_Bayes检验方案
试验前,要基于以上Bayes检验方案确定试验样本量。确定时既要考虑干扰成功概率指标的检验,还要考虑比如可靠性等指标检验的结合等。同时,试验样本量的确定还要考虑试验成本以及研制方和使用方风险,一般遵循研制方和使用方风险相当,或者使用方风险略低于研制方风险的原则。
3.2 结果分析评定
3.2.1 数据一致性检验
设获得外场试验数据为:X1=(1,0,1,1,0,1,1,1,0,1)。
把外场试验数据作为现场数据,采用秩和检验法进行与仿真试验数据的一致性判断。以外场试验数据为准,求出各仿真试验数据秩和,其中排列位置存在多种情况,则取各情况均值得:T2=192.5,T3=152.5,T4=447.5。取显著性水平α=0.5,通过查标准正态分布表可得uα/2=0.68,仿真试验数据与外场数据一致性必须满足以下条件:164.97≤T2≤ 225.03,164.97 ≤T3≤ 225.03,404.34≤T4≤495.62。所以,其中X3不满足一致性要求,摒弃不用。
3.2.2 综合分析与评定
根据公式(8)和(9),在3.1.1节的计算基础上,再次使用Bayes公式计算可得外场与仿真试验融合后的分布曲线,如图2所示。
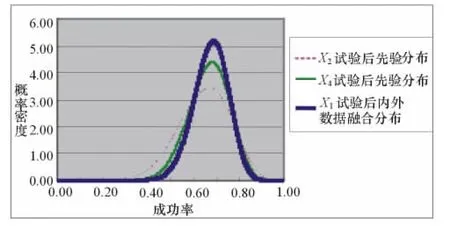
图2 内外场试验数据融合后分布概率密度曲线
则θ的Bayes点估计值a*计算为:

即干扰成功率为67.6%。θ的Bayes区间估计计算公式为:
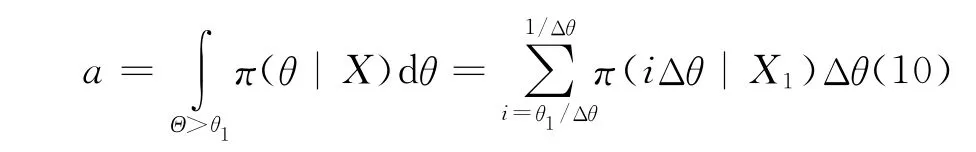
由式(10)可得:成功率大于60%时,置信水平为83.8%;成 功 率 大 于70% 时,置 信 水 平为39.1%。
4 结束语
本文针对舰载舷外有源诱饵的特点,提出了舰载舷外有源诱饵内外场综合试验方法。基于小子样的Bayes理论与方法,充分利用内场仿真试验结果,将内场仿真试验结果作为验前信息,进行外场试验设计,并将内场和外场试验数据进行融合处理,实现对装备性能、效能指标的全面评定。在具体试验实施中,还有许多内容需要进一步深入研究,比如评估样本的获得、各类数据可信度的计算、信息融合等。因此还需要进一步研究小子样试验方法,实现方法创新和应用可行,更好地促进舰载舷外有源诱饵综合试验鉴定技术发展。
[1] 许政,王强,于勇.舷外有源诱饵干扰作战使用研究[J].现代电子技术,2010(21):61-64.
[2] 唐雪梅,周伯昭,李荣.武器装备小子样综合试验设计与鉴定技术[J].战术导弹技术,2011(2):51-56.
[3] 王国玉,汪连栋.雷达电子战系统数学仿真与评估[M].北京:国防工业出版社,2004.
[4] 唐雪梅,宋春雳,李荣.多状态试验数据融合处理方法[J].战术导弹技术,2011(1):1-6.
[5] 王国玉,汪连栋,申绪涧,等.电子系统小子样试验理论方法[M].北京:国防工业出版社,2003.
[6] 曲宝忠,孙晓峰.海军战术导弹试验与鉴定[M].北京:国防工业出版社,2005.
[7] GJB 793A-2009.反舰导弹末制导雷达抗有源干扰陆上试验规程[S].
[8] 张金槐,刘琦,冯静.Bayes试验分析方法[M].长沙:国防科技大学出版社,2007.

