滚珠丝杠进给系统轴向接触刚度研究*

马 彦 李 威

(北京科技大学机械工程学院学院，北京100083)

近年来，精密机械的广泛应用对定位系统提出了更高的要求，而定位系统的主要功能部件就是丝杠进给系统［1-3］。丝杠进给系统是一种力和运动传输装置。丝杠进给系统最重要的两个特点是它的定位精度和承载能力［4-6］。这两个优点使它适合用作机床进给机构和高精密平台的驱动副［7-9］。滚珠丝杠进给系统已使用许多年了，但关于滚珠丝杠进给系统(以下简称统杠进给系统)性能参数(像轴向载荷、接触角、滚珠个数、螺旋升角和曲率比)如何影响丝杠进给系统的轴向接触刚度还没有彻底研究清楚。

1 赫兹点接触理论

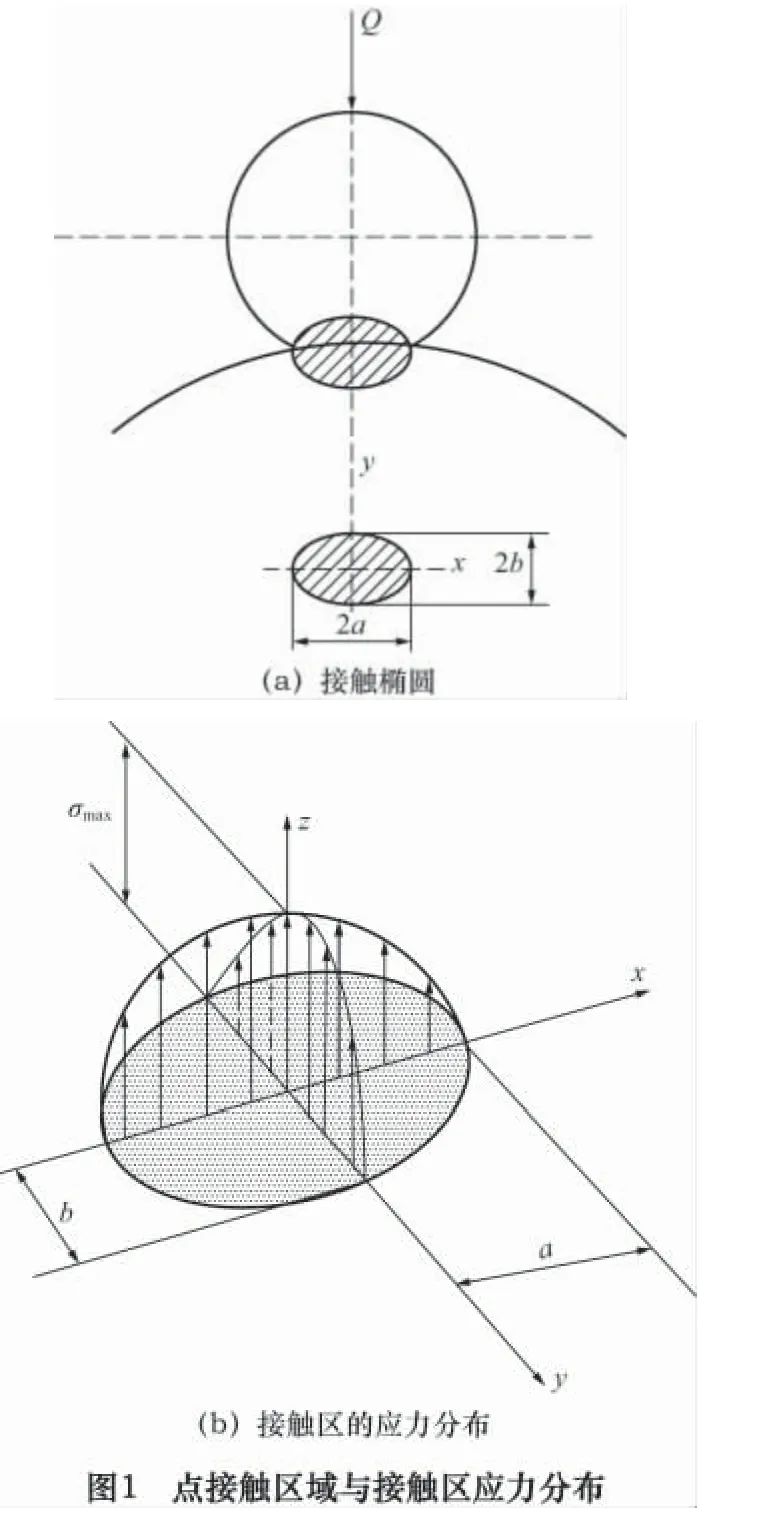
点接触的两个物体，在载荷Q的作用下，接触点将扩展成为一个接触面。该接触面在与接触法线垂直面的投影为一个椭圆，长轴为2a，短轴为2b，如图1a所示。在接触区域内，接触应力按半椭球分布，如图1b 所示。

根据赫兹接触理论，可推导整理出丝杠进给系统中滚珠与丝杠、螺母之间的接触椭圆尺寸、接触变形和接触应力之间关系的公式，分别为:

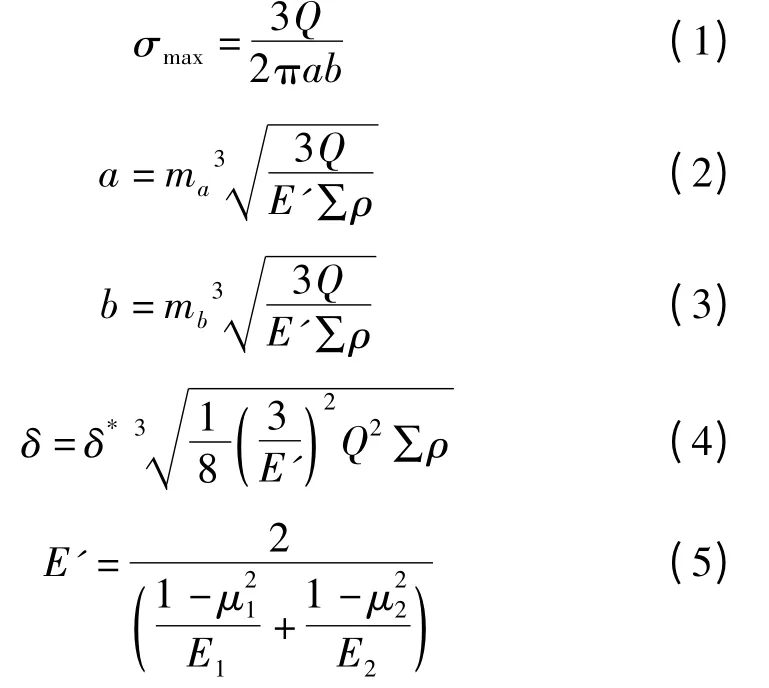
式中:Q为单个滚珠所承受的法向压力;a、b为接触椭圆长、短半轴;σmax为最大接触应力;δ为两接触物体上相距很远点之间的相互趋近量;E'为当量弹性模量;E1、E2为两接触物体的弹性模量;μ1、μ2为两接触物体的泊松比;∑ρ为两物体在接触点处的主曲率之和，仅与接触副的形状有关;ma、mb为接触椭圆的长、短半轴系数;δ*为仅与接触椭圆的椭圆参数有关的无量纲系数。

2 丝杠进给系统轴向接触刚度理论模型的建立

丝杠进给系统在轴向载荷的作用下，中间元件滚珠分别与螺母、丝杠滚道面接触，以传递载荷，并产生相应的接触变形。当滚珠与滚道面在载荷作用下相接触时，可以看作是两个自由曲面弹性体在压力作用下的点接触问题。丝杠进给系统的接触刚度来自于滚珠、丝杠和螺母弹性元件的弹性变形。该接触刚度指丝杠进给系统结合面在外力作用下抵抗变形的能力。一般以在加载方向上使丝杠进给系统产生变形量为1 μm 时所需要的力F来表示，即

式中:K为丝杠进给系统的接触刚度;F为丝杠进给系统的轴向载荷;ΔL为丝杠进给系统的轴向接触变形量。

根据赫兹接触理论，如果已知丝杠进给系统中钢球与滚道接触副的结构参数，就可以计算出丝杠进给系统中的接触压力和变形，进而求得接触刚度。

2.1 丝杠进给系统的轴向载荷Q

考虑螺旋升角，假设单个滚珠受到的法向载荷为Q，总体滚珠受到的法向载荷为Qz=zQ，则总体承载滚珠的法向载荷Qz和螺母受到的轴向推力Fa之间的关系为

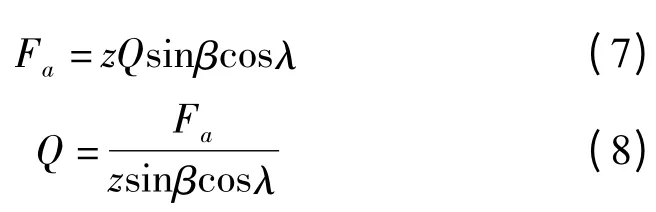
式中:Fa为螺母受到的轴向推力;z为总的工作滚珠个数;β为接触角;λ为螺旋升角。

2.2 丝杠进给系统的轴向接触刚度

假设丝杠进给系统所受的工作载荷分布均匀，则在法向载荷的作用下，螺母滚道面与丝杠滚道面间由于法向弹性接触变形所产生的弹性变形量δn为

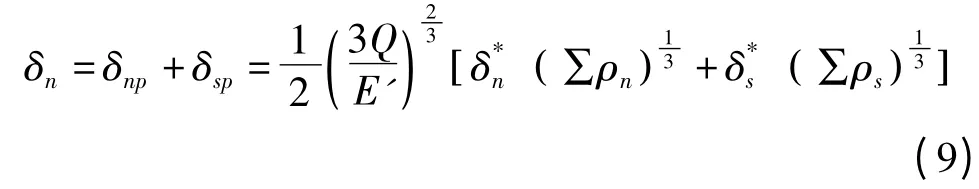
式中:δnp为滚珠与螺母滚道面的弹性接触变形量;δsp为滚珠与丝杠滚道面的弹性接触变形量;∑ρn为螺母侧滚道主曲率之和;∑ρs为丝杠侧滚道主曲率之和。

螺母滚道面与丝杠滚道面的法向弹性位移δn，会使得螺母相对于丝杠在轴线方向上产生轴向弹性变形量，设其值为δa，由图2 所示几何关系可得式(10)。

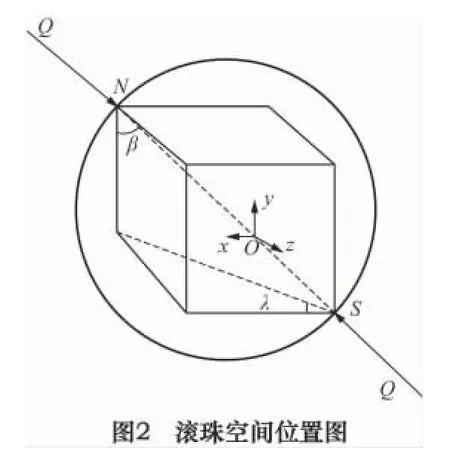
将式(8)、(9)代入式(10)，可得丝杠进给系统的载荷变形关系)

将式(11)两边对δa求导，可得丝杠进给系统的轴向刚度为

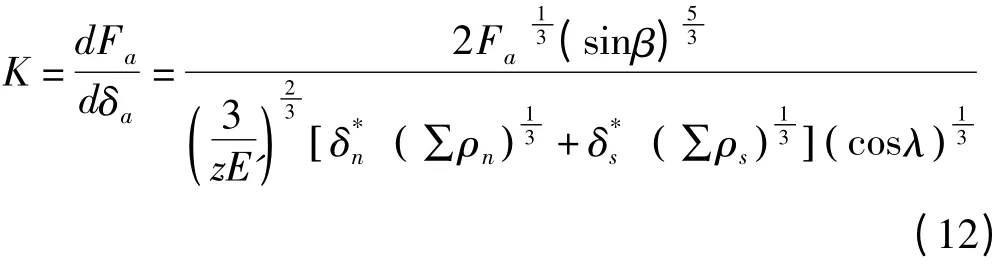
由式(12)可知，丝杠进给系统的轴向刚度受轴向载荷、接触角、螺旋升角、滚珠个数、主曲率和等因素的影响。丝杠进给系统在停顿和换向时，突然加载或卸载，都会产生轴向弹性变形，这就使滚珠丝杠的运动产生一定滞后，从而影响丝杠进给系统的定位精度。

3 丝杠进给系统轴向接触刚度的影响因素分析

3.1 轴向载荷

本文所用丝杠进给系统各部件的材料均为轴承钢，室温下其结构性能参数如表1 所示。

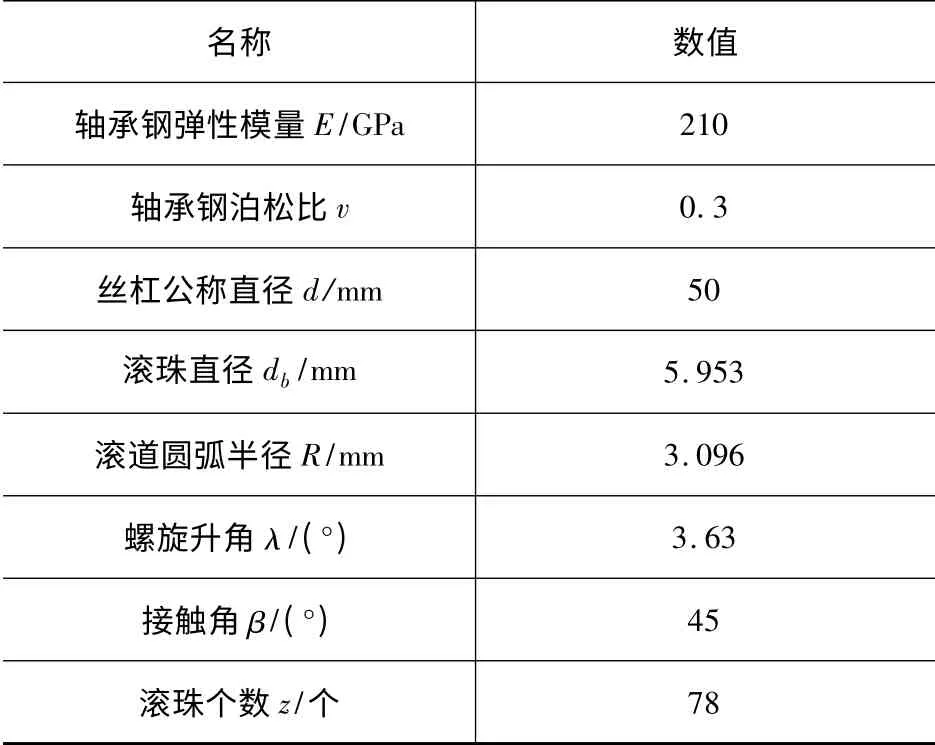
表1 丝杠进给系统结构性能参数

根据丝杠进给系统轴向刚度的计算公式，取轴向工作载荷为1 ～12 kN 之间。由式(12)计算得到不同接触角时丝杠进给系统轴向刚度与轴向载荷的关系曲线如图3 所示。

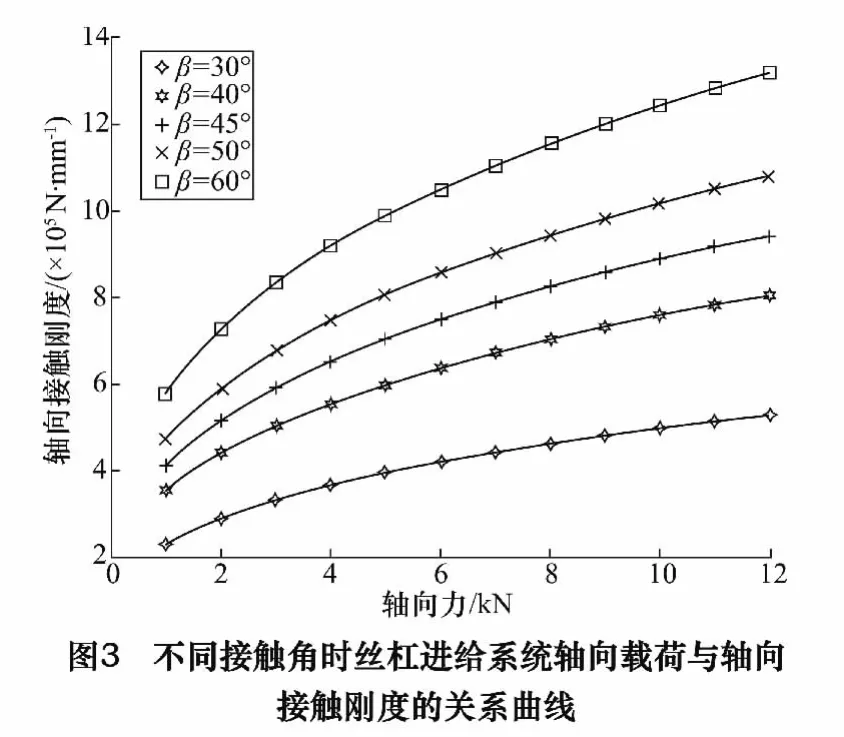
由图3 可以看出，丝杠进给系统的轴向刚度随着轴向载荷的增大而增大，并且轴向刚度随轴向载荷的变化呈非线性。

3.2 接触角

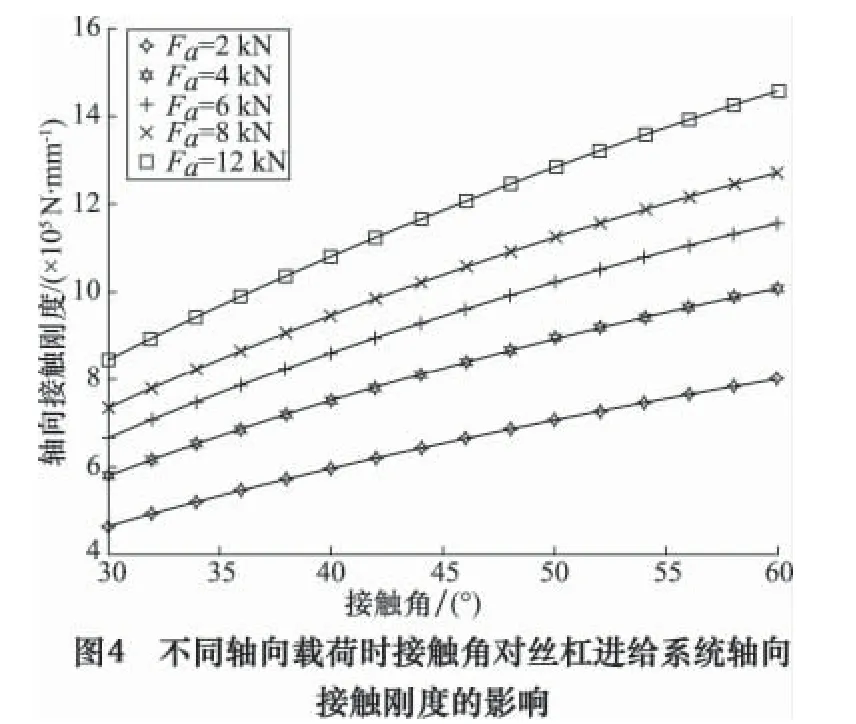
接触角是丝杠进给系统的重要结构设计参数之一。接触角对丝杠进给系统的传动性能影响很大。保持其他参数不变，丝杠进给系统的轴向载荷分别取2、4、6、8 和12 kN，接触角在30° ～60°变化时，接触角与丝杠进给系统轴向刚度的关系曲线如图4 所示。

由图4 可知，接触角在30° ～60°范围内变化时，丝杠进给系统的轴向接触刚度随接触角的增加而增大。但接触角越大，加工越困难，一般取标准接触角为45°。

3.3 滚珠个数

在一个螺母上具有独立运动的滚珠链数目称为列数。如果只有一条独立运动的滚珠链，称为单列;有两条则称为双列;两条以上则称为多列。工作滚珠数是指一条独立运动的滚珠链的滚珠数(即一列中的滚珠数)。通常一列中的工作滚珠数不超过150 颗。因为在一列中滚珠数越多，传动效率越低，运行阻力越大，尤其启动更困难，甚至导致阻滞，产生卡球现象。因此要限制工作滚珠数，其目的在于保持滚珠流畅性。

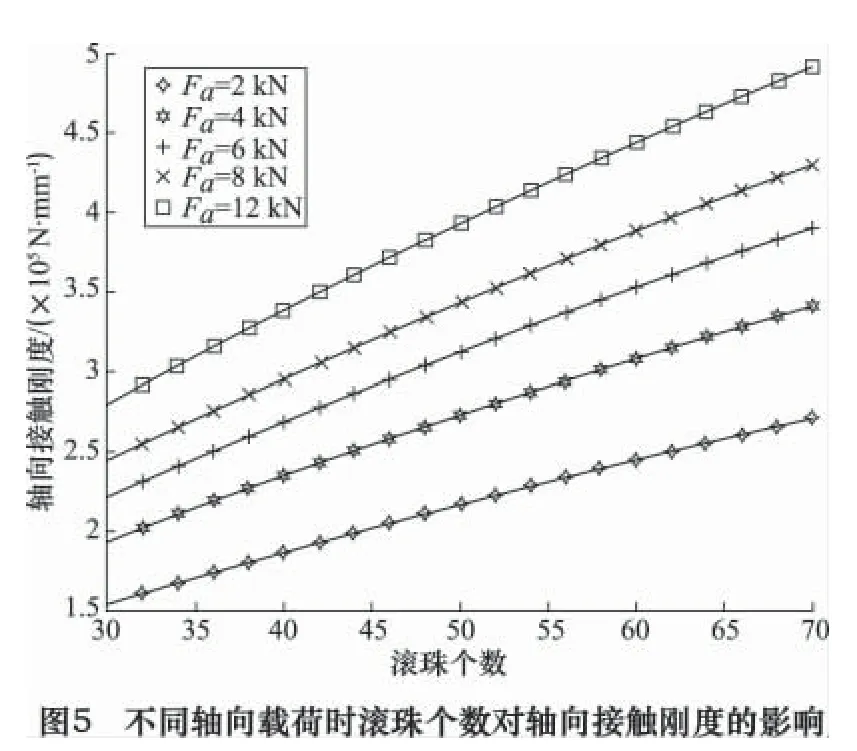
保持其他参数不变，丝杠进给系统的轴向载荷分别为2、4、6、8 和12 kN，滚珠个数在30 ～70 变化时，滚珠个数与丝杠进给系统轴向刚度的关系曲线如图5。

由图5 可知，丝杠进给系统的轴向接触刚度随滚珠个数的增加而增大，并且丝杠进给系统的轴向刚度与滚珠个数的变化关系接近线性。

3.4 螺旋升角

丝杠进给系统高速化，要求一方面提高丝杠轴的转速，另一方面增加丝杠进给系统的导程。增大导程就意味着增大丝杠进给系统的螺旋升角。螺旋升角增大，丝杠进给系统的性能就会发生变化，尤其是丝杠进给系统的轴向接触刚度。因此有必要研究螺旋升角对丝杠进给系统轴向接触刚度的影响。

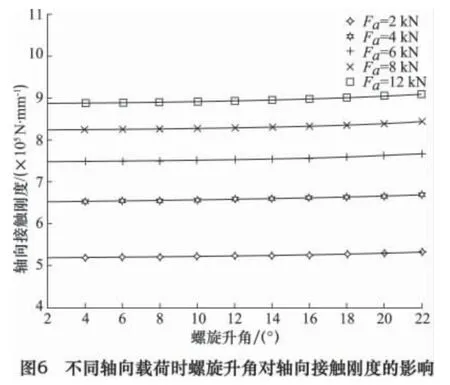
保持其他参数不变，丝杠进给系统的轴向载荷分别取2、4、6、8 和12 kN，螺旋升角在2° ～22°变化时，丝杠进给系统的螺旋升角对轴向刚度的影响如图6 所示。由图6 可知，丝杠进给系统的轴向接触刚度随螺旋升角的增加而增大，但增加幅度不明显。

3.5 滚道曲率比

丝杠进给系统中螺纹滚道圆弧半径与滚珠半径的比值称为滚道曲率比，滚道曲率比的大小对丝杠进给系统的传动承载能力有很大的影响。

保持其它参数不变，丝杠进给系统的轴向接触载荷分别为2、4、6、8 和12 kN，滚道曲率比在1.02 ～1.18 变化时，滚道曲率比对丝杠进给系统轴向接触刚度的影响如图7 所示。由图7 可知，丝杠进给系统的轴向接触刚度随滚道曲率比的增加而减小，并且丝杠进给系统的轴向接触刚度与滚道曲率比的变化关系呈非线性。

4 结语

本文利用赫兹接触理论建立了丝杠进给系统的轴向接触刚度模型，通过仿真实验分析了丝杠进给系统轴向接触刚度的影响因素。结果表明:丝杠进给系统轴向接触刚度随轴向载荷的增加而增大，并且轴向接触刚度随轴向载荷变化呈非线性;接触角在30° ～60°变化时，丝杠进给系统的轴向接触刚度随接触角的增加而增大;丝杠进给系统的轴向接触刚度随滚珠个数的增加而增大，并且丝杠进给系统的轴向刚度与滚珠个数的变化关系接近线性;丝杠进给系统的螺旋升角在2° ～22°变化时，丝杠进给系统轴向接触刚度随螺旋升角的增加而增大，但增大幅度不明显;丝杠进给系统轴向接触刚度随曲率比的增加而明显减小。

［1］Kim M S，Chung S C. A systematic approach to design high -performance feed drive systems［J］. International Journal of Machine Tools ＆Manufacture，2005，45(12):1421 -1435.

［2］Ebrahimi M，Whalley R. Analysis，modeling and simulation of stiffness in machine tool drives［J］. Computers ＆ Industrial Engineering，2000，38(1):93 -105.

［3］Zaeh M F，Oertli T. Finite element formulation of pre - stressed ball screw drives［C］. Proceedings of the 7th Biennial Conference on Engineering Systems Design and Analysis， Manchester， United Kingdom，2004.

［4］Maj R，Modica F ，Bianchi G. Machine tools mechatronic analysis［J］.Journal of Engineering Manufacture，2006，220:345 -353.

［5］Chen J S，Huang Y K，Cheng C C. Mechanical model and contouring analysis of high-speed ball-screw drive systems with compliance effect［J］. International Journal of Advanced Manufacturing Technology，2004，24(3):241 -250.

［6］Nakashima K，Takafuji K. Stiffness of a pre - loaded ball screw［J］.Transactions of the Japan Society of Mechanical Engineers，1987，53(492):1898 -1904.

［7］Harada H，Kagiwada T. Development of dimensional measurement and shape analysis system for ball screw［J］. Transactions of the Japan Society of Mechanical Engineers，1997，63(612):2911 -2917.

［8］蒋书运，祝书龙. 带滚珠丝杠副的直线导轨结合部动态刚度特性［J］. 机械工程学报，2010，46(1):92 -99.

［9］尹明. 两端固定支承的丝杠轴向刚度分析［J］. 精密制造与自动化，2007(3):32 -34.