洛必塔法则等极限方法的分析与研究

王 宁

（黄河水利职业技术学院，河南 开封475004）

极限是用来研究微积分学的工具，是沟通常量与变量、有限与无限的通道，是自始自终贯穿微积分学之中的一个重要推理工具；极限的计算是事物运动变化由量变到质变的辨证规律在数学上的反映.导数和积分的定义都是建立在极限的计算基础上的[1].通过求极限的过程来实现解决问题的思想方法是高等数学的精髓所在，因此，熟练掌握极限的计算是必须的，对于高等数学的系统学习是非常必要的.在极限运算中，选择何种方法十分重要，方法合适恰当，计算可以简捷快速，反之则有可能冗长繁琐，耗费时力，且易出错.通过对洛必塔法则、利用等价无穷小量替代法等函数极限若干计算方法分析研究，并经实例加以证明，总结出极限的计算规律和技巧.

1 利用两个重要极限求极限

在极限的计算中，许多重要结果是可以直接引用的，其中，两个重要极限及其变形技巧就是其中重要的内容，在计算的过程中灵活运用它们可以使极限求解变得简捷。这两个重要极限其实并不是常常能够直接运用，通常需要变形技巧，把所要求的极限变换或凑成如下直观的结构式[2]（即推广式）：

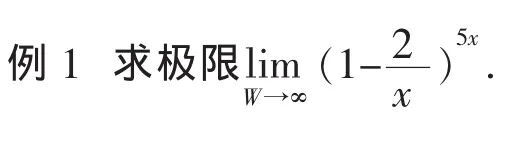
2 利用等价无穷小量替代法求极限

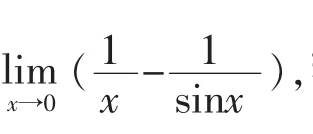
此解法答案虽然正确，但方法却是错误的.

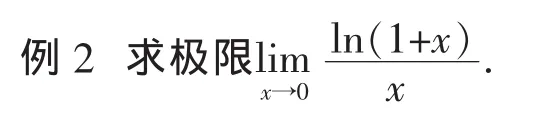
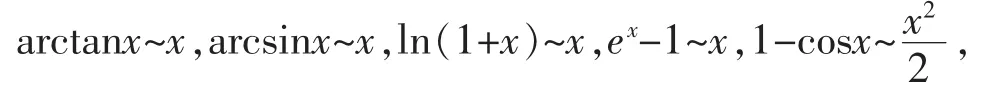
分析 对无穷无穷小量的代换，应该更深一层的理解，即当 x→0时，ln（1+x）～x可理解为当W→0时，ln（1+W）～W。其余类似，可以较快且能简便地求得极限。

3 利用函数的连续性求极限

4 利用洛必塔法则（L’Hospital）求极限

两个无穷小（大）量之比的极限可能存在，也可能不存在，因此把两个无穷小量或无穷大量之比的极限统称为不定式极限，分别记为型或型的不定式极限.它不能直接用商的极限运算法则计算.实际上，导数本身就是讨论型不定式极限，因此，就能够以导数为工具来研究一般不定式的极限.这种在一定条件下通过分子分母分别求导，再求极限来确定不定式的值的方法称为洛必塔法则（L’Hospital）.洛必塔法则提供了一种确定不定式极限的相当普遍且有效的方法.

对于“1∞”型、00型、∞0型，一般采用换底法将其化为“0·∞”型不定式（见下面阐述），再变形为型或型不定式，最后用洛必塔法则求解.

需要注意的是，洛必塔法则与其它求极限的方法，如恒等变形、等价无穷小代换法、重要极限法等融合使用，才可以更好发挥其作用，且在极限求解中应用较多，值得重视.以下举例说明：

分析 此题直接用洛必塔法则，那么分母的导数（尤其是高阶导数）较复杂，所以先用等价无穷小量替代：sin2x～x2则运算就简便多了，具体计算如下：

5 利用换底法求极限

幂指函数 f（x0）g（x）极限是极限计算的一个重要部分，通常采用先换底，换成以e为底的指数函数的形式，再求极限，即

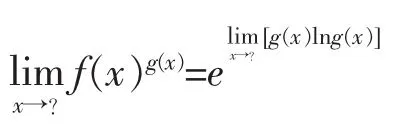
这种求幂指数极限的方法称为换底法.

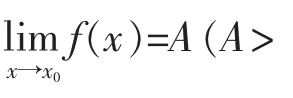
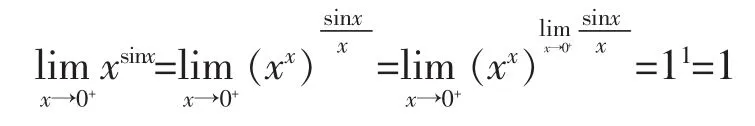
虽可求解，但难度偏大，更重要的是当A、B不是有限常数，或者A≤0，就不能通过计算底和指数的极限求出幂指函数的极限，例如对于“1∞”型、00型、∞0型不定式就是这样，所以这种解法有较大的局限性.相比之下，换底法具有普遍代表性.

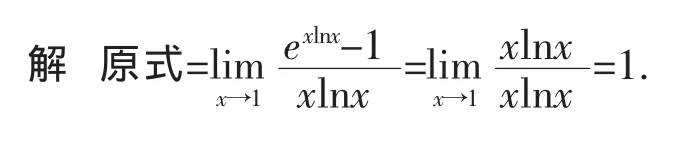
6 利用泰勒公式求极限

求不定式极限用洛必塔法则是很有效的，但是对某些问题并不方便甚至不能求出，此时可利用带余项的泰勒展开式加以解决，泰勒公式在对条件特殊的不定式极限计算时将发挥独特作用.在运用泰勒展开式展开函数的时候，要注意的是应当按照实际需要来展开到适当的项数，这样能使计算量相对减少.

除了以上介绍的方法外，还可以利用极限定义以及极限四则运算法则、中值定理等求解极限；利用夹逼准则或“无穷小量与有界变量的乘积是无穷小量”等性质求解；利用因式分解、通分、三角公式恒等变形、有理化法等多种极限方法求解[6].限于篇幅，本文不再赘述.

7 结语

解决极限问题的方法是众多的，对于同一个问题，可以有不同的求解方法，一种方法也可能用于几种题型，有时在一个题目中要用到几种方法融合求解.若遇到用某种方法不易或难于解决的问题，不妨换个角度、换种方法或可快速而准确地得到答案。极限求解具有多样性和复杂性的特点，因此对各种计算方法做到融会贯通，并有针对性地使用，才能方便高效地运用这些方法来解决问题.

[1]周世新.关于函数极限求法的探讨[J].呼伦贝尔学院学报，2009，17（1）：70-72.

[2]周明儒.高等数学[M].南京大学出版社，2005.

[3]孙玉梅.例谈极限问题的类型及解法[J].洛阳理工学院学报，2013，23（2）：89-92.

[4]宋砚求.极限的常用方法[J].内蒙古民族大学学报，2008，14（2）：4-5.

[5]吴顺唐.数学分析[M].南京：南京大学出版社，2005.

[6]王宁.基于MIS的数据库备份与恢复技术研究与实现[J].南阳理工学院学报，2012，7（4）：18-22.