用Matlab确定古塔中心点坐标的方法

王金生，桂承飞，王 晨

（金华职业技术学院，浙江 金华 321007）

古塔为重要文物，但由于受外力和坏境的影响，古塔可能会发生各种变形.为了保护古塔，便于修缮，文物部门需定期对古塔进行了观测，定量分析古塔倾斜、弯曲、扭曲等变形情况.其中古塔各层中心点坐标的确定对进一步研究古塔的变形尤为关键.目前，对古塔各层中心点坐标有一些求解方法，如：各点到中心点的距离的平方和最小的优化模型[1]、均匀多边形的重心坐标公式模型[2～3]、形心计算公式模型等.本文在此背景下，结合古塔或其他建筑物的测量方法和测量的实际情况[4～6]，用最小二乘法对每层数据点做平面拟合，对数据在平面上的投影点数据做椭圆拟合，最后将平面与直线的交点近似看作中心点进行求解，并将对缺失数据的情形进行讨论.

1 各层观测点的测量

1.1 平面监测基准网的建立

目前，观测点数据的采集可用地面三维激光扫描仪测量点云数据，通过对古塔进行三维建模[5]，用点云数据更全面和准确地定量分析古塔的各种变形.但也可以用传统的测量工具进行测量，其测量方法是在古塔院内四周选定几点稳定的位置，构成四边形或三角形，埋设采用六角钉等标志，并以南北方向的两个控制点所在直线向北为X轴正向，与这两点所在直线垂线往东向为Y轴正向，以其中一个控制点作为原点，建立独立直角坐标系，以该坐标系作为平面监测基准网[4].

1.2 观测点的选取及测量

古塔的横截面形状基本都是正多边形或圆，测量专业的文献和书籍[4，6]中提到观测点一般选取在多面体的侧棱与每层地平面的交点上，其选取的观测点数量与棱数相同，圆柱形的塔的观测点可以有更多.如果要选取观测点数量超过棱数，当然也可以，但这时需用形心的做法会更准确；如按上面的选取方法，本文的方法更为简单和准确.

由于某些原因，塔建造的位置较特殊，如塔建在悬崖边、海边、河边、湖边时，其一侧无法布设观测点，有时塔本身有残缺[4]而影响到常规的布设观测点.这些情况观测点只有一半或部分，这时若用形心的方法去做会有很大的误差，如用本文的方法可以解决此问题.

2 确定中心点的模型

2.1 模型分析

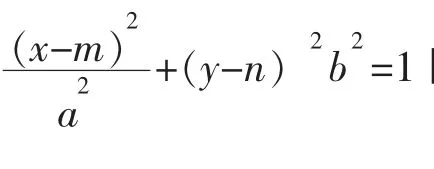
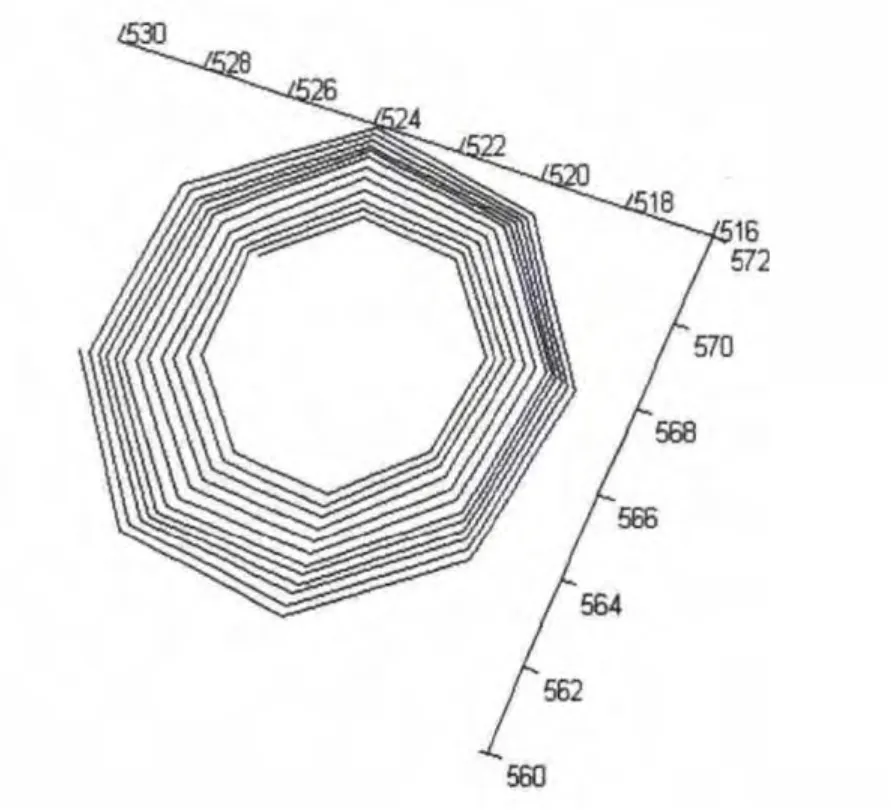
图1 附件1观测点散点图

图2 椭圆柱体中轴线与平面相交

2.2 建立模型

确定中心点坐标为：（m，n，Am+Bn+c）.

2.3 求解模型

案例一：以2013年全国大学生数学建模竞赛C题数据附件1为例，由于塔顶数据不全，现仅对13层的数据进行计算.先将附件1中的表头和数据之间的列都删去，把表变成104×12的纯数据工作表，用Matlab软件运行以下代码即可求得所有中心点坐标.

案例二：如受一些特殊因素（悬崖、海、河、湖等）影响，无法四周观测，在只有部分观测点数据的情况下，还是以附件1为例，将附件1中每层8个观测点数据去掉后面4个观测点数据，以上程序代码作如下修改即可求得所有中心点坐标.

第5行中104改为52、11和12行中j+7改为j+3、第 17 行中（j+7）/8 改为（j+3）/4.

2.4 模型的结果与分析

运行案例一和案例二的程序，部分结果见表1，对附件1中的第一次观测数据每一层统计出8个点各个坐标的最值，发现表1中每一层中心点坐标均没有超出这个最值范围，并与文献[1～3]、［7～8]的研究结果进行比较，近似度很高.对比4个观测点和8个观测点的结果发现，两者之间有一定的误差，其主要原因是数据缺失较多，拟合的椭圆的圆心误差会较大，因此，通常情况建议用完整的数据点，如案例一中，其误差会很小，但对于特殊情况用案例二的方法解决一些残缺数据的拟合，虽有误差，但也可以为后续的进一步研究提供参考.

表1 第一次观测两案例每层中心点坐标

3 模型评价和改进

应用以上模型求解中心点坐标，与其他文献的求解方法相比有较高的准确性和简便性.用该模型求得的结果可以给古塔的变形研究提供可靠的数据支持，在此基础上得到的倾斜、弯曲、扭曲等变形的定量分析更为细致和准确.该模型对观测点的要求比较高，要选取侧棱上的观测点才较为准确，不像形心的计算方法，选取观测点可以随意些；而且还能解决在缺失观测点数据情况下的问题，缺失数据较多时拟合出的结果误差会比较大.其实附件1中有缺失数据，若用本文方法，可以不用补全数据即可求出中心点.平方和最小的优化模型[1]认为中心点即与四周距离相等的点，根据各层实际观测点近似对称地分布在一个平面的特征，在所求得的各层拟合平面中寻找一点，使其到该层各观测点距离的平方和最小，建立如下优化模型：

目标函数：到该层各观测点距离的平方和最小，即

表2 案例一第一次测量中心点坐标

约束条件：该中心点在拟合平面上，即

用Matlab程序求得案例一中的结果见表2

虽然从结果比较，差别在千分位上，但是两种模型的计算方法有本质的区别，不管从难易程度还是精确度比较，本文模型更为简洁，计算更为方便，且结果更精确.

该模型还可以应用于有对称结构的建筑物，通过观察点的数据，利用本文方法可以求得建筑物每层的中心点，给建筑物三维建模提供一些内部数据.

[1]肖渝琳，刘新燕，黄龙.古塔的变形——2013年数学建模C优秀论文[EB/OL].（2013-12-09）.http：//www.doc88.com/p-9753784873471.html.

[2]贺永会.古塔变形的预测模型[J].人工智能及识别技术，2013（22）：91-92.

[3]柴守立.基于Matlab的古塔变形分析与预测 [J].人工智能及识别技术，2013（24）：79-80.

[4]黄强.古塔变形监测的探讨[J].测绘与空间地理信息，2013，6（6）：217-220.

[5]谭仁春.三维城市模型的研究现状综述[J].城市勘测，2007（3）：24-54.

[6]顾孝烈，鲍峰，程效军.测量学 [M].上海：同济大学出版社：3版，2006.

[7]童强，文晖.一种古塔变形的定量分析方法[J].兰州石化职业技术学院学报，2013，9（3）：29-31.

[8]王锦升，杨伟芳，邹德玉.利用曲线拟合分析古塔的变形[J].价值工程，2013：254-256.