电厂主汽温的模糊逆控制

孙灵芳，赵瑞，麻世博

（东北电力大学自动化工程学院，吉林吉林 132012）

当过程控制系统存在较大纯迟延环节［1］时，会使系统的闭环特征方程式包含纯迟延因子，这就必然导致系统的稳定性降低.特别是当迟延时间足够长时，还可能造成系统的不稳定.这就是大迟延过程难以控制的本质.因此，大迟延对象的控制方法一直是控制理论研究的重要课题.

目前，逆动力学的研究已经在许多领域取得了进展，如在电动机控制、［2］船舶、［3］导弹控制［4］及热力系统［5］中均有应用.逆控制是指用被控对象逆动力学模型的输出作为控制量去驱动该被控对象，以使整体构成一个伪“1”的系统，使得控制系统的输出能够跟随控制指令.

为了解决迟延环节对电厂主汽温系统的影响，本文将逆动力学与模糊理论相结合，仿真结果表明，本文采用的方法具有良好的抗干扰性和鲁棒性.

1 逆动力学过程模糊辨识

1.1 T-S逆模糊规则

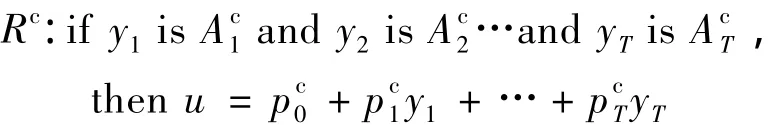
式中：y1，y2，y3，…，yT——前件变量;

u——输出;

p0，p1，p2，…，pT——后件参数.

1.2 前提参数的辨识

本文采用模糊C-均值聚类算法来确定逆模型前提变量空间的最优划分及最佳前提参数.具体步骤如下.

（1）初始化各参数.定义初始聚类数目c，加权因数m（m=2），样本个数N;初始化隶属度矩阵U，参照模糊C-均值聚类算法（Fuzzy C-means Algorithm，FCM）的步骤对样本数据进行聚类，得到c个聚类中心值.设定迭代停止阈值ε（一般取0.001～0.01），设置迭代计数次数l，初始化聚类原型V（l）（l=0）.

（2）更新模糊划分矩阵：

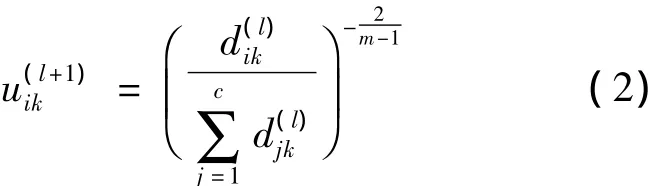
（3）计算新的聚类中心矩阵：

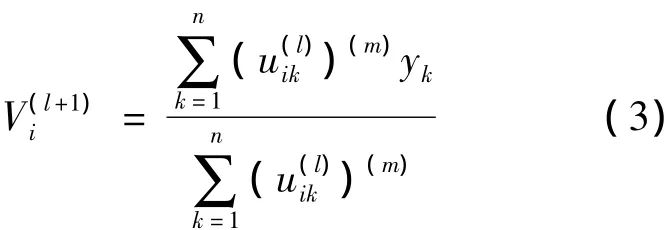
（4）判定阈值.根据给定的阈值ε，如果‖V（l+1）-V（l）‖≤ε，则停止迭代，否则l=l+1，转至步骤（2）.

1.3 结论参数的辨识

本文采用最小二乘法来辨识结论参数.若对N组数据作聚类分析所得规则数目为c，则根据模糊规则可得模糊输出为：

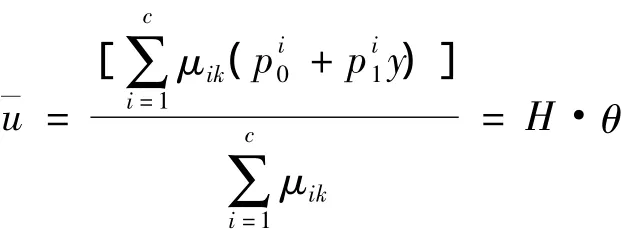
具体步骤如下.

（1）对给定的主汽温系统数据样本进行计算：

（2）初始化参数θ0=0，S0=αI.其中，α为较大整数，取α=105，I为单位阵.

（3）计算：

式中：Mk——增益向量;

Sk——协方差矩阵;

θk——待辨识的参数向量;

Hk——数据行向量.

（4）k+1→k，如果k≤L，返回步骤（3）;否则，递推完毕.

最后，计算性能指标：

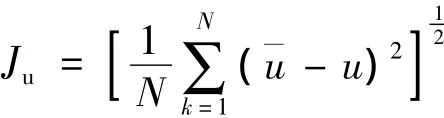
如果Ju达到辨识精度的要求或Ju下降的趋势变缓慢，则结束，否则继续迭代.

1.4 T-S模糊逆模型的验证结果

现以华能某300 MW机组的主汽温系统为例，取250组输入和输出数据（输入为减温水流量u，输出为电厂主汽温y），采样时间t=1 s.当模糊聚类数不同时，逆模型的辨识结果和辨识误差如图1至图3所示.

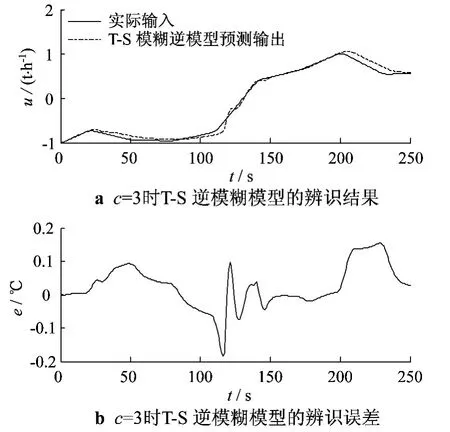
图1 c=3时T-S逆模型的辨识结果及辨识误差

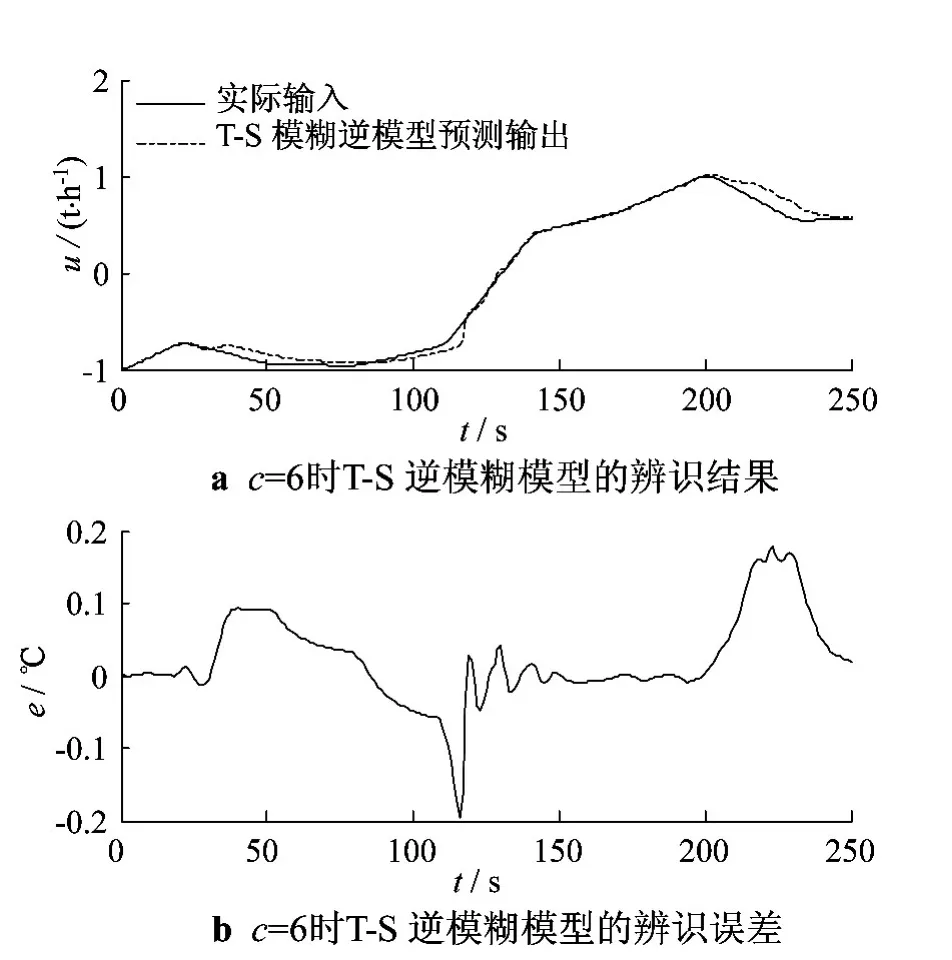
图2 c=6时T-S逆模型的辨识结果及辨识误差

图3 c=20时T-S逆模型的辨识结果及辨识误差

不同聚类数目c下的性能指标Ju见表1.

表1 逆模型不同聚类数目c下的性能指标J u

由模糊逆模型结果分析可知，随着聚类数目c的增加，性能指标Ju越来越小，残差越来越小，即辨识精度越来越高.当c=6时，模糊模型的精度和复杂程度均已满足要求.

2 T-S模糊逆控制器的设计

本文根据系统输出误差，采用自适应滤波算法在线调节T-S模糊逆控制器的参数.本文的控制思想是：通过模糊辨识理论建立模糊逆模型，作用到被控对象上，将迟延量与系统输出比较得出的误差作为训练信号，采用最小均方根（Least Mean Squares，LMS）算法在线调节T-S模糊逆模型的参数.

控制系统总体结构如图4所示.

图4 控制系统总体结构示意

2.1 迟延量的辨识

为了得到理想的控制效果，在迟延量的决策过程中，本文以采用相关性分析法获得u（t）的最大相关量为参考依据.

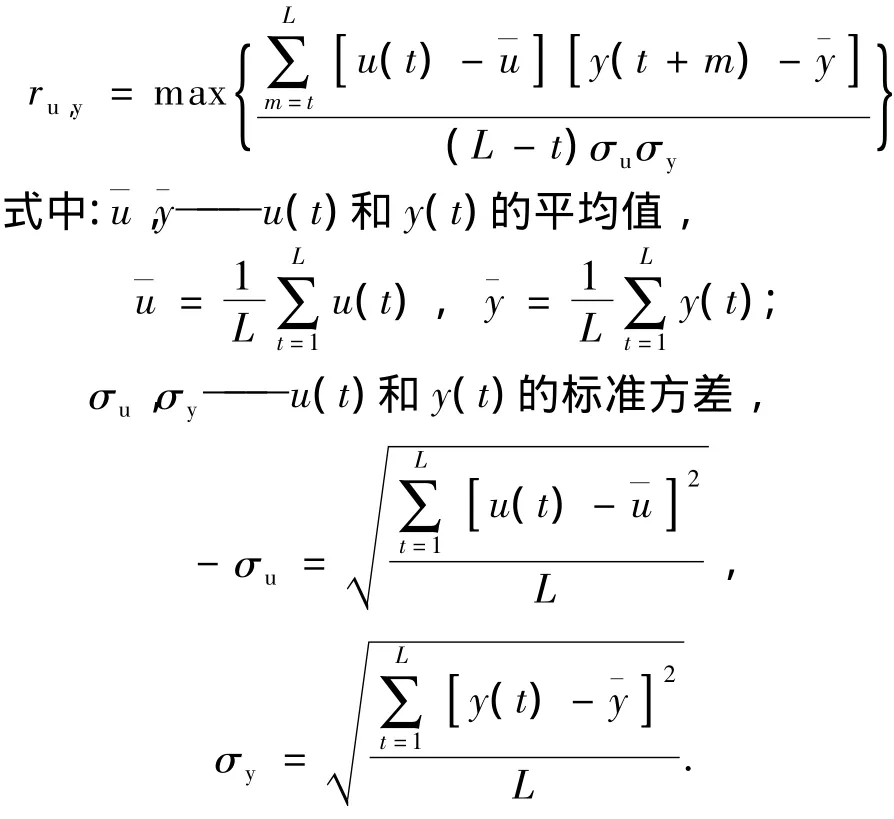
当ru，y取得最大值时，延迟量等于m.

2.2 LMS滤波算法

考虑图5所示的线性组合器，其输出信号是所有输入信号的线性组合，即：

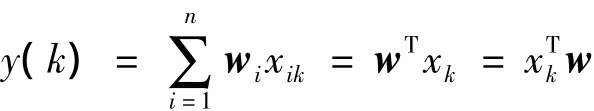
式中：xk——输入信号，xk=［x1k，x2k，x3k，…，xnk］;

w——权系数向量，w=［w1，w2，w3，…，wn］.

由LMS算法可知，权系数w的更新公式为：

式中：μ——步长收敛因子.

将LMS算法用于在线调节逆模糊模型结论参数p，即p作为该算法中所要调节的权值，其更新公式为：?

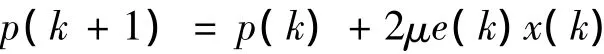
图5 自适应线性组合器

3 T-S模糊逆控制在大时滞系统中的应用

笔者发现逆系统阶跃输出响应曲线中存在一定动态误差，因此引入PID补偿环节.以某电厂300 MW锅炉过热汽温某一负荷下的主汽温模型为例，进行控制仿真.

在串级系统中模型描述如下：

（1）惰性区

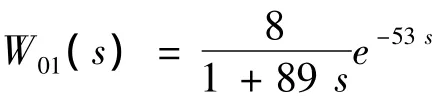
（2）导前区

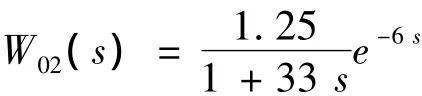
整个系统可以描述为一个二阶惯性环节加纯滞后，即：

3.1 单位阶跃输入试验

T-S模糊逆控制系统与传统串级控制系统输出曲线比较如图6所示.

从图6中可以看出，传统的串级控制系统调节时间长约500 s，T-S模糊逆控制系统输出无超调，调节时间短，约为300 s，并且带PID补偿的逆控制系统比直接逆控制系统更加稳定.

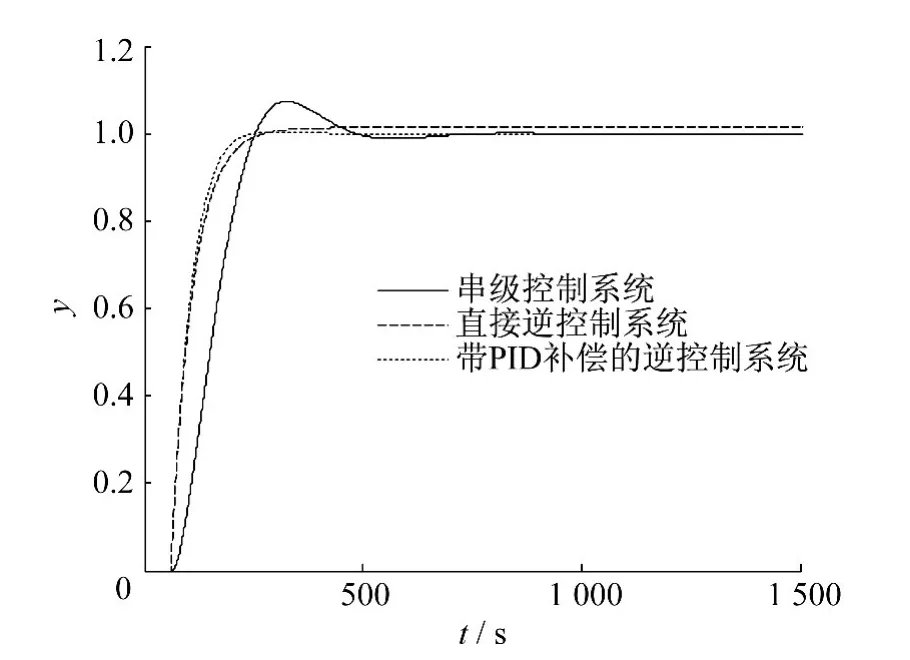
图6 单位阶跃输入时3种系统输出曲线对比

3.2 鲁棒性试验

为了再次验证控制系统的有效性，在第1 000 s时加入0.1的阶跃扰动，观察串级控制系统、直接逆控制系统、带PID补偿的逆控制系统这3种系统的扰动响应，如图7所示.由于直接逆系统是开环控制，产生扰动无法消除，而加入PI补偿的模糊逆系统的输出反应速度快，产生的扰动超调也相应变小.相比之下，当扰动出现时，串级系统的超调量较大，且调节时间相对较长.

图7 加入阶跃扰动时3种控制系统扰动响应曲线比较

3.3 动态性能试验

实际中锅炉汽温对象在不同的运行工况下对象的特性容易发生非常明显的变化，而且主汽温对象的变化主要在惰性区.为考察逆系统的适应能力，本文假定惰性区的时间常数从89 s变为200 s，3种控制系统的输出曲线比较如图8所示.

图8 惰性区时间常数改变时3种控制系统输出曲线比较

4 结语

本文采用的自适应逆控制系统实现了电厂主汽温系统的快速稳定，而且能够克服系统的外在扰动;当对象参数发生变化时，系统也能较稳定地输出，不会发生较大的超调或震荡，具有较好的鲁棒性，优于传统的控制算法.

［1］潘峰，韩如成.时变大时滞系统的控制方案综述［J］.仪器仪表学报，2002，23（3）：789-790.

［2］刘坤，汪木兰，张新良.非线性伺服电动机的神经网络逆控制［J］.计算机仿真，2007，24（10）：152-155.

［3］赵隽，战兴群，张炎华.基于自适应逆控制技术的船舶操纵仿真控制［J］.上海交通大学学报，2003，37（8）：1 168-1 171.

［4］赵国荣，瞿军，李善高.导弹运动方程的逆解析解［J］.飞行力学，2000，18（3）：35-37.

［5］王广军，邓良才，陈红，等.锅炉汽温对象逆动力学过程模糊辨识［J］.中国电机工程学报，2007，27（20）：76-80.

（编辑胡小萍）