基于高斯核函数离轴数字全息零级像的抑制
张洪科,汤春明,于 翔,刘玉翠
(1.哈尔滨工程大学信息与通信工程学院,黑龙江哈尔滨 150001; 2.天津工业大学电子与信息工程学院,天津 300387;3.天津工业大学工程教学实习训练中心,天津 300387)
基于高斯核函数离轴数字全息零级像的抑制
张洪科1,汤春明2,于 翔3,刘玉翠1
(1.哈尔滨工程大学信息与通信工程学院,黑龙江哈尔滨 150001; 2.天津工业大学电子与信息工程学院,天津 300387;3.天津工业大学工程教学实习训练中心,天津 300387)
为了降低离轴数字全息的再现像中零级像对再现像的干扰,提出了一种利用高斯核函数在空域对数字全息图进行低通滤波,再用原数字全息图减去滤波后的全息图来抑制零级像的方法。实验结果表明空域高斯核函数处理法能有效地抑制零级像。把该方法与现有的频域法、减全息图均值法以及减局部均值法在抑制零级像的效果和计算速度上进行了比较,证明了该方法抑制零级像的效果好,计算速度快。通过所采用的方法提高了离轴数字全息再现像的质量。
数字全息;零级像抑制;高斯核函数;再现像
1 引 言
数字全息技术随着CCD性能的提高和计算机运算速度的加快,已经取得了明显的进步。如今,它已被广泛应用于科学实践中。例如,无损形变检测[1]和微结构测量[2]。离轴全息术能将实像、共轭像和零级像在空间分离,使它们之间互不干扰,因此而被广泛研究。但在再现时,共轭像和零级像会对再现像形成干扰。尤其是零级像,它占据了大部分的衍射能量。文献[3]指出,物光波和参考波在光强相等的情况下,真实像和共轭像能量分别仅占总衍射能量的1/6,零级像则占据4/6。所以,数字再现时零级像的抑制对再现像的质量的好坏有着极其重要的影响。目前,零级像的抑制主要从两方面进行研究:一是通过实验的方法来抑制零级像。如一步和两步相移法[4]。但是该方法至少需要记录下来两幅全息图,在记录时需要花费时间调节实验装置,这样只能适用于静态测量,不适用于动态测量。二是采用数字图像处理技术。该方法一般是从空域和频域对全息图进行预处理达到抑制零级像干扰的目的。在频域上处理[5],需要正反傅里叶变换,处理时间较慢。在空域上处理,只需记录一幅全息图,计算起来用时短,适合于在动态测量中的应用。空域局部均值[6]在抑制零级像时,在模板较大的情况下,零级像很难完全消除;全息图减去其均值法在有些时候抑制零级像的效果较差。
针对上述问题,本文提出利用高斯核函数的低通特性来抑制数字全息零级像的方法。文中在第二部分给出了该方法的理论分析,第三部分给出计算机模拟和实验的结果,并与现有的算法进行了比较。第四部分得出结论。
2 理论分析
2.1 离轴数字全息原理
离轴全息图在记录时物光和参考光需要满足一定的角度,使衍射再现时实像、共轭像和零级像互不干扰。定义x0y0是与物体相切的平面,xy是CCD所在的平面,xiyi是再现像所在的平面。三个平面之间的距离分别z0和zi,参考光选择波长为λ的平面波。O(x,y)是物平面光波的复振幅经距离z0的衍射到达CCD平面的光波的复振幅分布,R(x,y)是参考光在CCD平面的复振幅分布,则CCD记录下的全息图强度Ih(x,y)分布如公式(1)所示:
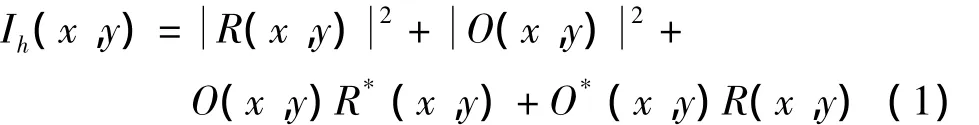
公式(1)的前两项合称为零级像,后两项分别是实像和共轭像。对公式(1)做傅里叶变换可以得到它的频谱分布。离轴数字全息的频谱分布特点如图1所示,中间低频是零级像的频谱,两边高频是实像和共轭像的频谱。离轴数字全息的再现是用参考光照射CCD记录下来的全息图,然后利用菲涅耳衍射积分进行计算。再现面的光波的复振幅I(xi,yi)分布如公式(2)所示:
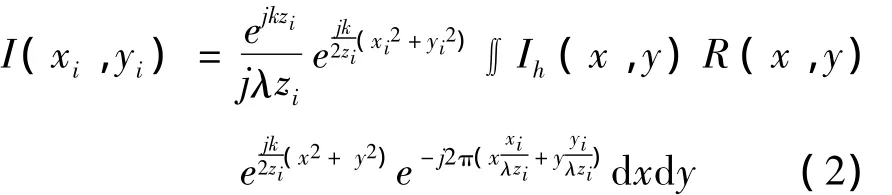
其中,k=2π/λ。
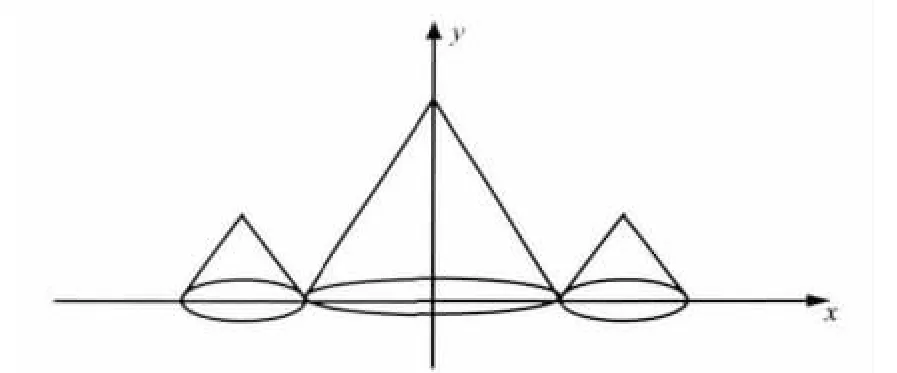
图1 离轴数字全息频谱分布示意图
2.2 高斯核函数抑制零级像原理
高斯核函数是一种常用的径向基函数。二维高斯核函数定义如公式(3)所示:
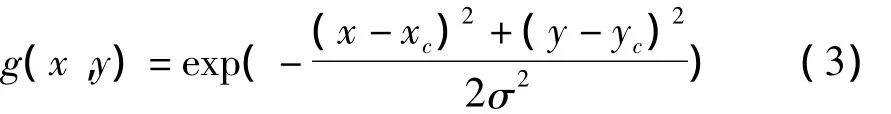
式中,σ控制函数的幅度;xc,yc是图像中心坐标值。二维高斯函数的频谱具有对称性和低通性,与离轴数字全息图做卷积运算后可以保留零级像,这样公式(1)中的后两项会被抑制,最后得到只含低频信息的前两项。在此基础上,用原全息图Ih(x,y)减去高斯核函数空域滤波后的全息图结果记为If(x,y),这样对If(x,y)进行菲涅耳再现时零级像就会被抑制。
在图像处理中,高斯滤波一般有两种实现方式,一是用离散化窗口滑窗卷积,另一种通过傅里叶变换。由于高斯函数可以写成可分离的形式,因此可以采用离散化窗口滑窗卷积,即可以把多维的卷积化成多个一维卷积。具体到二维的高斯滤波,就是指先对行做一维卷积,再对列做一维卷积。这样就可以将计算复杂度从 O ( M×M×N×N)降到O (2×M×M×N),提高计算效率,M,N分别是图像和滤波器的窗口大小。
3 实验结果及分析
为证明上述研究结果,我们采用了计算机模拟和实验获得的全息图进行研究。模拟研究的相关参数选择如下:波长λ=532 nm,CCD面阵宽度L= 4.76 mm,取样数1024×1024,物体的宽度 D0= 40 mm的“物”字图像,令记录距离z0和再现距离zi为1500 mm。图2给出了模拟研究的结果,从图2 (c)中看出,利用高斯核函数处理后的全息图再现时零级像得到明显抑制。
σ的大小影响着零级像抑制的效果。当σ取大时,高斯核函数的幅度小,抑制了低频信息幅度,在用原全息图减去滤波后的全息图,原全息图中零级像减少的幅度就少,从而受到较小程度的抑制;反之,当σ取小时,零级像将受到较大程度上的抑制。从图3中可以看出,随着σ的增大,零级像的抑制效果逐渐变差。所以,高斯核函数参数σ不宜选择过大,否则抑制效果较差。

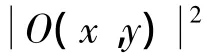
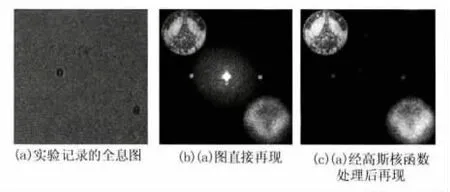
图4 实验记录的全息图直接再现和高斯核函数处理后再现
为作对比研究,图5分别给出了用频域法、全息图减去其均值法以及全息图减局部均值对实验记录的全息图处理后的再现结果。从图5中可以看出频域法、减全息图均值法以及减局部均值法较高斯核函数空域卷积法抑制零级像效果差。在双核CPU处理频率是2.8 GHz,内存2 GB的计算机仿真得到如下仿真时间:高斯核函数空域抑制法抑制零级像用时0.61 s,频域高斯高通滤波抑制法用时2.18 s,减全息图均值抑制法用时0.07 s,空域减局部均值抑制法用时1.01 s。虽然减全息图均值抑制法用时比本文方法短0.54 s,但抑制零级像的效果比本文的方法要差很多。
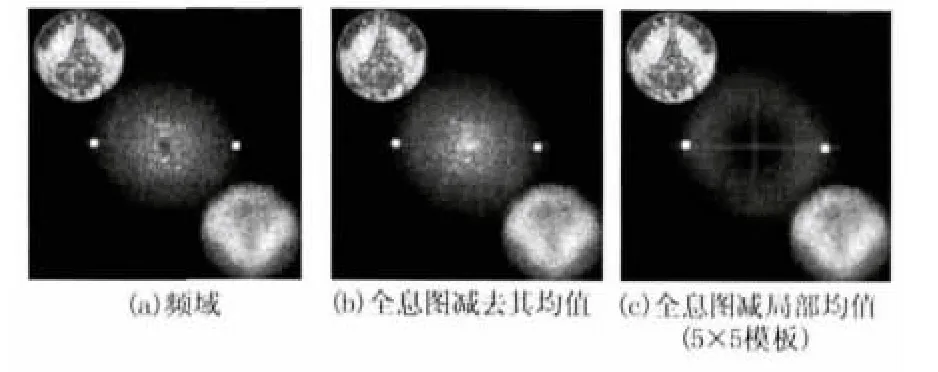
图5 不同算法抑制零级像的比较
4 结论
本文提出了一种基于高斯核函数在空域抑制离轴数字全息再现像中零级像的方法。该方法只需记录一幅数字全息图,在空域中进行低通滤波,再用原数字全息图减去滤波后的全息图来抑制零级像,零级像得到了有效地抑制,提高了离轴数字全息再现像的质量,处理时间较快,并且比频域高通滤波、全息图减去其均值和全息图减局部均值法抑制零级像的效果更好,适合用于动态实时测量,但是参数σ的选取不宜过大,否则会造成零级像抑制效果差。
[1]Xiong Juan,Kong Yinchang,Shao Mingshen.Objects deformation measurementbased on holographic double exposure[J].Journal of Optoelectronics,Laser& Infrared,2012,42(1):94-99.(in Chinese)
熊娟,孔银昌,邵明省.基于全息二次曝光的物体形变测量[J].激光与红外,2012,42(1):94-99.
[2]PR Hobson,JJNebrensky,ID Reid.Challenges in using GPUs for the real-time reconstruction of digital hologram images[C].Iopscience,2013.
[3]Xiong Bingheng,Li Junchang.Holographic interferometry: principles and methods[J].Beijing:Science Press,2009,570-571.(in Chinese)
熊秉衡,李俊昌.全息干涉计量—原理和方法[M].北京:科学出版,2009.
[4]Hou Ruining,Yan Youfang.Elimination method of zeroorder image and conjugate image of off-axis digital hologram[J].Laser Technology,2012,36(5):632-635.(in Chinese)
侯瑞宁,闰友房.离轴数字全息零级像和共轭像的消除方法[J].激光技术,2012,36(5):632-635.
[5]Yang Yong,Xue Dongxu,Ge Qi,et al.Suppression of zero-order image in off-axis digital holography based on homomorphic filtering[J].Optics and Precision Engineering,2012,20(9):1878-1882.(in Chinese)
杨勇,薛东旭,盖琦,等.同态滤波法抑制离轴数字全息零级项[J].光学 精密工程,2012,20(9): 1878-1882.
[6]Zhu Yuliang,Zhou Hao,Gu Jihua.A pre-processmethod based on spatial filter for zero-order image elimination in digital off-axis holography[J].Laser&Infrared,2010,40 (7):795-798.(in Chinese)
朱余良,周皓,顾济华.离轴数字全息零级像的空域滤波预处理消除法[J].激光与红外,2010,40(7): 795-798.
[7]Joseph W Goodman,Qin Kecheng,Liu Peisen,et al.Transl.Introduction to fourier optics[M].3rd.ed.Beijing:Publishing House of Electronic Industry,2011.(in Chinese)
Joseph W Goodman.傅里叶光学导论[M].秦克诚,刘培森,等译.3版.北京:电子工业出版社,2011.
[8]Li Junchang,Xiong Bingheng,et al.Information optics tutorial[M].Beijing:Science Press,2011.(in Chinese)
李俊昌,熊秉衡,等.信息光学教程[M].北京:科学出版社,2011.
Suppression of the zero-order image in digital off-axis holography based on Gaussian kernel function
ZHANG Hong-ke1,TANG Chun-ming2,YU Xiang3,LIU Yu-cui1
(1.College of Information and Communication Engineering,Harbin Engineering University,Harbin 150001,China;
2.College of Electronic and Information Engineering,Tianjin Polytechnic University,Tianjin 300387,China;
3.Engineering Teaching Training Center,Tianjin Polytechnic University,Tianjin 300387,China)
A new method to suppress the zero-order image by processing digital hologram with Gaussian kernel function in spatial domain is proposed.First,an original hologram is filtered by Gaussian kernel function.Then,the original hologram decreases the filtered hologram to suppress the zero-order image.It is correct and effective to suppress the zero-order image by experiment.Compared with themethods of the hologram subtracts itsmean,the hologram subtracts its localmean and frequency domain,the new method has a better and faster effect.The proposed method improves the quality of digital off-axis holography reconstructed image.
digital holography;suppression of zero-order image;Gaussian kernel function;reconstructed image
TN26
A
10.3969/j.issn.1001-5078.2014.01.020
1001-5078(2014)01-0090-04
张洪科(1987-),男,硕士,主要从事非线性信号与图像处理方面的研究。E-mail:zhk.721.521@163.com
2013-05-21

